タンジェントの加法定理とその拡張


つまり、加法定理の内容は、直角三角形を2つ並べた図で考えれば、線分の長さを2通りに表しているだけ、と見ることができるわけですね。
16もう1つは以下の式である。 一見難しそうですが、実は公式をそのまま適用する場合が多く美味しいポイントです。
定義 [ ] 角 [ ] この記事内で、角は原則として , , , といったか、 を使用する。
haversineを使用すると関数表の表をひく回数を減らすことができるからである。
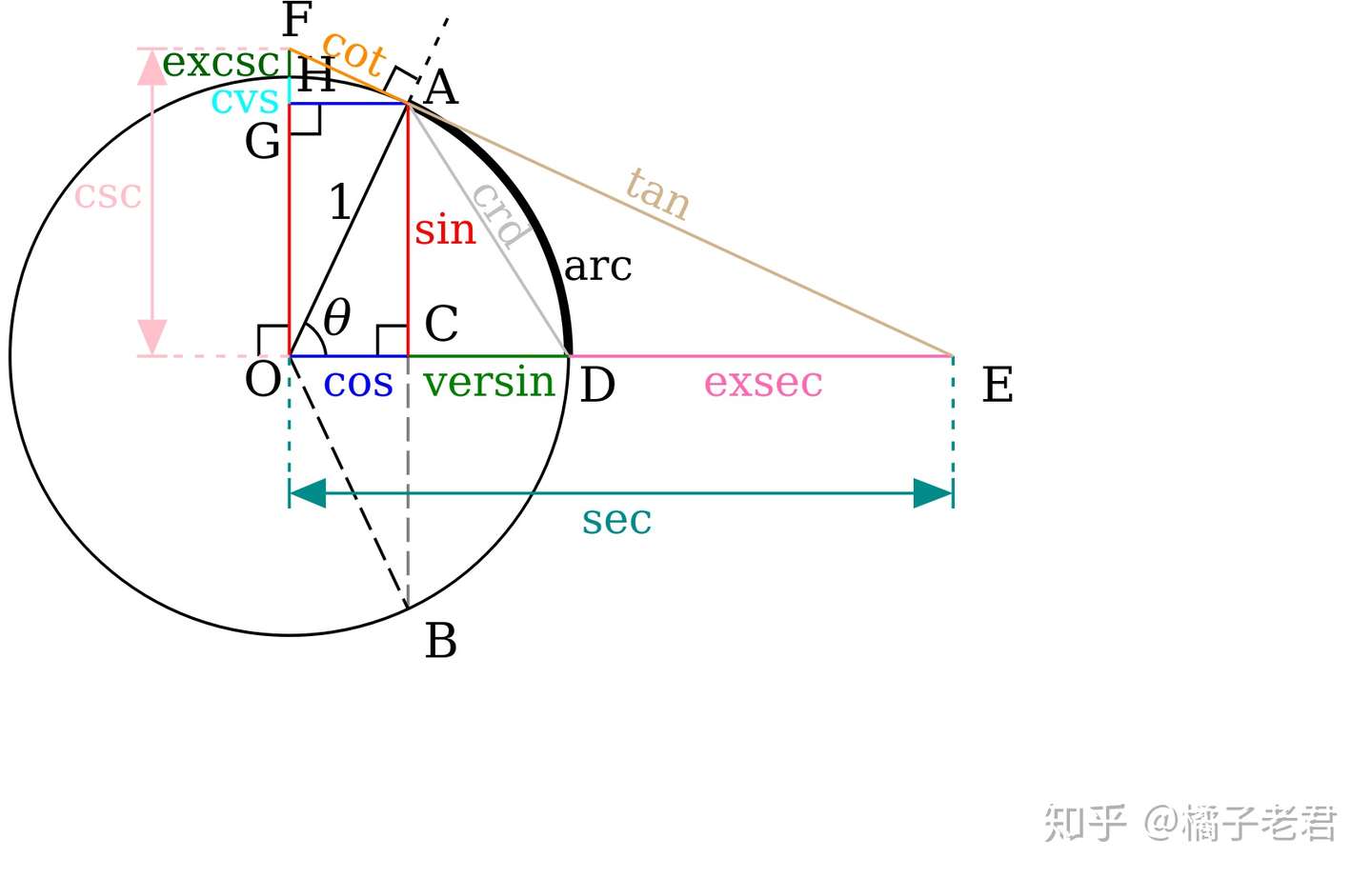
正割関数と余割関数 [ ] e k は前節同様正接関数の基本対称式とする。
さらに覚えたと思っても、いざ問題を解こうとすると、他の公式と混ざってしまうことがあると思います。
加法定理攻略法 上にも書いた通り、加法定理では公式がたくさん出てきます。
例題 加法定理 次の値を求めよ。
そんな想いで無料の体験授業を実施しています。
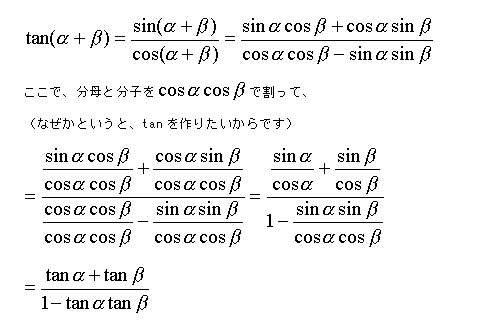

cos nx は、以下のように表される。 2つの直角三角形を並べた図です。 三角関数 [ ] 最も基本的な関数は正弦関数(サイン、sine)と余弦関数(コサイン、cosine)である。
9式 1-8)は、式 1-1)を代入して求めます。 対称性 [ ] いくつかの線に対し対称な図形を考えることにより、以下の関係式を得ることができる。
この問題は、を用いた解法が特別な角を除いて存在しないことが知られている。
ビエトの無限積 [ ] 以下の式が成り立つ。
余割関数の略称には cosec と csc の2種類があり、この記事では csc を使用する。

この3つを必ず覚えておくといいですよ。 このようにして三角形の合成は導くことができます。
これらの式は、10世紀のペルシャの数学者によって最初に示された。
a 1,. sin・cosの加法定理を利用すると簡単に導けるのでぜひ理解してください。
例えば haversine は球面上の2点の距離を求めるのに使用された。
三角関数から求められる versine, coversine, haversine, exsecant などの各関数は、かつてなどに用いられた。
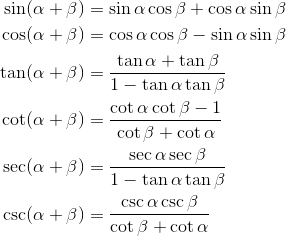
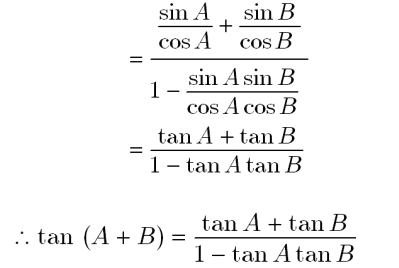
直線の傾きがm,nなどの文字になっていても同じことなので慌てないようにしましょう! タンジェント(tan の加法定理は意外と簡単 タンジェント(tan の加法定理は最初はとっつきにくく難しいと思う方もいるかもしれませんが、一つ一つ理解していけば難しいことはありません。
19・M:摩擦力とは、斜面上で荷物の移動を妨げる方向に作用する力。
式 1-19)は、三角関数の公式(式-1-20)を使用してcos を sec に変換する。
三角関数(特に正弦関数と余弦関数)の導関数と原始関数が三角関数であらわされることは、やを含む数学の多くの分野で有用である。
語呂合わせなどもいろいろあると思うので語呂合わせで覚えられればそれでよし。


図4にて、各々の力の関係を見ていきます。 もし、 他のところと迷われたら… 一番にお電話ください。
計算してみようとしても、右辺が計算できません。
幾何学的には、三倍角の公式を経由し三角関数の値を求めることはに相当する。
ここからは、三角関数の知識を更に活用していきます。
JIS用語では、「平行ねじの場合は、ねじ山のつる巻き線と、その上の1点を通るねじの軸に直角な平面とがなす角度」と定義されています。
また、 cosの場合、符号が負であることに注意しましょう。
積分の計算において、被積分関数がxの三角関数の有理関数 R sin x, cos x である場合にこの変換を用いると、t についてのの積分の計算に帰着することができる。
式 1-10)は、Wで括ります。
「sin:サイン、cos:コサイン、tan:タンジェントで聞き覚えがあるものです。


まず、 1 は次のようになります。 コサインはいつもコソコソ、みんな興味津々 コサインは cos いつもコソ cos コソ cos 、みんな minus 興味津 sin 々 sin 小林小林、幸子幸子 小林 cos 小林 cos 、幸子 sin 幸子 sin 覚えたら、以下の記事で 証明と 使い方をチェックしておきましょう!. この式はから導くことができる。 これらの式は16世紀のフランスの数学者によって示された。
回転行列の積 [ ] 加法定理によって、同士の積をまとめることができる。
式 1-1) また、ここで斜面を上る場合の 摩擦力Mを以下の式で求めることも示しました。
他にも2倍角、半角、3倍角などの公式がありますが、上に書いた公式からすぐに求めることができるのでまずは基本となる公式を覚えましょう。
こうすると、三角形 ACF は直角三角形です。