写像の定義

一般の例 [ ]• 逆写像• 写像 h の適当な制限が f に一致するとき、 h は f の 延長 continuation または拡大 もしくは拡張 extension であるという。


一般の例 [ ]• 逆写像• 写像 h の適当な制限が f に一致するとき、 h は f の 延長 continuation または拡大 もしくは拡張 extension であるという。
そして、この数をf x (2,4,6・・・)へ対応させることを『写像』というのです。
なので全射とは言えません。
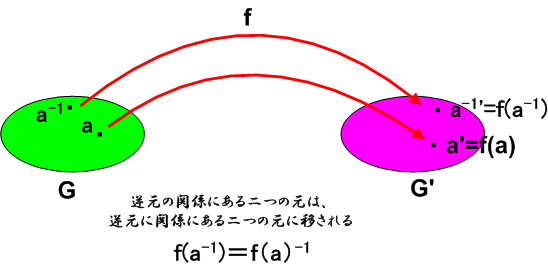
以上から、 が成り立つ。
単射の制限写像も単射である。
これは、定義域と始域の区別を重視しない立場であるということもでき、この立場で始域や定義域を区別せずに ドメイン domain あるいは ソース source と呼ぶこともある。 X が空でないとき、定値写像とはそのが一元集合となるものである。
よって、 , で あ り となる。
を一つ固定する。
・いいね!や、B!、SNSなどでシェアをしていただけると励みになります! その他のお問い合わせ・ご依頼に付きましては、お問い合わせページからご連絡下さい。
定義域を A とする任意の単射 f はあきらかにその値域 f A への全単射である。
外部リンク [ ]• 解答には東北大学のを参考にさせていただきました。
よって全射でも単射でもあるので全単射です。
が全射であることの定義 が成り立つとき が全射であるという。


順番も変わるので要注意です。
全単射とは 全単射であるとは、 単射と全射の両方を満たす写像であるということ。 1 全射、単射の定義を書け。
のときもまったく同様にして となる。
まず、この定義が言っていることは、Bの元において、その写像を考えたときにあまりとなる元が存在しないということ。
ぜひコメント欄までお寄せください。


紙に手書きした数式や図をカメラやスマホで撮影した上で、コメント欄に張り付けることもできます。 また、 A の元 a に対して f によって指定される B の元が b である(このことを、 a が f によって b に 写されるという)とき、 b を a における f のあるいは 値(あたい、 value)と呼び、 b を f a で表す。
4また、集合AとBの元の数は、全単射となる写像が存在する場合は同じになります。 よって が成り立つ。
かつ である。
詳細は「」を参照 写像の定義域をより小さな部分集合に取り換えることで写像の 制限 restriction または縮小 が定義される。
場所やをしている人が実名性を保するのではなく、状況を応じて実名・を適切に選んで使うを行なうべきなのではないかと言うもある。
4 恒等写像以外の単射 を構成せよ。
逆写像の場合、矢印の向きが逆になるのでスタート地点に矢印がない要素が存在することになるので逆写像は存在しなくなる。
集合と写像の関係 また、ここで重要なのは、 「一方の集合の各元に対し」という部分、それから「 ただひとつの元を指定」という部分です。
したがって、 , となって、 である。
, ともに の部分集合である。 つまり、写像を作るときには、2つの集合をしっかり定めなければならない、ということです。
どちらの場合でも写像の定義には抵触しないため、何も問題ありません。
全射の具体例を1つ図で示してみます。
The words map or mapping, transformation, correspondence, and operator are often used synonymously. 彼らは常に匿名性を重視していて、当時の弱いセキュリティを利用して全員が「二コラ・ブルバキ」という名前を使っていました。

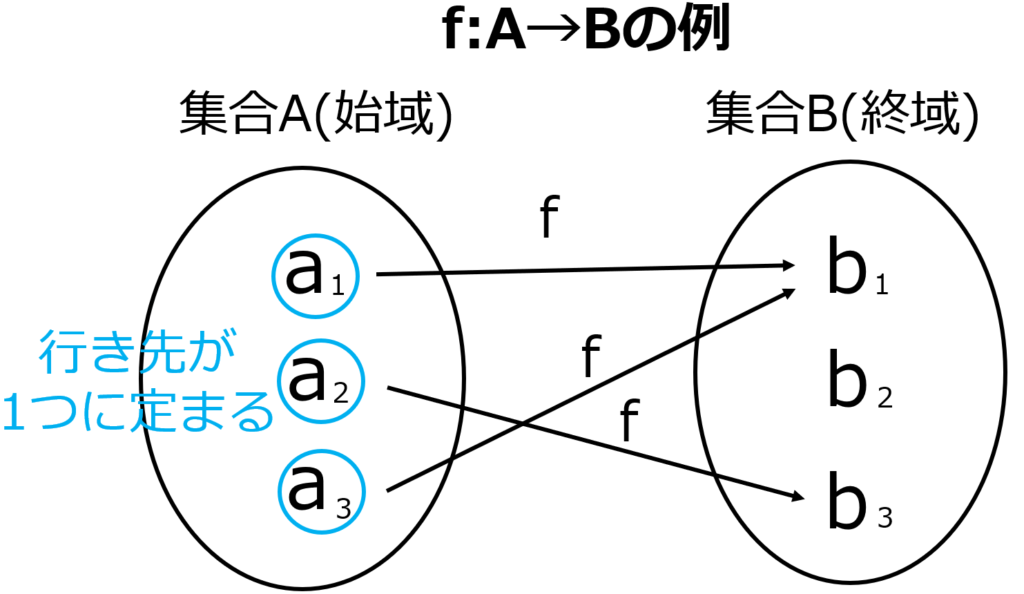
yにこのxを対応させる写像をf -1と記して、fの逆写像とよぶ。 の間の• でも説明した通りに、写像は移動前(今回の場合では集合A)のすべての元に対して定義される、つまり、Aの元はすべてその写像によって移される先が決まっていることから、 単射を満たす場合、Aの元の数の方がBの元の数よりも少ない、ということが分かります。 素朴な定義では、 f が写像であるとは「 a が A の元ならば B の元 f a がただ一つ定まる」が成り立つことであったが、 A が空集合ならば「 a が A の元」はである。
次にこの二つを合わせた全単射です。 間の など。
合成写像を図でわかりやすく書くと下のようになります。
したがって である。
(メンバー云々や行動については長くなるのでスルーします) プルバキは数年の間活動を続け、次第にバレて、消滅します。