三角形の面積を外接円の半径を使って求める

特に、四角形が円に内接する場合は対角の正弦が同じ値になるので公式があります。 高さがhで共通しています。 長方形 最も単純なのは長方形の面積です。
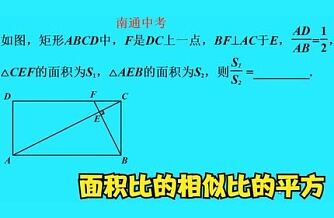
9面積比の算定では、各図形は必ずしも相似である必要は無いです。 代表的な定理をいくつか見ておきましょう。
畢氏定理 [ ]• 各面積の値は下記です。
。
SAS(Side-Angle-Side,邊、角、邊):各三角形的其中兩條邊的長度都對應地相等,且兩條邊夾着的角都對應地相等。
とはいえ…もうちょっとラクにやる方法ってないんですかねぇ? っていう方の願いをかなえるため 3辺の長さしか与えられなかった場合に、簡単に面積を求める特別な公式について次の章でお話していきます。 三角不等式 三角形任意一個外角大於不相鄰的一個內角。
従って3種類すべてを覚えておく必要はなく、どれか一つを覚えておいてその場で作るのが得策です。
六個邊長相同的等邊三角形可以拼成一個。
辺の長さがすべて分かっていれば、角度は必要ありません。

これらは、「 余角・負角・補角の公式(合わせて『還元公式』)」という名前がついているのですが、この公式を覚えることは非常に効率が悪いので(18種類以上もあるのです。 台形の面積公式や三角比の余弦定理をフル活用していきます。 必要なのは2辺とその間の角です。
20<正弦定理の図> 余弦定理とは 余弦定理は、「余弦」と名付けられているようにcosを使った定理です。 今度は平行四辺形ですが、やはり三角比を用いた三角形の面積公式を応用して計算します。
(式3) 2S=ah 式3に式2を代入してhを消去する。
実は三角比を利用することで三角形の面積を求められます。
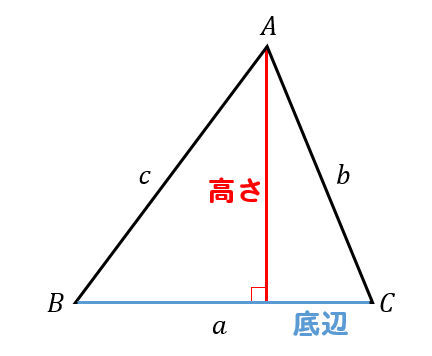
辺BCを底辺と考えた場合 赤線の部分を高さとして考えることができます。
三條的交點 (重心) 三條的交點 被交點劃分的線段比例為1:2(靠近角的一段較長)。 先ほどの面積公式には h (高さ)が含まれているのですが、三角比を用いることで h を用いずに面積を計算します。
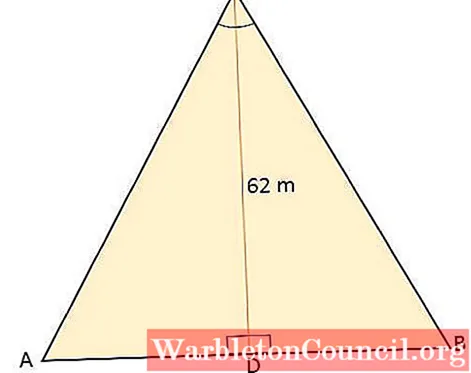
この三角形の面積を求めなさい。
三角形 次に、三角形の面積の計算方法を思い出しましょう。
そして、それぞれの三角形の面積を求めて、合計すればよいと考えていきます。
この記事でご紹介した問題を攻略する最善の方法は、• 似た用語に相似比(そうじひ)があります。 では、次の章では公式を使って計算をするやり方についてみていきましょう。 一般性質 [ ] 三角不等式 [ ]• 面積比(めんせきひ)とは、2つ以上の面積の比率です。
18三角比の表と読み取り方 三角比の値は角によって決まっています。
從右圖可知,將兩個全等三角形相拼,可得一平行四邊形。
これは三角形でも同様です。
このような流れでやっていきましょう。


外接円の半径と面積の公式 内接円の半径と面積の公式を紹介したので、 外接円の半径と面積の公式も紹介しておきます。 ヘロンの公式 2辺とその間の角ではなく、3辺の長さのみがわかっている場合は、余弦定理から角を求めるか、ヘロンの公式を利用して解くことができます。 有人認為退化三角形並不能算是三角形,這是由於它介乎於之間,在一些資料中已否定了其中一條邊等於其餘兩條邊之和的情況。
等邊三角形 [ ] (又稱正三角形),為三邊相等的三角形。 altitude :從三角形一個頂點向它的對邊所作的垂線段。
このように与えられた情報から、どの部分を使えばよいのかを自分で判断する必要があります。
成直角的兩條邊稱為「」(cathetus),直角所對的邊是「」(hypotenuse);或最長的邊稱為「弦」,底部的一邊稱作「勾」(又作「句」),另一邊稱為「股」。
これで三角形の面積がわかります。
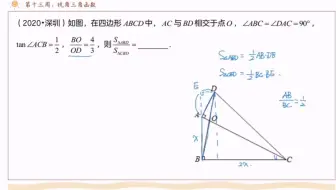
上記より面積比が相似比の2乗になると分かりましたね。 ) その他の三角形の面積の求め方 正弦以外の三角形の面積の求め方についても確認しましょう。 三角比の面積問題でよく利用されます。
1三角形の面積を三角比で表すと…? これまで、長方形や三角形の面積公式を復習しました。
どうしましょう。
これは底辺が同じで高さが異なるとき、面積比は「高さの比」といえます。
(図の赤色の角度です。
やり方を 詳しく説明していきます。 一方、角度は一つも分かっていません。
それは三角形AHCで三角比の定義を使えばいいのです。
全等及相似 [ ] 全等三角形 [ ] 三角形具有穩定性,若二個三角形有以下的邊角關係確定後,它的形狀、大小就不會改變,二個三角形即為。
三角比の相互関係を利用して解くことになります。


三角形の二つの辺と、その間の角度が分かっていれば面積は計算できるという訳ですね。 三角形の面積公式 などの基礎事項の復習から始めること。
12ですので、三つのうちどれか一つを覚えれば十分です。 これも余弦定理の有名な形の一つです。
要は、長さが分かっている2辺の間の角度を使えばよいのです。
なので私たちはこれからこの公式を「三角比が出てくる形」に変えてあげることを考えます。
三角形的面積能從兩角及其夾邊求得。