確率変数と確率分布

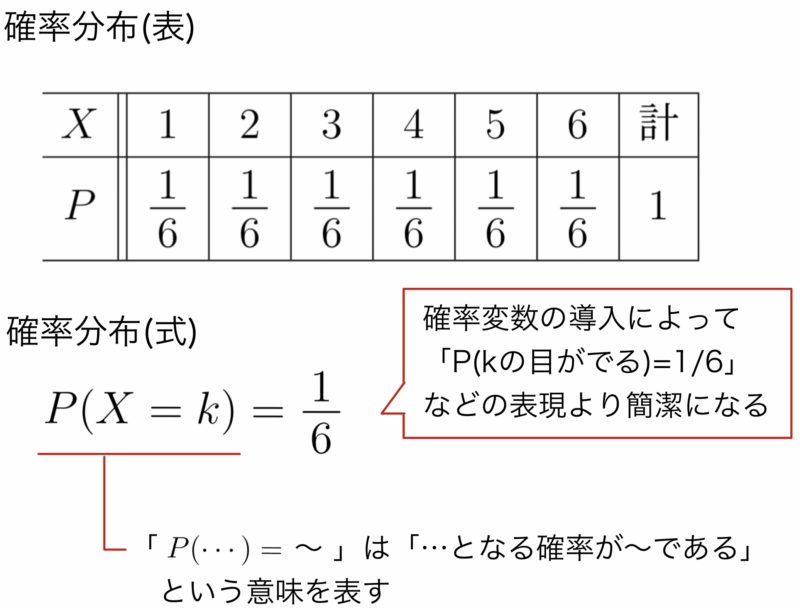
この「確率変数のとる値と、その値をとる確率を対応させた一覧」のことを 確率分布と言います。 離散型確率変数の場合のはで表される。
1前回のコラムはです。
確率分布は X の定義に使われた特定の確率空間を「忘れる」ので、 X の様々な値の確率を記録するのみである。
確率分布が連続でも絶対連続とは限らない。
確率変数は、• 今回は、分布について詳しく紹介したいと思います。
このような確率分布は常にで捉えることができる。
。
どのような値となるかが,ある確率法則によって決まる変数。
ここ、注意してください。
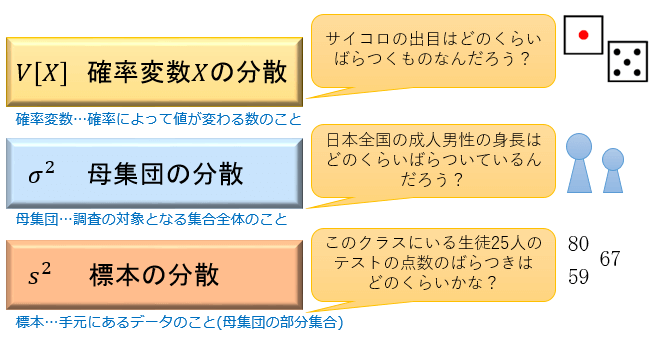
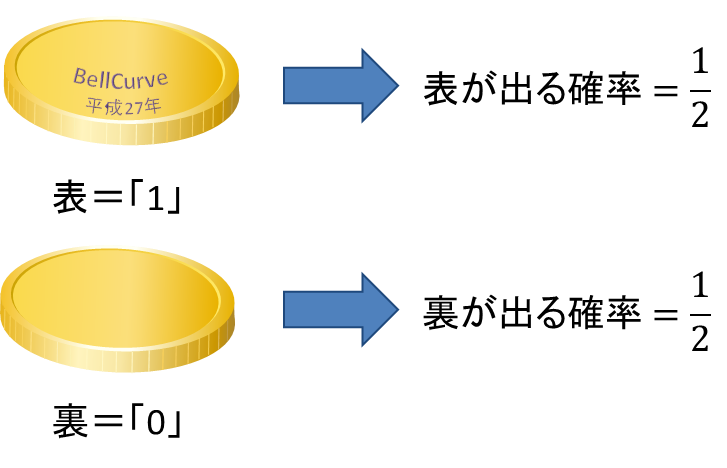
確率変数が関数であるということをより強く意識してもらうためには、次のような図で確率変数をイメージしてもらってもよいです。 そして、面積を図ることができる空間、測度空間上で確率変数を定義しました。 確率変数の同値性 [ ] 確率変数が同値と見なされるには「等しい」「ほとんど確実に等しい」「分布が等しい」といった、いくつかの異なる意味がある。
10標本空間こそが面積を測れる空間のことです。 離散確率変数で表されるデータを計数値 discrete variable ,連続確率変数で表されるデータを計量値 continuous variable という。
標本空間としては「ルーレットの向き全体」を考える。
次回は大数の法則に戻りたいと思います。
2つのサイコロを振るとき、出た目の和の確率分布を調べるには、確率変数を次のように取る。
実数確率変数 [ ] ここでは観測値を実数とする。
これらを表とグラフにすると以下の通りになります。
Hazewinkel, Michiel, ed. 確率変数が可測関数としてならば、が存在する。
いろいろの値をとりうる変数Xがあって、それぞれの値をとる確率が決まっているときXを確率変数という。

Fristedt, Bert; Gray, Lawrence 1996. これらの確率要素は実数値の確率変数(主に乱数ベクトル)として取り扱えることが多い。 しかしアウトカムの標本空間内で2つの確率変数が同時に測定される場合、すなわちある人について身長と子供の数とを同時に調査する場合などは、両変数に相関関係があるのか否かを知るのは容易である。
連続型確率変数の場合の確率はを参照。 『』、1942年。
つまり、その変数が確率変数に代わって確率分布する。
Zukerman, Moshe 2014 PDF , ,• 前回、大数の法則の記事を分かりやすく説明しようという記事を書きました。
概念の拡張 [ ] 統計学における基本として、 確率変数がとる値はであり、従ってやその他の値を計算することができる。
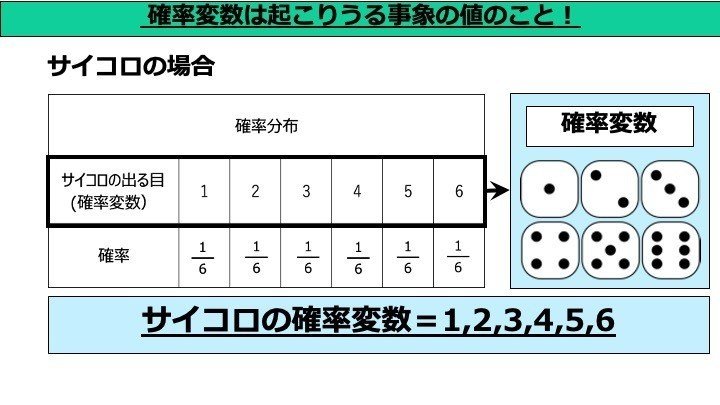
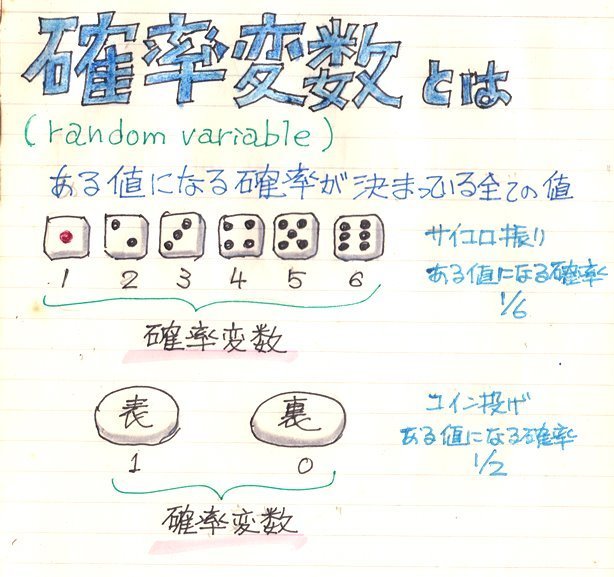
離散確率分布であり、短冊の高さが確率質量を表す。 何方の場合においても、確率値は確率質量関数の要素の和を無限に取っていくことで求めることができる。
6というわけで今回は確率変数の説明でした。
ここで 1 A はである。
そして、確率変数を測度空間(=面積を図ることができる空間)上の関数で定めたため、 ランダムという概念に頼る必要がなくなりました。
連続型確率変数の場合の確率分布は、がならばで表される。