論理回路―記号や真理値表、計算問題の解き方などの基礎知識。
したがって、 4 ビットの加算では、半加算器を 1 つと、全加算器を 3 つ使うことになります。
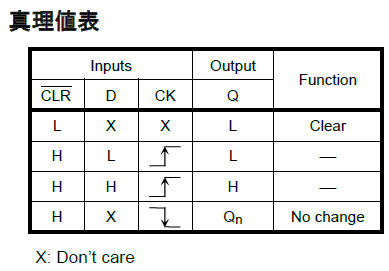
10真理値 真理値とは、命題のうち、正しいと判断できいることを真(True)、誤っていると判断できることを偽(False)、真偽を総称して真理値といいます。
5変数以上の簡略化の場合は、カルノー図ではなく、クワインーマクラスキー法などを使うことが多いです。
コンピュータ内でブール代数や論理演算がどのように利用されているかわかる。
コンピュータは非常に複雑な論理回路であると言うことができる。
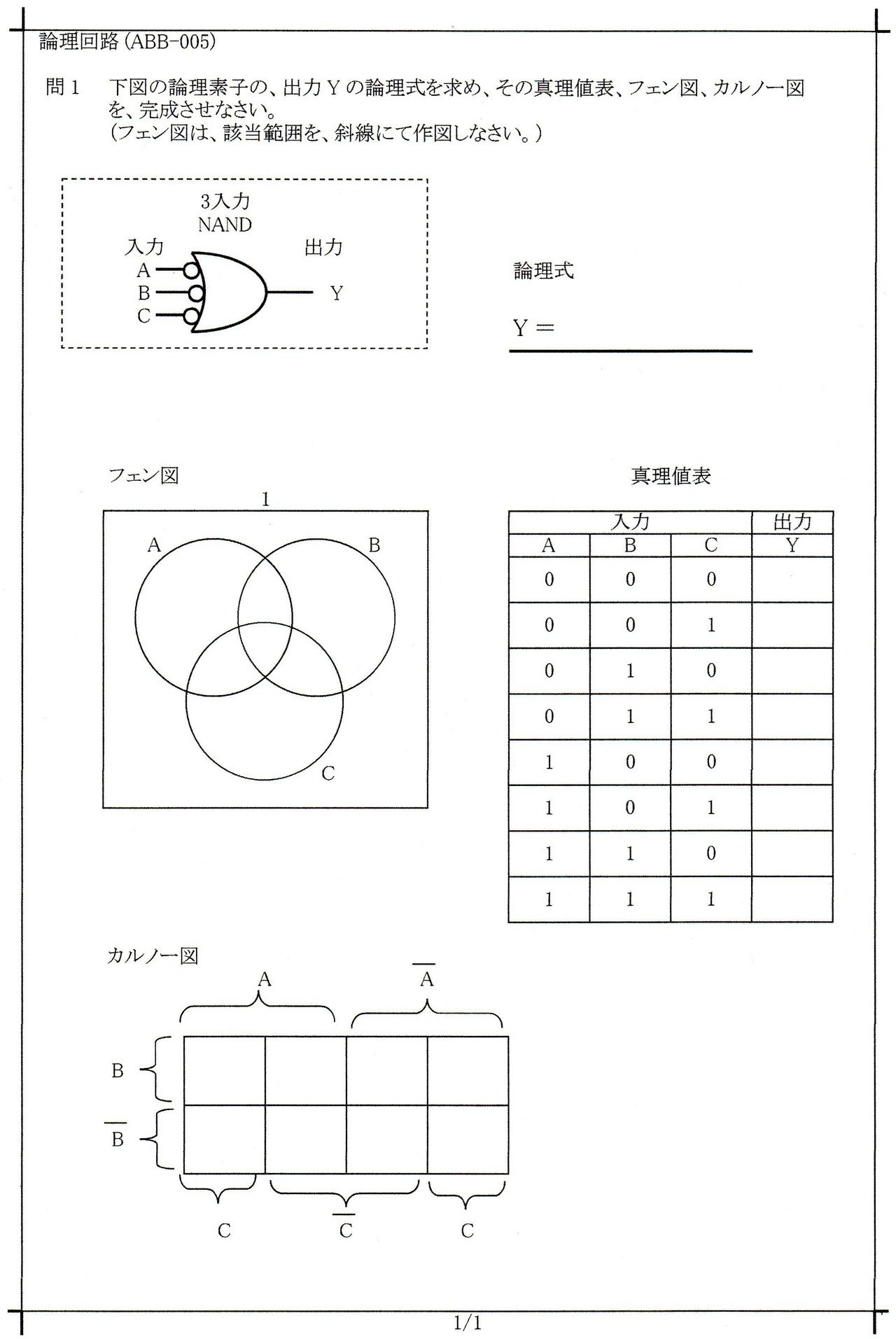
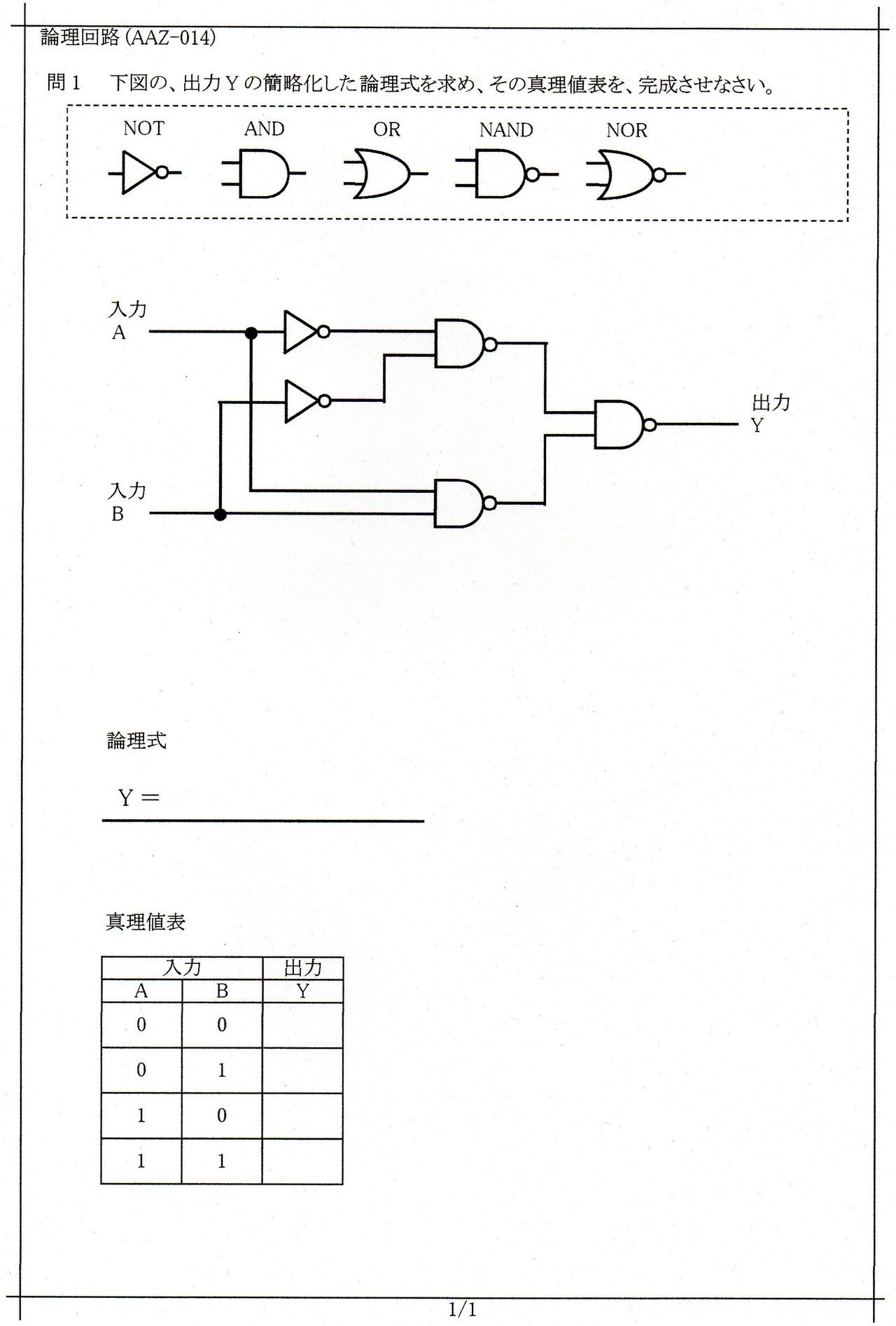
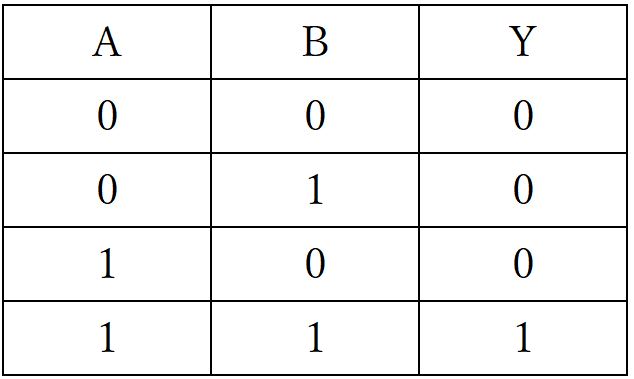
下に一致回路の構成例を図に示した。 真理値表だと00, 01, 10, 11の順番で並んでいるはずですが、00, 01, 11, 10となっていますね。 少し複雑な論理回路で、これを頭の中で計算しようと思っても、途中どこかで間違えてしまいがちですから、地味な解き方ですが、真理値表を作るのが確実でしょう。
5必須主項+Step4で囲った主項の論理和が完成品 最後に、 今まで求めた必須主項とStep4で囲った主項の論理和をとります。
なので、今回の場合は、下のような緑色の囲い方が、論理式を最も単純化する囲い方となります。
囲める組み合わせをすべて調べる(主項を求める) カルノー図では 真理値が1となっている部分にだけ注目します。
カルノー図では、論理式を単純化するためにわざと2ビットのうちの 片方を固定して隣合っている場所が1ビットしか違わないようにするためです。
2つのNOTはNANDゲートで作ることができ、5つのNANDゲートを使う。
情報技術者試験では4つの選択肢があります。
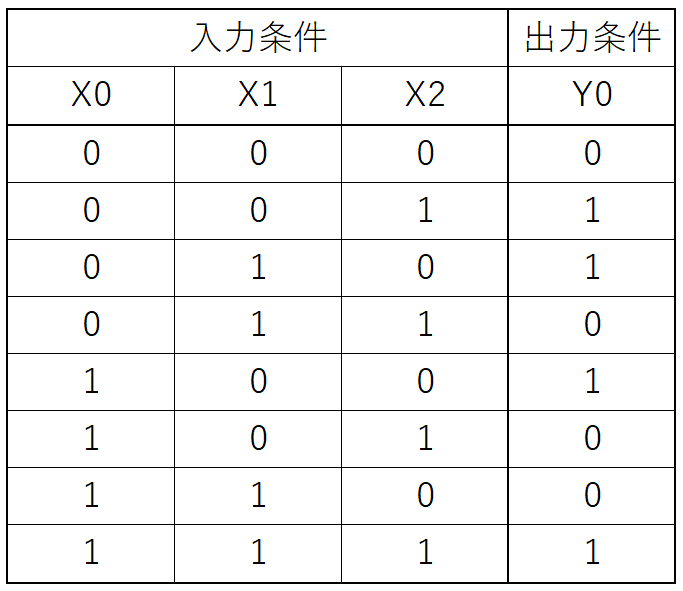
3 変数以上の AND, OR がわかる、真理値表を書ける。
ならばそうした使い方をする場合、 回路図の記号を上図の OR 回路記号のままにしておくよりも、 左のように記して AND 回路的に使っていることを明示した方が分かりやすくなります (入出力の小さい円はを表しています)。

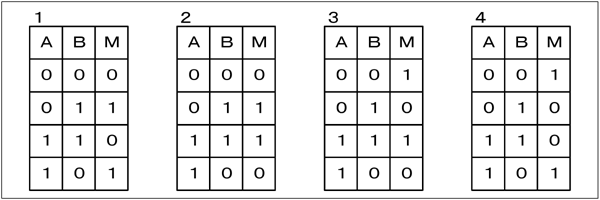
半加算器と全加算器に関する午前問題 半加算器と全加算器の仕組みがわかったところで、午前問題を解いてみましょう。 これらについて、入力の4通りの組合せとP~S、Mの論理を合わせた表が、Fig. 簡単な論理演算、論理関数について真理値表を書くことができる。 グループ化した部分を論理式で表す• 様々な定理の意味が理解できる。
8真理値表からブール式を導き出す方法 先ほどは命題から真理値表を作成しましたが、次は真理値表からブール式を導き出す方法を紹介します。
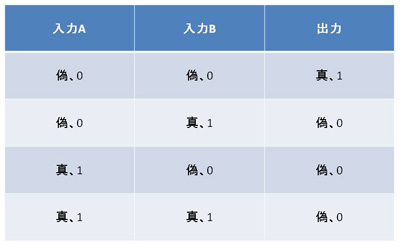
下図の場合入力信号は 2 個なので、 入力信号 A, B の組み合わせは 0, 0、 0, 1、 1, 0、 1, 1 の 4 種類です。
分からなくても差し支えありませんが、 これは論理回路を理解する近道です。
「プログラムはなぜ動くのか」(日経BP)• Step5. 抵抗を付けているのは、A,BがONになった時に大電流が流れるのを防ぐ役割を持っています。
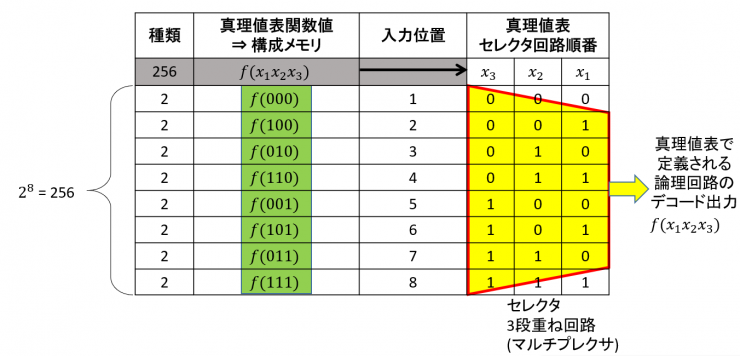
以下では任意に構成された論理関数や論理回路について、• 以下、そんなポイントをまとめてみました。 OR 回路 OR 回路 (OR circuit) OR 回路 (論理和回路) は最も基本的な論理回路のひとつで、 や とともに、 「基本論理回路」 と呼ばれています。
3論理式を求める• 真理値表は以下になります。 確かに上の真理値表の場所と一致していますね。
「これらの結果を見て、論理演算で加算を実現する方法を見出してください」と言われても、すぐにはピンと来ないでしょう。
「出るとこだけ! 独立後、現在はアプリケーションの開発と販売に従事。
まずは真理値表です。
このとき、Aは0、B,C,Dは1となる。 どのスイッチを押しても 「次止まります」 というランプがつきます。 論理式の簡単化 複雑な論理式を簡単化するのにはカルノー図を使用すると便利です。
2その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。 真理値表から論理回路を予測する しかし、どちらのパターンでもやり方は変わりません。
ブール代数が基本 コンピュータでは0と1だけを使った「二進数」を使います。
1が記入されている部分をグループ化• このような個々の項をANDで記述して、それらをORで連結する形を 積和形、 加法形 と呼ぶ。
まずは、複数の入力信号の大小を比較し、その結果を出力する機能を持った回路である「 比較回路 (comparator)」について見てみることにしよう。
図 4 ビットの加算の例 半加算器の仕組み 加算器の仕組みを説明しましょう。 クワイン・マクラスキの方法 公理、定理を用いて論理式を変換する方法は加法標準形を求めるときにも用いたが、論理関数の 簡単化の場合、どこまで変換すれば最も簡単化されたかを判断する基準がないため論理式が複雑に なった場合適切に変換するのは難しい作業となる。
「ifとelseの思考術」(ソフトバンククリエイティブ) など多数. ここでの合成は設計とほぼ同じ意味となる。
やはりAND、OR、NOT3つがあれば複雑なものであっても表現することができるというのが分かります。
論理積 AND• 「 B 」の素子は、桁上がりを求めるので AND 回路です。