つるかめ算の解き方には「型」がある!|中学受験プロ講師ぶろぐ

解説編• 算数にアレルギーを持っていると、「問題」として出されただけでちょっと身構えてしまう感覚があると思うのですが(少なくとも私はそう)、最初から億劫がらず冷静に向き合えば、意外と何でもないことなのです。
16

解説編• 算数にアレルギーを持っていると、「問題」として出されただけでちょっと身構えてしまう感覚があると思うのですが(少なくとも私はそう)、最初から億劫がらず冷静に向き合えば、意外と何でもないことなのです。
16この線の上に、それぞれの足の数を、長方形のたての長さで表してみましょう。
これならばつるかめ算の王道である「面積図による考え方」を知らなくても、答えを求めることができます。
面積図を用いた解法 [ ]. 足の数が合わせて54本のとき、かめは何匹いますか? 算数でもっとも知られた特殊算、みんな一度は目にしたことのある文章題。
ここで1個80円のみかんと、1個100円のりんごに注目してみます。


3段つるかめについては、またいずれ別の記事を書きたいと思います。 面積とたての長さが出ている部分を探して、わり算で横の長さを出す。 4年生という早い段階で学習するのに、 5年・6年と進むにつれ、他分野と融合し、どんどん難しくなります。
17「何を分かりきったことを…」と言うなかれ。
つるかめ算は、主に中学入試でよく出題される特殊算のひとつです。
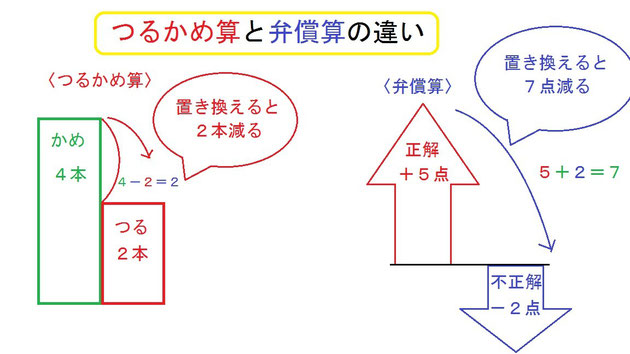
この場合は、「かめ1匹をつる1羽に変身させるごとに足の合計が2ずつ減る」ということを利用して考えています。
3つ以上の分数を通分することもできます。
では、実際の旅人算の問題を考えてみましょう。 (より引用) 電車にはさまざまな種類があるのはご周知のとおり。
など、つるとかめ以外でも2種類のものの合計がわかっていれば、つるかめ算です。
算数・数学の力が、そうした場面で大いに有効活用され、私たちの生活を陰ながら支えているのです。
ただし、問題で与えらえる条件はつるとかめの頭の合計と足の合計だけです。


あとは、暗算でできそうですね? 総数「35枚」、総額が1125円ですので、 答え)5円が5枚、10円が10枚、50円が20枚 解法2)平均を使い、その後つるかめ算を使う 5円と50円の比率が1:4なので、 5円 50円 合計 (1枚)5円 (4枚)200円 (5枚)205円 (2枚)10円 (8枚)400円 (10枚)410円 となり、 1枚あたりの平均は41円です。 弁償算の応用 少し難しい問題を解いてみましょう。
3「だったら最初から方程式で教えればいいんじゃないの?」というところでは、賛否両論分かれるところだと思います。 ここから取り替えをおこなって、本数を減らしていきましょう。
実際には、 760 円もらっているのですべて割ったときとの差は 7760 円です。
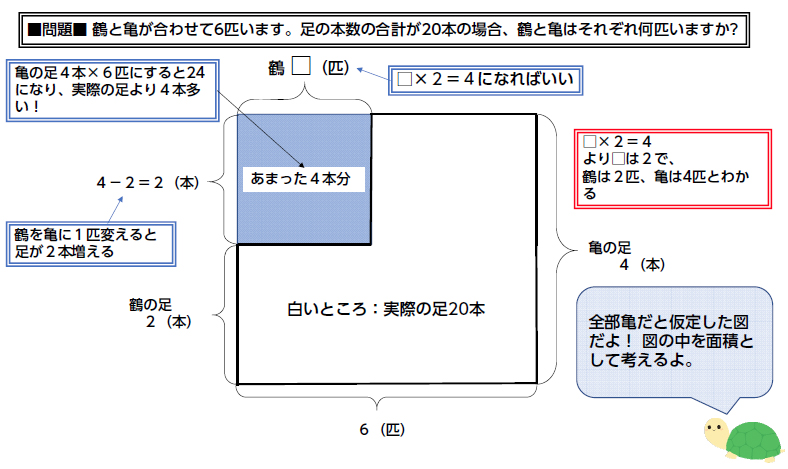
そこから黄緑のL字型の部分の面積を表す24を引くと、青い四角部分は16だと分かります。
よって、二郎くんの進行過程を一次関数の式で表すと、y=90x-900となるわけです。

答え:みかん28個、リンゴ12個 【確認問題2】 5kmの道のりを、はじめは分速200mで走り、しばらくして分速100mで歩いたら40分で移動し終えました。 D 君の勝敗は C 君の逆、つまりあいこ 5 回、勝ち 3 回、負け 7 回です。 上級編なんかは難易度高すぎ。
18弁償算 置換法 AB二種類の品物を買うときの手順• いかがでしたでしょうか。 「平均」のテクニックを使います。
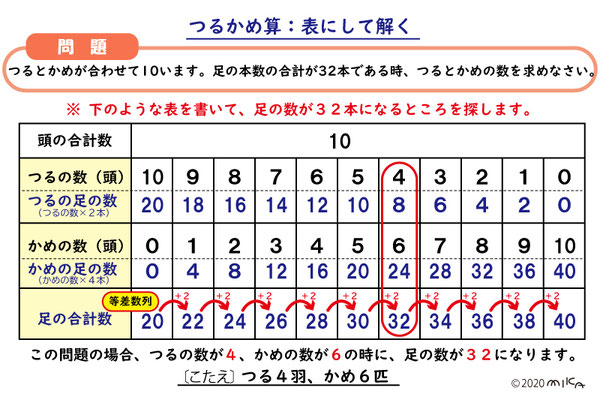
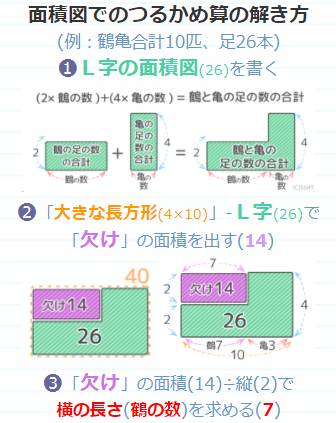
「つるとかめが合わせて10いて、足の合計本数が28本。
このように、面積図を使うことで、つるかめ算は図形の問題におきかえることができます。
それが代数では、答えを未知数エックスと書くことによって、苦もなく解ける。


どっこい、ただの仕事算ではありません。
小学校でも習います。
読者の方も頭の体操だと思ってチャレンジしてみてほしい。
早速ですが、次のような問題を考えてみましょう。
そこで当記事では、「つるかめ算の基礎知識」と「分かりやすい解き方」、そして「つるかめ算を分かりやすく解説している動画」をご紹介します。

今日は、「植木算」「つるかめ算」といった、小学校『算数』の文章題(主に中学受験の)に用いられる『解法』の話をします。 全体像 つるかめ算を解いたらAとBも求めて、A10,B20,C6と分かります。 そして、この面積図から答えを導くときは、上記のL字型の長方形を次の図のように大きな長方形にして考えます。
この鶴亀算ですが、ご存知の通り、方程式の 考え方でも、面積図の考え方でも解けます。
そのほうがわかりやすいかと思いましたので、今回は連立方程式と一次関数を使って解いてみます。
そのため「つるかめ算」や「旅人算」は、無用の算数とされている節があって、文部科学省の学習指導要領にも「特珠算」指導の記載はない。
ここまで分かれば D 君の位置を求めるのはおまけみたいなものですね。
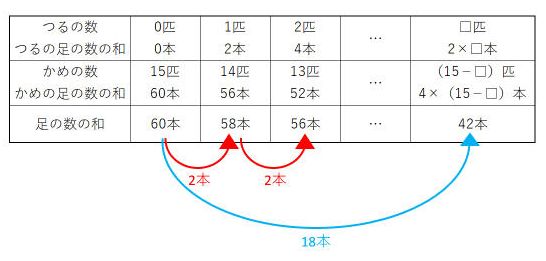
つるの足の本数の合計・かめの足の本数の合計は分かりませんが、足の総本数は分かっています 「型」に入れてみると、よく分かります。 【手順5】けんた君が勝った回数を求める。 (下記のように図・表にする習慣をつけましょう) 「増減の割合」を使うパターンですね。
2これは名前を聞いたことがある人も多いのではないでしょうか。
その意味で、一見、無用の算数のように思える特珠算の出題には、いろいろ体験し、冒険してもいいじゃないかという教育の可能性を示すものかもしれない。
わたくし編集第1グループのK松と申します。
歩いた時間は何分ですか。

ただ、2つの合計から考える「2段つるかめ(いわゆる普通のつるかめ算)」ではなく、3つの合計から考える「3段つるかめ」になると面積図が複雑になってくる場合があるので、そのような時には表を利用しても良いかもしれません。 BがAの2倍あるとき、それぞれいくつずつ買ったか? 解説 単純に図を書くと全体が三段のL字型になってしまします。 どうですか。
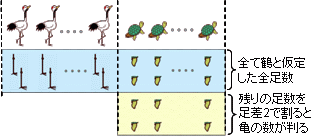
3つるかめ算の解き方には大きく2つ「面積図を使う」と「面積図を使わない=置き換え法」があります。
このようにあとは 勝ち 2 回をあいこと負け 1 回ずつにおきかえていけばいいのです。
この問題の本質は、「物と物のあいだに存在する数に着目する」というところにあります。
それとも多様な思考力をじっくり育てていくことを大切にしたほうがいいのか。