バリニオンの定理|受かる構造力学

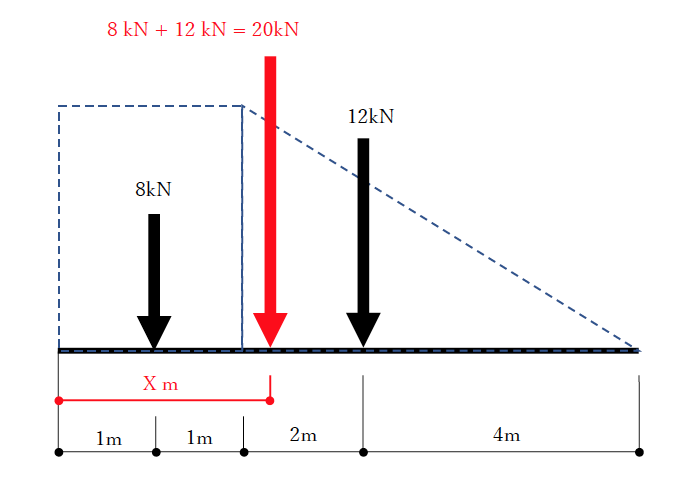
つまり分力の作用線上に点Oを決めます。
2白ワイン産地、 リアス・バイシャスから 「ビオンタ」の生産地はスペイン北西部ガリシア州。
. 数学の分野では やの研究で知られ、の分野ではオランダの が記述したの概念を進め、1688年に、力の平行四辺形によるの概念を明確にした。
Fermat-Torricelliの問題に対する未知の解決策. デュムランはステージ優勝したに続くステージ2位でフィニッシュし、キンタナとニバリはデュムランに押し出される形でそれぞれ1つずつ順位を下げた。
つまり用語を使用する分野自体が異なるのではないかと思います。
次に 合力が点Oを回す力を考えます。
これを機械的(図式的)に行う方法として示力図・連力図という方法がありますが、ここでは述べません。
質問一覧• Varignonの平行四辺形が形成されていることを確認します. まとめ バリニオンの定理は地味ですが、別記事に書く等分布荷重の合力を求めたり、剛体に働く平行な力の合成の作用位置を求める算式解法としても利用できます。
2度目のジロ総合優勝 [ ] 2016年、では序盤〜中盤にかけて不調に喘いでいたが、チマ・コッピを越える頂上ゴールの第19ステージにおいて、当初総合で2位以下に3分以上の差をつけて独走していたが落車し肋骨を骨折。

EFGHの和集合が平行四辺形かどうかを判定. 中立丸軸や角形などの単純な形状において,中立軸は断面図形の 図心(centroid of area)を通過する。
17000・・・1mmでも偏心していれば力に対する距離が発生し成り立つのに 合力0のこの一箇所だけには分力のMの和との法則性が途絶えてしまう。 下の図を見てください。
なお、商品・発送等に関するお問い合わせは当ショップまでお願いいたします。
断面二次モーメントとは 曲げモーメントに対するはりの部材の変形のしにくさを表した量である。
式で表すとこうなります。


数学の分野ではヴァリニョンの定理や対数螺線の研究で知られ、静力学の分野でのピカルの定理(力の平行四辺形、力のモーメントの和に関する)などでも知られる。 曲げ応力は,「変形前に平面であった断面は変形後も軸線に垂直な平面を保つ」という ベルヌーイ・ナビエ(Bernoulli-Navier)の仮定を基にして求めることができる。 つまり、これらが平行かどうかを知ることができ、四辺形のセグメントを次のように関連付けます。
19菱形と四角形の領域を決定する. これを解いていきます。 いかがだったでしょうか? 平行な力の合成も分解もバリニオンの定理が重要になります。
合力Rの分力は Paは4N 上向き Pbは8N 上向き となります。
この本の出版は彼の死後何年も経った。
さて、どうだったでしょうか? 「いや、算式解法ムズイ!」ってなりましたでしょうか? そうだとしたら解説の仕方が悪かったです。
また,垂直応力度の合力が軸方向力である。
よくわからないようでしたら、先生や教授に説明してもらうのが一番いいと思います。
また、四辺形の対角線の長さが同じで、垂直でもある場合、平行四辺形は正方形になります。
バリニオンの定理より 点Oを分力が回す力と、合力が回す力が等しくなります。
さらに「ビオンタ」はリアス・バイシャスの5つの小地区の中でも海に面したバル・ド・サルネス地区にあり、海岸までは直線距離でわずか2. 個人タイムトライアル3位 2004年 [ ]• ここでは 分力と 合力が書いてあります。
ウェブ(web) フランジで挟まれる板をウェブと呼ぶ。
図心の定義より,次式が成り立つ。
xが何の値だったでしょうか? xはPaの大きさでした。

総合3位(第16ステージ優勝)• -6y N・m それぞれを足してあげます。 「やじろべぇ」が釣り合っているのと同じ原理です。
上式は図心を通る直交軸に関する断面一次モーメントは 0 となることを表している。 資格・免許 デジタルコンテンツのため記載事項はありません。
一方、四辺形の対角線が垂直の場合、平行四辺形は長方形になります。
示力図の説明は「」 連力図の説明は「」 にて説明していますのでそちらでご確認ください。
つまり、合成不可能な特殊なパターンです。
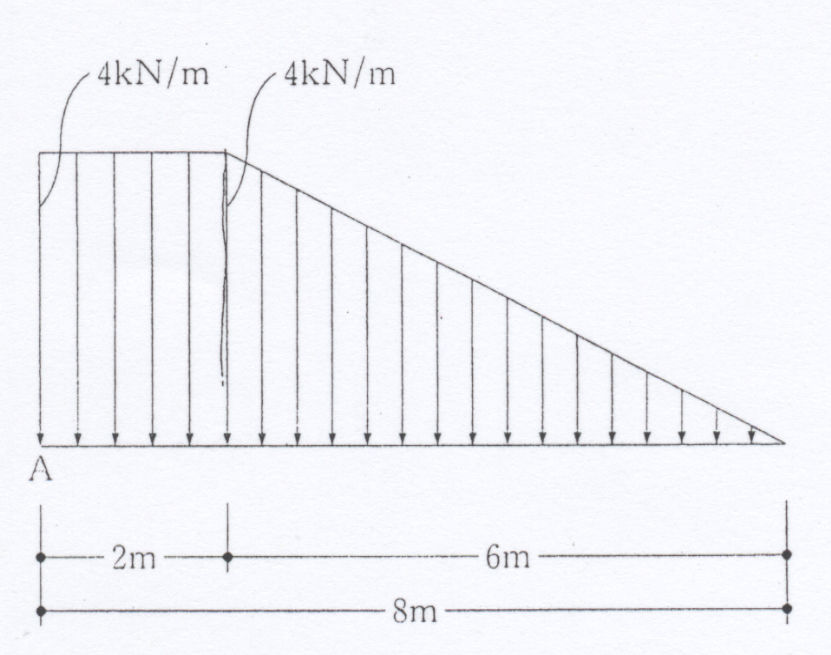
四辺形の辺を比例するセグメントに分割するために. ここでより重要なのがバリニオンの定理です。 平行な力の分解…一見簡単そうに思えるでしょうか? これが意外と難しいです。 長方形管は,中空長方形,角パイプともいう。
12気を付けてください。
では、早速下の例題から考えていきましょう。
一方,はりの軸線方向には荷重が作用しない場合を考えるから,断面に垂直な応力の軸方向の合力は 0 になる。
合力Rの大きさは1000N 下向き でP1の作用線上のO点から右に4mの位置 早足ながら今回も少し丁寧にまとめてみました。