線形 代数 と は。 線形代数が意味不明だったから何に使われるのか調べてみた

線形代数が意味不明だったから何に使われるのか調べてみた

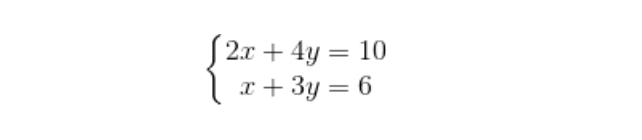
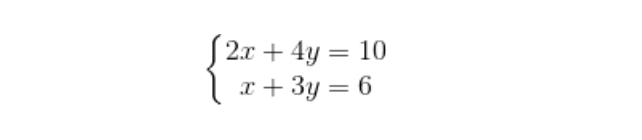
「微分・積分」は「解析学」に属す概念でありながら、フーリエ変換やラプラス変換は線形代数における基底の変換になっている、と理解することがポイントです。 線型変換の構成に関する研究全体で、ケイリーは行列の積と逆行列の概念定義した。

5

そのため、線形代数は漠然とただ学ぶのではなく、自分が将来携わりたい分野にどう活用されているかをしっかりと理解して勉強することが学習へのモチベーションを維持するためにとても重要になります。 というのも、行列は、 連立方程式を簡単に書くために生み出された経緯を持つのです。

• つまり、一様な温度ということです。

• そして行列、ベクトルが重要だとわかりました。

• が、だからなに？連立一次方程式が解けると何かいいことがあるの？という感じです。

大学数学で学ぶ「線形代数」とは

量子力学を学ぶときにも再び利用されます。 同様に土木や建築、機械などの構造設計では、コンピューターを使た数値計算や、エンジンの振動解析や流体解析に線形代数の知識は必須だとか、検索エンジンのアルゴリズムは固有値と固有ベクトルで作られてるとか。 方程式じゃないじゃん、違うじゃんと思いましたが、 そもそも行列自体が、連立一次方程式を簡単に書くために生み出されたという経緯があります。

17

そして、 勉強する際は暗記してはいけません！ 理解する事が重要です。

• 。

• 。

• 公理的な（実数体上の）線型空間の定義や線型変換の定義はによってに与えられ 、までには有限次元ベクトル空間の理論が現れた。

「簡単、ざっくり解説」線形代数のイメージを掴もう!!

その時には「」か「」で質問してみましょう。

10

なので、言い回しが柔らかい二冊目も購入しました。 私が機械学習の勉強時に調査したことをまとめていきます。

• そもそも重要とか必要とかいうレベルではなく、誤解を恐れずにいえば「 線形代数は理工系の学問のほぼ全ての領域にわたって必須」と言ってよい学問です。

• こちらの本のオススメポイントは以下の点です。

• 今まで扱ってきた「2」「5」みたいな単体の数字（ スカラーと言います）とは違った世界をお楽しみいただけるかと思います。

線型代数学

linalg. 関連項目 [ ]. 線形代数自体の参考書としては、 線形代数（行列とその標準形），伊理正夫，韓太舜，教育出版． をあげます。

2

ベクトルもまた数字の並びですので、行列の一種として扱われます。

• 個人的に難しめの本を読むときは、演習問題はやらない事にしています。

• それよりは、「Linear Algebra and Matrix Theory」 Academic Press ,「Linear Algebra」 Springer ,「Linear Algebra done right」 Springer といった本を読んだ方がよいと思います。

• 簡単のため、熱伝導率を1としています。

線形代数とは

今日は、理系大学生やデータサイエンティストにとって切っても切れない縁がある線形代数の勉強法について解説したいと思います。 。

13

理 […]. 20世紀初頭…多くのアイデアとこれまでに登場した抽象数学の概念が導入され現代の線形代数学になっていく。

• 各平面の交わる領域が1点となる場合のみ解が一意に定まり、交わる領域が線の場合に解は無数に存在し、交わる領域が無い場合 例:全ての平面が平行である場合 には解は存在しない。

• ん？ 確かに行列を使って連立を解く、ということを大学の授業でもやったけど、それは全体のほんの一部しかなかったぞ。

• ステップ３までが完璧に出来たらこちらの本に取り組んで理解を深めると、線形代数を応用出来る様になります。

大学数学で学ぶ「線形代数」とは

そういった時のために、必要だからやるのではなくて、どうして必要なのかを明言できるとモチベーションは違ってくると思います。 何に役立つの？ 理工系の学生は、大学に入っていきなり線形代数なんて聞いたこともない学問を習わされる羽目になるわけですが、これには理由があって、ズバリ数学の中でも応用が効く分野で、世の中でバンバン役に立っているからなんですよね。 複雑な計算式に数学独自の思考回路、とにかく難しいイメージのある大学数学。

12

以下で実線形空間で述べることは、複素線形空間でもそのまま成り立つ。 線形代数の概念が分かりやすく図解されているページが多い• ただ、理論的な言い回しで、一から始めるには少しとっつきにくいと感じるところもあります。

• 以下では、微分方程式を離散化すると、線形代数が顔を出す様子を見てみましょう。

• 歴史的には行列式は行列より以前に現れている。

• こういった線形代数や自分が知らない分野の勉強をするときは、難しくて思うように進まない時が多々あります。

線形代数って何？

そして、実際にCG・グラフィックスのプログラミングの勉強をする時は「ゲーム制作者になるための3Dグラフィックス技術」（インプレス）が網羅的です。

14

、は著書「Theory of Extension 拡大の理論 」を出版し、この本には今日の線型代数学の基本概念に相当する 当時としては 新しい内容が含まれていた。 なぜ、学んでおいたほうがいいのかという目的、概要をまとめたものです 線形代数の勉強を始める際は、初学者が自分にあったものを選ぶのは難しいので、書店で手に取って見たり、amazonのレビューをよく読んで選ばれることをオススメします。

• 「大学で線形代数を勉強しなかったよ・・・」と言う人もご安心下さい！ 大学の授業よりずっと分かりやすい教材が多く出回っています。

• 線型代数の重要性は、他分野で必須事項として用いられることにあります。

• 微積分の意味，森毅，日本評論社． 線形代数なのに何故微積分？と思われるかもしれませんが、この本には線形代数の本質的な重要さが紹介されています。