シュミットの正規直交化についてわかりやすく解説してみる
bcc金属のすべり系 bcc金属のすべり系はfccに比べてやや複雑である。 その ため、カーテシアン座標系と曲線座標系を比較して、必要な諸量を計算する。
8bcc金属のすべり系 bcc金属のすべり系はfccに比べてやや複雑である。 その ため、カーテシアン座標系と曲線座標系を比較して、必要な諸量を計算する。
8最後にひとつ注意を与えておく。 「すべりが生じる」ということと「すべり系が働く」というのは同じことです。
これまではカーテシアン座標 と他の直交座標 系 を分けて話した。
行に関する余因子展開を第1行から第n行まで書くと、 となる。
なるほど、、! ではどうして正規直交化をわざわざする必要があるのでしょうか? 次のベクトルたちを見てください。
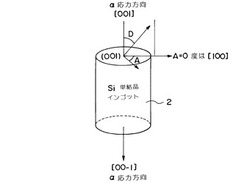
シュミットの正規直交化を使えば長さが1で直行するベクトルたちを作り出すことができるのでとても分かりやすい形で他のベクトルを表すことが可能。 たとえば、ある任意 の点は、極座標の で表現しても、カーテシアン座標で表現しても、一 意に表すことができる。 これが曲線座標系を使う場合の面倒くさい部分である が、しょうがない。
9曲線座標系での位置は、 で表せるが、それはそこで使う単位ベ クトルの成分とならないのである。
曲線座標系と言っても、おなじみの円筒座標系や極座 標系のことである。
定義と定理8.15から 基底は、無数に存在する。
以下、それを紹介する。
上の表に示したように、各すべり系の数は6、12、24個である。
手順 1.a 1=x 1 とおき、e 1=a 1/ a 1 とする。
式 の示すところをみると、スケール因子の2乗の計算は 簡単である。
スケール因子と言う名前はその働きを、よく表している。
金属学では結構有名な問題ですね。
。
もっとよくスケール因子のイメージが湧くのは、座標を のみ変化させた場合である。
定理 余因子を使って|A|は (i:固定) と書ける。


は一般化座標とでも言うもので、スケール因子を乗じることにより長さの次元のおなじみの座標になる。 それにも関わらず、接ベクトルではなくスケール 因子を使のは、• カーテシアン座標系と極座標系 曲線座標系 の単位ベクトルを図と に示す。 社会に大きな変化を起こし、未来を創るために活動し続けるのは容易なことではありません。
12この集合をW 1のW 2の 和空間という。
そして、それらには1対1の関係がある。
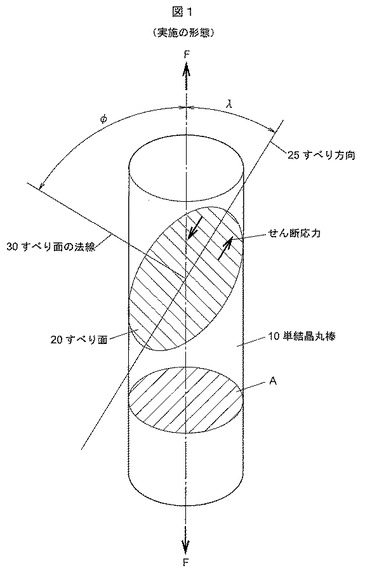
多重すべりの意味を調べてみると、主すべり系と二次すべり系 主すべり系以外のすべり系 が同時に働くすべりとのことですが、よくわか. すべり変形は、すべり面に沿ってせん断変位が発生することで生じるため、外力をせん断応力に分解することからはじめる。
さらに、それぞれの曲面、 、 、 曲面はそれぞれ直交しているので、単位ベクトル同士も直交している。


また、絶対位置のスケールでないことに注意しておく。 それを導くために、式 の両辺を2乗し、式 を代入す ると が得られる。
[ Previous: ] [ Up: ] [ Next: ]• いいかえると、線の上ならば二つ、線の交点ならば4つのすべり系が働きます。 この式を、 第 i 行に関する余因子展開という。
したがって、ここで述べている曲 線座標系 のお互いの軸は、直交することになる。
これは、スケール因子を決めている式 を考えればよい。
これを、 第 j 列に関する余因子展開という。
これ以降、この面倒な部分の取り扱いを延々と示すことになる。
後で述べるが、カーテシアン座標系のスケール因子 は1である。
問8.18 p177 問題(1) p178 問題(2)• 他の単位ベクトル、 や も同じよ うに説明できる。
ただ、この取り扱いが少し難しくなる不利益よりも、多大な利益を得 ることができることがあるため、曲線座標が使われることが多い。
この位置ベクトル の取り扱いについて、ここでは述べる。 問8.19. それは、線素や面積素、体積素がすぐにわかることである。
これを補うために双晶変形が大きな役割を果たす場合も多い。
(どの列で展開しても、その値は等しい。
従って、 は正の値となる。