中学2年生数学

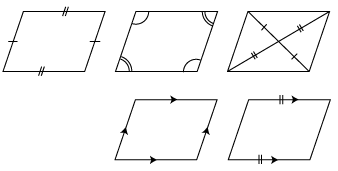
問題の見方 平行四辺形という条件をもとに,辺の長さや角度を求める問題です。
14いえるものは、平行四辺形になるための条件を答えなさい。 平行四辺形とは? 定義 まずは、平行四辺形と呼ばれる図形とはどのようなものなのかを説明していきます。
ポイント ただし,「2組の対辺が平行=平行四辺形」と覚えるだけでは,平行四辺形の証明問題は解けません。
私の考えた結果は、 1 この条件では平行四辺形になりました。
次の四角形ABCDは平行四辺形であるといえますか。
2 この条件では平行四辺形になりませんでした。 ぜんぶの辺が等しい四角形。 3 (4)では平行四辺形にホントになるのですか? なる場合はどのような条件になるのですか? また、平行四辺形にならない図はかいてあるような図でいいのですか?• これから紹介する成立条件の中で どれか1つでも当てはまっている四角形は平行四辺形になります。
12なぜこれでひし形の面積が求められるのかはこちらに解説しています。 。
ひし形:すべての辺の長さが等しい四角形• たとえるなら、 ひし形と平行四辺形の関係は「寿司」と「マグロ握り」の関係に似ている。
平行四辺形の性質を利用する問題 問題1 図の平行四辺形ABCDで,x,yの値を求めなさい。
冒頭でもいいましたが、証明は覚えなくても良いですが、性質は必ず覚えるようにしましょう! 参考 平行四辺形の上の3つ以外の性質として、 「平行四辺形は点対称な図形」というものがあります。

[1][4]、[1][9]、[1][11]、[2][3]、[2][10]、[2][12]、[3][5]、[3][6]、[3][7]、[3][8]、[3][10]、[3][12]、[4][5]、[4][6]、[4][7]、[4][8]、[4][9]、[4][11]、[5][7]、[6][8]、[10][12] は平行四辺形と同値でなく、それ以外は同値という結論になりました。 だから、マグロ握りというのは「寿司」というグループの一種にすぎないわけだ。
12このことから ひし形は平行四辺形でもあるということになりますね。 図としては平行四辺形もできますが、台形もできるのでだめだと思います。
関連記事 「平行四辺形の証明」について詳しく知りたい方は 「平行四辺形,長方形,ひし形,正方形の違い」について詳しく知りたい方は 3. 平行四辺形という大きなグループの中で、すべての辺が等しくなっているものをひし形というんですね。
まずはこの定義をしっかり覚えておきましょう。
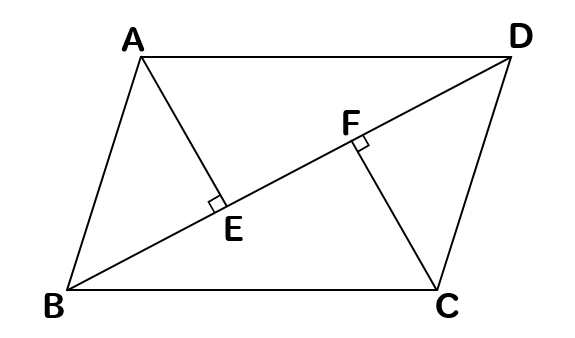
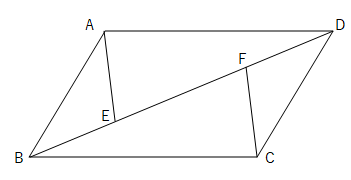
平行四辺形ABCDを対角線BDで折り返し、Aに対応する点をEとし、BCとDEの交点をFとする。


平行四辺形の成立条件その2:2組の対辺がそれぞれ等しい かなり簡単に証明をします。
平行四辺形の定義と条件、必要条件、十分条件 平行四辺形の定義=二組の対辺のがそれぞれ平行な四角形 ーーQ 平行四辺形であるための条件は以下の一つを満たすことである ーーP 1、二組の対辺がそれぞれ平行である 2、二組の対辺がそれぞれ等しい 3、二組の対角がそれぞれ等しい。 ココが大事! 平行四辺形であるための条件 覚えることがたくさんあって大変ですよね。
平行四辺形を面積を変えずに長方形の形にするという方法です。
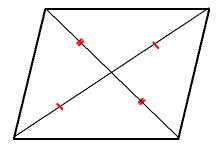
平行四辺形の性質その3:対角線が他の対角線の中点を通る 少しわかりにくいと思いますので、もう少し詳しく説明します。
つまり、 ひし形は平行四辺形である といえるんだ。
条件:2組の対角がそれぞれ等しい が当てはまると思います。 図にまとめたので確認してみてください。
この記事は、 「平行四辺形の証明問題がわからない…」という人に向けて解説 します。
正方形:すべての角が直角ですべての辺の長さが等しい四角形• 2組の対辺がそれぞれ等しい。
条件はどのようになるのかわかりませんでした。
平行四辺形の成立条件 最後に 平行四辺形の成立条件について説明します。
三角形の合同条件と同じように,証明問題ではこの文言が必要となります。
長方形:対角線が 互いの中点で交わる& 長さが等しい• つまり、 いろいろな平行四辺形の中の1種類として、 ひし形 があるってことさ。
2組の対辺がそれぞれ平行である。