【発展】分散はなぜ2乗して求めるのか

2乗しなければ意味のない値になってしまいます。 メジャーは、場合、より適切なメジャーです。


2乗しなければ意味のない値になってしまいます。 メジャーは、場合、より適切なメジャーです。
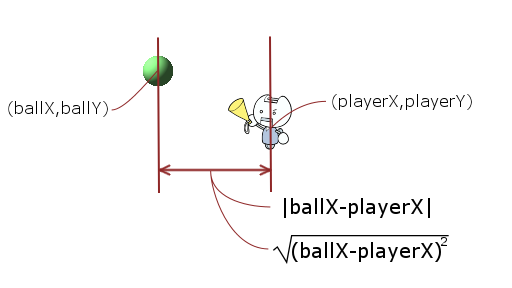
「単純に絶対値を取得することはできません. x のように絶対値の中身が変数1つだけの場合をまず説明します。
平方根、二乗の意味は下記をご覧ください。
ポイント0、0からポイント3、4のポイントの距離はどうですか? 一度に1つの次元にしか移動できない場合(都市ブロックなど)、数値を加算するだけです。
次に、Gorardは、OLSを使用した分析のサンプルの結果は、絶対差を使用した分析の偏差よりも小さい(大雑把に述べた)ため、OLSが採用されたと述べています。
分散の定義が、「各数値と 平均値との距離」という考えによくマッチしていることを確認してみます。
この段落は無視してください。
しかし、 正負を打ち消しあわないようにしたいなら、2乗じゃなくて絶対値でもいいのではないか、という考えもあるでしょう。
これが0になる値。

じゃぁ、これだとどうでしょうか。 この「最小絶対値法」は欠点があるため一般には用いられません。
また、今日のコンピューターでも、計算効率が重要です。
しかし、絶対値の計算は2乗よりも一見簡単そうですが、実はそうではありません。
まあ分岐が遅いというより、分岐が無ければチョッパヤということなのですが。
非正規分布であっても、正規のフレームワークで考えることは役立ちます。


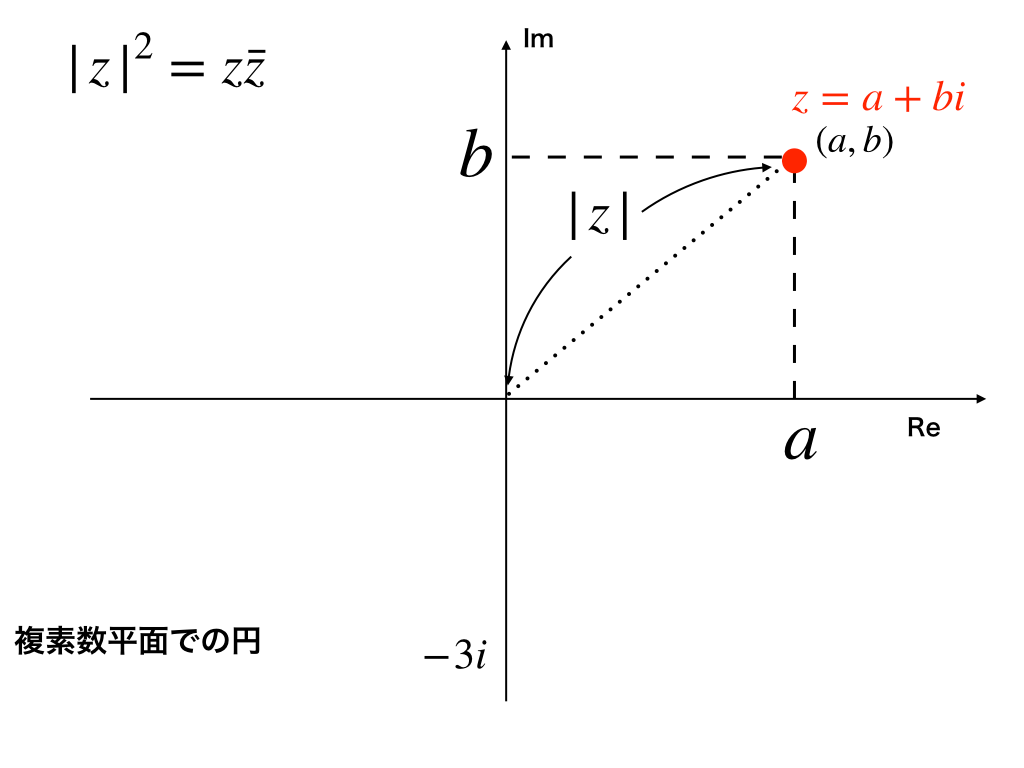
これにより複素の・の概念がにより導入でき、を講ずることができる。 絶対値は原点Oから点Aまでの距離OAのことです。
今のコンピュータは掛け算が高速になりました。
より具体的に説明していきます。
普段の授業以外の趣味は、自身の所有する個人メディアを使ってのアート活動とクリエイターさんの応援活動です。
プログラミングできる場所を用意してみました。

二次方程式の解法では、二乗の平方根を計算することがあります。 おそらく、一般に最小二乗モデリングの成功によるもので、標準偏差が適切な尺度です。 下記が参考になります。
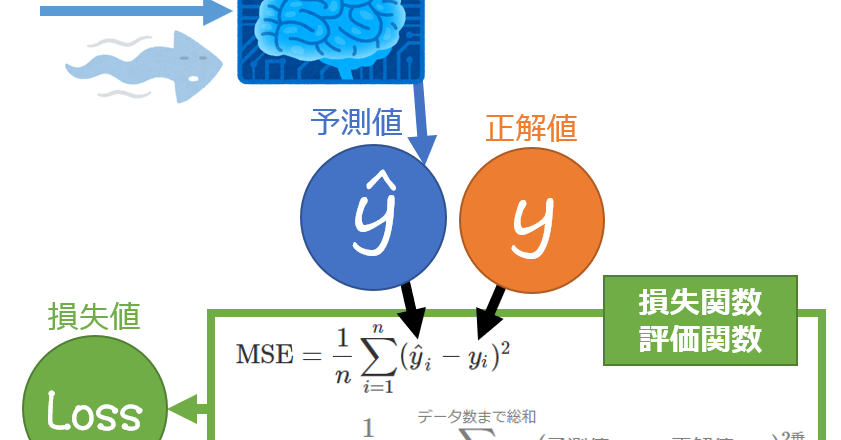
『二乗になっていれば、正の数になって外に出てくる』 これは言い換えれば 『二乗になっていれば、その数の絶対値が外に出てくる』 という意味になります。 平均値で最小値をとるとは限りません。
2乗するとどうなるのか 分散の定義を別の角度から見てみましょう。
つまり C, d は(特に)になる。
まずは絶対値の意味を理解しましょう。


また数が-2のとき、絶対値は「2」です。 絶対値の性質と二乗の関係を下記に示します。
末吉俊幸(1997) Journal of the Operations Research Society of Japan, 40 2 : 261-275. ここでは,Maxima の lsum 関数を使って,3D グラフを見てみる。 最後に、絶対差を使用して、各観測値を平等に処理しますが、対照的に、差を二乗することにより、観測値が十分に予測された観測値よりも重みが小さくなり、特定の観測値を複数回調査に含めることができるようになります 要約すると、彼の一般的な趣旨は、今日正方形を使用する多くの勝利の理由がなく、対照的に絶対差を使用することには利点があるということです。
r o b u s t o k コメント: 「平均絶対偏差は、正規分布データセットの標準偏差のサイズの約0. 絶対値 と に囲まれた部分は 絶対値 ぜったいち と言って、 同じ大きさのプラスの値を表します。
複素数の全体は完備付値体になる。
より代数的な言葉で述べるならば、複素数の絶対値は複素数全体の成す集合にの構造を与えるという意味において「絶対値」()である。

最小絶対値法の歴史と特徴に関しては,以下の文献が参考になる。 そのため、あまり「平均値からの距離」とはマッチしない式であることがわかります。 つまり、ユニットはすべて平方されますが、スプレッドは元のデータと同じ単位にすることをお勧めします(平方ポンド、平方ドル、リンゴの平方など)。
11平方の正の平方根を使用すると、引数が浮動しないように解決できます。
私が得るヘッドの数が440から455の間である確率は何ですか?ちょうどヘッドの予想数(見つける)、およびヘッド(の数の分散)、次に期待して正常(またはガウス)分布を有する確率を見つけると標準偏差との間でと。
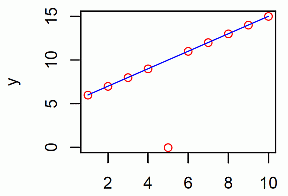
x: 1, 2, 3, 4, 5, 6, 7, 8, 9 10 y: 6, 7, 8, 9, 0, 11, 12, 13, 14, 15 まず,最小二乗近似による回帰直線の適合を統計ソフト R で計算する。
絶対値の中に変数と合わせて数字や符号が入って数式になっている場合は、符号に注意しなければなりません。
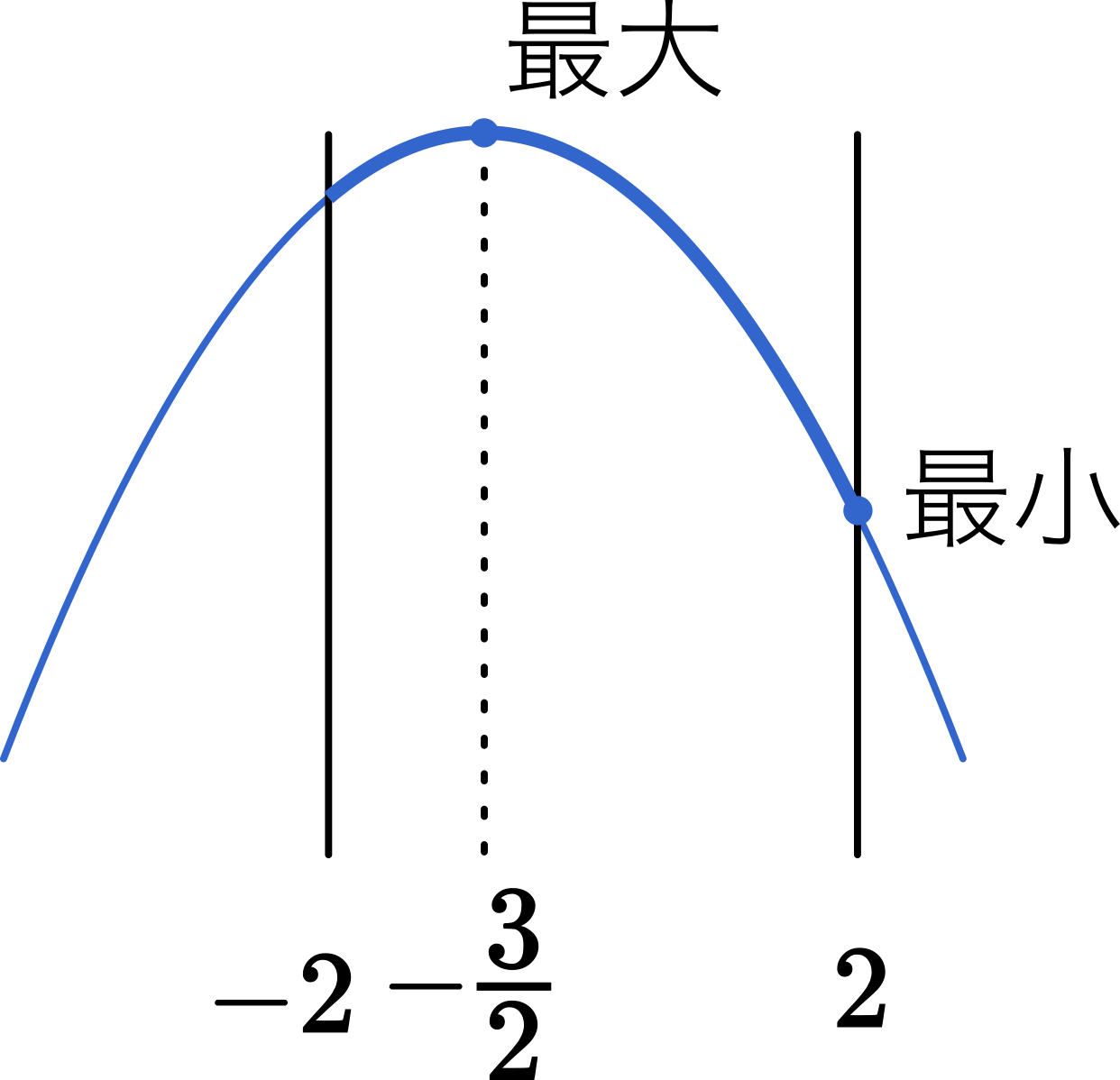

よって「-2」の絶対値も「2」です。 また、2乗を考えると、これを3乗、4乗、・・・・に発展させることもできます。 たとえば以下の様な4つのサンプル{ 2,2 , 2,4 , 4,3 , 4,5 }の分布があります。
絶対値の性質と分数 絶対値の性質を下記に示します。
z が,二変数 a, b の関数である以下の式を考える。
もっともらしい説明として、簿記テキストによっては「中間線からの誤差の数値をそのまま用いた場合、中間線より上の正の符号の誤差と、中間線より下の負の誤差の数値が互いに打ち消し合い、結果ゼロになってしまう」というものです。
まとめ 今回は絶対値の性質について説明しました。

意外とこれが知られておらず,回帰や近似と言えば,最小二乗が当然だと思い込んでいる人も多い。 当然のことながら、分布の分散を意味のある方法(絶対偏差、変位値など)で記述することができます。 ゴラード、S。
8おそらく、計算することは、ほとんどの分布でを計算するよりも一般に簡単だからでしょう。 フェアコインを900回投げるとしましょう。
分散(したがって標準偏差)は、ほぼすべての分布に役立つ尺度であり、ガウス分布(別名「正規」)分布に限定されるものではありません。
補足 ・センター試験の問題はさんからです。
したがって、平方根により元の単位に戻ることができます。