ピタゴラス3体問題で遊ぶ


カオスと3体問題• このあとは、そんな難しい部分を乗り越えてでも読んでほしい、本作の魅力をお伝えしましょう。
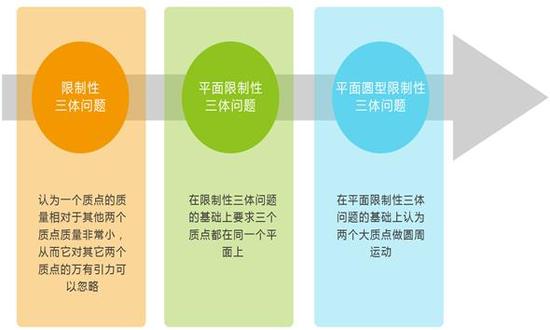
9ただし特殊な制限条件のもとでは解かれており,3つの天体が常に一直線上に並ぶの直線解,伸縮する正三角形の頂点に配列するの正三角形解 ,および周期軌道を与える周期解が知られている。 『三体』の登場人物紹介。
実際その場合は、そういう厄介な部分は一まとめにして何か記号のラベルでも貼っておき、初期条件の変更に際してはそれにかかわる部分だけを分離していじれるわけだから、ある意味で系の振る舞いは一般的な数学的表現がなされていると言って良い。
そうすれば灼熱・極寒地獄に備えて休眠するための時間的猶予を延ばしたり、恒紀中の計画を立てることができるようになる。
ですが、序盤からずっと現実的な理論に基づいた設定が積み重ねられていくので、まったく違和感はありません。

ポアンカレは制限 3 体問題の研究を通じて , このほかにも不動点定理やホモクリニック軌道の発見など , 今日の力学系理論やシンプレクテイツク幾何 の研究の基礎を成すアイデアを得た。
17ところが、数学的に正確に「三体問題は解けない」の意味を説明しようとすると言葉に詰まる。
『三体』の中国語版 思想性とチャレンジ精神が評価のポイント 一方、文章力が批判されても、『三体』シリーズは中国で2200万冊が売られ、高い評価を得ています。
同時に、中国は文化大革命を機に良くも悪くも生まれ変わった、ということが強調されます。
まず第一積分・保存量方式の長所について言うと、こちらの場合先ほど述べたように、第一積分が全部見つかって「解ける」ことがわかった時点で、自動的に解がどの程度の関数や数学的手段で記述できるかもわかってしまうというのが、大きなメリットである。
これは、• それというのも先ほど第一積分の概念を説明するときに、それを「連立一次方程式の拡大版」というイメージで捉えたが、考えてみれば連立一次方程式とはすなわち線形代数のことなのだから、線形代数の延長である作用マトリックスとこれが関係してくるのは、むしろ当然だろう。 しかしそれならば、この「最後のピリオドを打てない」ことを人類の知性の限界として諦めてしまうべきかと言えば、どうも必ずしもそうとは言えないようである。
American Mathematical Society. Piran, Zoe; Piran, Tsvi 2020. 物理学者の 丁儀(ディン・イー)は文潔の娘である 楊冬(ヤン・ドン)の恋人で、宇宙論研究者の彼女が自殺したことから作戦指令センターに協力するようになりました。
三つの天体の運動方程式を立てると、小惑星が太陽や木星に与える引力はごくわずかです。
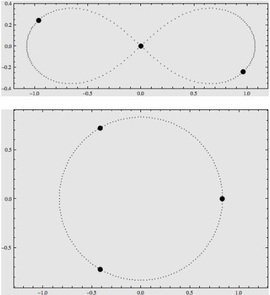
初期位置は重心が原点にくるように配置されています。

この大半が中国人のため、漢字名の読み方が感覚的にわかりにくいというのは、本作を読む上での1つのハードルでしょう。 彼が科学フロンティアに接近したことから、物語が大きく動いていきます。 科学者の一連の不審死。
まずはあらすじ、概要を紹介。
このような、3つの物体の動きを正確に予想できない、というのが三体問題です。
おっと、天体の質量を忘れていた。
昨今の出版界の不況からすれば異例の大ヒットといえます。

すべては文化大革命時代に作られた、紅岸基地に繋がっていきます。 そこでその伝統的なアプローチがどういう思想で行なわれてきたかの要点を、ここで簡単に紹介しておこう。 アルゴリズムの復習 あとで書きます。
2加えて、太陽に近い質量と明るさのA-Bに対してCは赤色でずいぶん小さく暗いというのも作中との三太陽との明らかな差異となっている。
参考文献では補外法と、物体が接近したときに「正則化」という方法で別の微分方程式に 変換して解いてるのですが、難しかったので(汗)、ルンゲクッタ法で、接近したときだけ 計算間隔を小さくする方法で逃げています。
三体問題では,天体をすべて質点とみなすので,天体間に働く万有引力が簡単に表せるかわりに,天体どうしはいくらでも接近できることになり,したがって距離の2乗に反比例する天体間の万有引力はいくらでも大きくなる。
ある問題は、変数(あるいは自由度)の数だけこうした 第一積分・保存量が存在しているならば、次々に変数の中身を書き下していける、つまり「解ける」ということになる 三体問題• そして以上の議論をまとめて、あらためてその意味を言葉にすれば、それがすなわち先ほどの問いへの答えとなる。

オリジナルでは中国の社会的反発を考え合わせて、ストーリーの順序が作者の本来の想定とは変えられていましたが、英訳版以降は正しい形に戻されています。
15この問題については1960年に Sitnikov が制限三体問題に(現在として知られる配位において)振動運動解が存在することを証明し、その後 Alekseev 1968 , Saari and Xia 1989 といった研究を経て Xia 1994 が平面三体問題において振動運動解の存在を証明した。 そしてこの場合言うまでもなく、右辺の列ベクトルの中のa,b,c,・・・の値がちゃんと全部(つまり変数の個数と同じだけ)与えられていることが、解を一挙に書き下せるための条件である。
そこで一見してわかりやすいように相関図を用意しました。
「変数の数が足りない」件について: KaoZ. サブヘイが解いた論文(上のページのリンク中)。
"The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum. さて、問題をこのように言い替えたは良いが、一見すると今度は「対角化できるものがいくつあるか」ということが新たな難問となって、大して先へは進めないようにも思える。