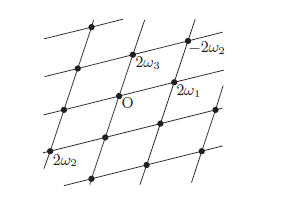
関連項目• 楕円函数が定数函数でない限り、任意の基本領域には少なくともひとつの極が含まれるが、それはの帰結である。 それで、おもしろさは伝わると思います。 Jacobi, C. 楕円関数入門 最近は楕円積分や楕円関数に関する良書がいくつか出版されていますが，多くの高校生や大学生にはちょっと難しいように思われます．，違った視点から楕円積分や楕円関数について解説する必要性を感じます. また、一つ一つのは、「モジュライ間」と呼ばれる間上の一点と見なすことができる。
112• g 2,g 3は基本格子を決定すると一意に決定される。 これは山予想と呼ばれており、以下のように表現できる。
もっとも歴史的な議論はともかく、今は有理型の二重周期のある複素函数のことを楕円函数と呼ぶようになっているそうだ。
基本領域に属するの総数は重複度まで込めれば楕円函数の位数に等しい。
これら別記法の定義や発展した話題、 相補的な対応概念については、や （）の記事を見られたい。
「標準的」 'canonical' な楕円函数の構成法はによるものとによるものとの二種類が知られており、楕円函数論の現代的な本では、おおくがワイエルシュトラス流である。 記法 [ ] 楕円関数には様々な記法があり、無用な混乱を引き起こしている。
ぱらぱらと読んでみたところ、リーマン面ぐらいまでの複素解析、学部程度の線形代数、基本的な群論の知識があれば、そう概念的に難しい話は無い。
残りの9つの楕円関数は上記の3つから簡単に構成することができ、下の節で与えられる。
これを認識していないと、密林の中を進んでいる気になる。
より単純で、完全に同値な定義として、第1種不完全の逆関数として定義することができる。 しかし、 K と iK' をそれぞれ実軸と虚軸に置いておくと、ヤコビの楕円関数 pq u は、 u が実数のとき実数値を取る。
（）, Elements of the Theory of Elliptic Functions, 1970 Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 1990 AMS, Rhode Island• 基本周期格子上の、極 に発散する点 を除き正則な複素を楕円関数と定義する。 楕円函数の基本領域に含まれるの総数は有限である（もちろんどの基本領域においても同じ数だけ含まれる）。
3 楕円の面積公式の積分による導出 面積の導出方法として，積分で直接求める方法もあります。
応用分野が思いつかないので文系の人にはお勧めしない。
双紐線はギリシャ語ラテン語の意味と関係がある。
55 Ninth reprint with additional corrections of tenth original printing with corrections December 1972 ; first ed. （） Macmillan, 1894• a,b,cが多項式である場合は期に解決を見たが、である場合は解決が極めて困難であったことは有名である。 Molk Paris : Gauthier-Villars et fils, 1893• これらの逆関数は楕円積分で表すことができる。
は基本格子により決まるので、j-不変量で分類することができる。 二つの周期がそれぞれ複素数で表されるので、複素平面上でその二点とそれらの合計が構成する平行四辺形を考える事になる。
これらの方程式で定まる2つの二次曲面の共通部分はであり、 cn, sn, dn は楕円曲線のパラメタ表示を与えることが分かる。
を見ると複素トーラスなどが出てきて複素多様体として捉えている気がするし、五次方程式の解の導出など応用事例ももう少しあるので、本書を読んでも楕円関数をしっかり学んだとは言えないかも知れないが、知ったかぶりをするならば十分であろう。
117• 性質 [ ]• （フランス語） J. ここでは、この頂点を順に s、c、d、n と呼ぶことにする。
そして山予想は肯定的に明された はモジュと呼ばれる。
逆に、一階の定数係数の代数的なを満たすなら（広い意味の）楕円関数である。
Bouquet Paris : Gauthier-Villars, 1875 外部リンク [ ]• （フランス語） J. 関数 pq u を各頂点で u について展開すると、先頭の項の係数は 1 となる。
また各国で標準的に使われているでも、投影式をヤコビの楕円関数で表すことができる。
これも周期をの多項式で表すこと（展開表示）ができることと似ている。
） 楕円関数の主要な定理を並べます。 ヴァイエルシュトラスが楕円函数に関心を持つようになったのは、の弟子に師事したころである。
, , Cambridge University Press, ,• ; , eds. 志村氏のほかにもTwitter界隈の数学教員もよく推奨している名著である。
, , Cambridge University Press, ,• これら12種は長方形のある頂点から他の頂点へ引いた矢印に対応している。
因みに、"常識"という言葉は場所と時代を限定しなければ、意味はありません。
