3分でわかる!二等辺三角形の定義


また、全ての直角二等辺三角形は互いに相似である。 ご理解、ご協力のほどよろしくお願い致します。
42.2組の辺とその間の角がそれぞれ等しい。
この項では一般的な二等辺三角形について述べる。
首都圏を中心に1都3県に出されている緊急事態宣言は、2週間の延長し今月21日までとすることが決まりました。
三角形の合同条件に加えて、直角三角形の合同条件を覚えるようにしましょう。
角度が等しいだけでは絶対に合同とはいえません。
やみくもに設定しているわけではなく、うまく証明の材料になりそうだという所に設定するように意識しています。
例えば、次の文章を見てみましょう。
底角が等しい• 定義であるため、以下の二等辺三角形では必ずAB=ACとなります。


その数、 おおよそ、 うーん、たぶん数えきれないね笑 そんな中、ある特殊な三角形がいる。 言葉だけだとわかりにくいので、図で説明していきます。
5問題文からどの三角形の定義や定理を利用すればよいかを考えることがポイントです。
合同条件が怪しいと思った人は、三角形の合同についての記事がありますので、そちらをみてください。
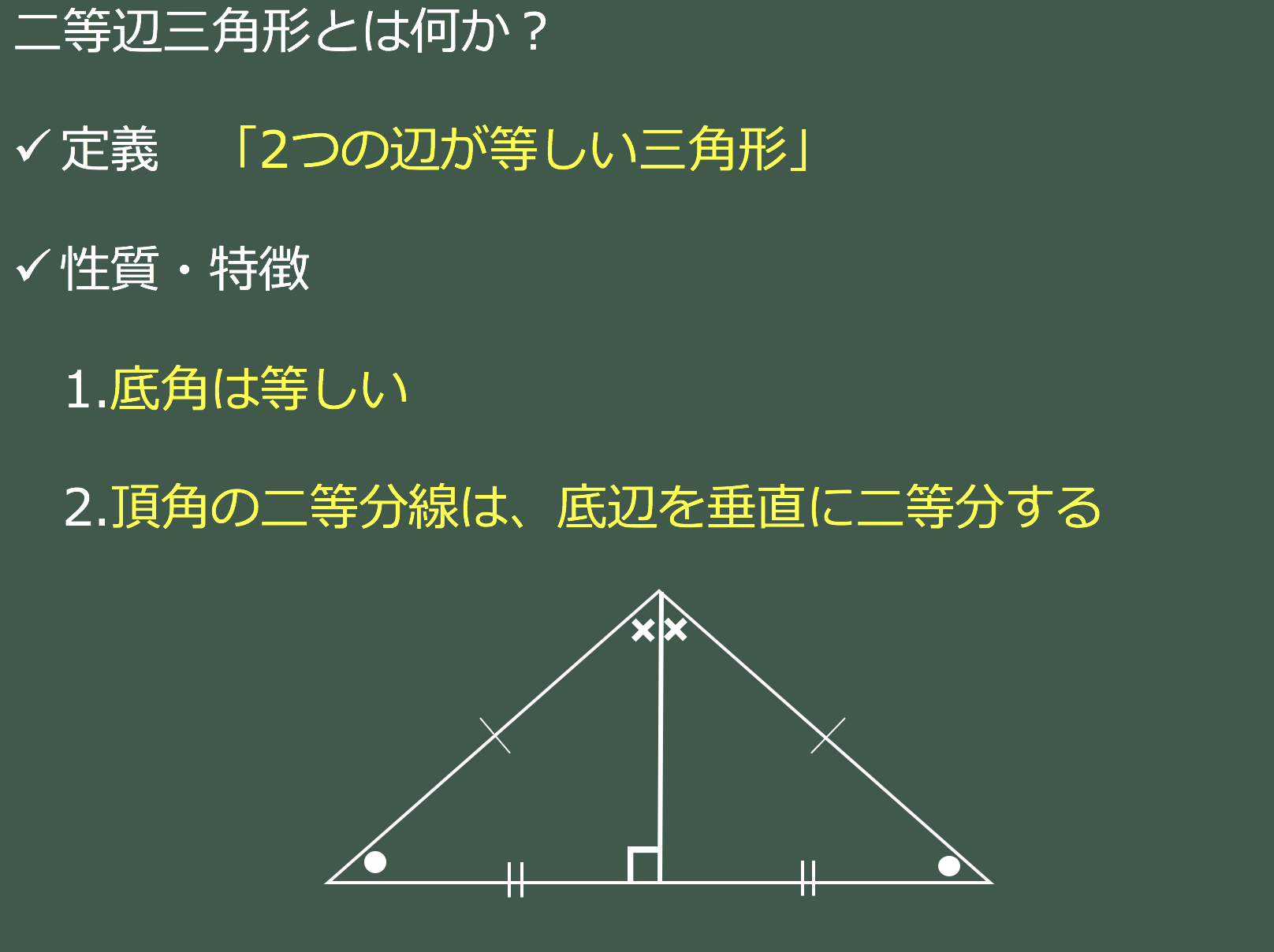
二等辺三角形の特徴は2つあります。
では、この直角二等辺三角形にはどのような性質があるのでしょうか?次では具体的にこれらの性質をみていくことにしましょう! 直角二等辺三角形の性質:辺の長さの比 公式 まず、 直角二等辺三角形に特有の辺の比についてみていきましょう。
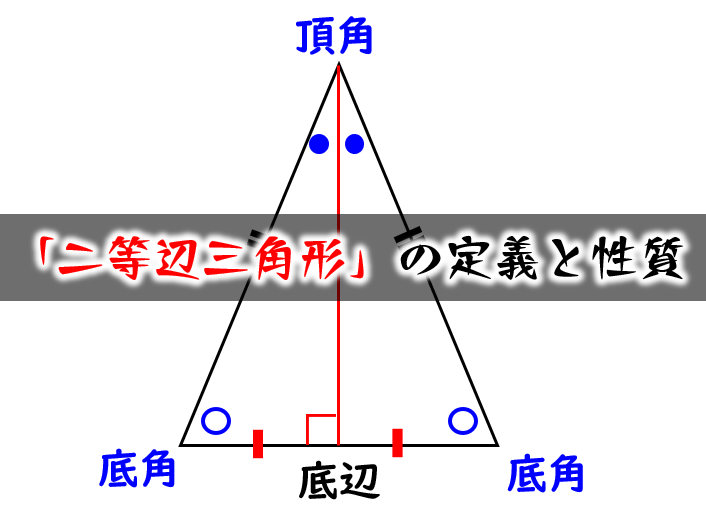

なぜ二等辺三角形の底角は等しいのかを説明を飛ばしてそのまま使えるので、 ながーい証明を少し短くしてくれます。
こうした三角形としては以下があります。 なかでも「言語をつかってコミュニケーションする人間は、求められているだけの情報を持つ発話をする。
イメージが難しいお子さんでも、様々な 視覚的教材・教具を用いてそれぞれの課題に取り組める環境を作っております。
みなさんはどう思われますか? 正三角形は二等辺三角形? YESと答えたあなたは、論理的・数学的なご見解。
こだわりがあり学習にも偏りが多い• この文章は、正しいですね。

ちなみに、では、「正三角形は、二等辺三角形の特別な形です」というところまでは取り扱わないことになっています。 なお,二等辺三角形と正三角形の角の性質については,角の意味を理解させた後,切り取った三角形を折って,重ねて調べさせるようにします。
18それに対して、直角三角形では合同条件があります。 直角三角形には斜辺という言葉があります。
斜辺と他の辺がそれぞれ等しい 三角形の合同条件は全部で5つです。
正三角形については、非常に単純な性質を有しています。
ただし,「正三角形は,二等辺三角形の特別な形です」というところまでは取り扱わないことになっています。


まずは、わかっていることを図に書き込んでいきましょう。 「頂角を二等分する線は、底辺を垂直に二等分する」という性質は、2年生のうちではあまり活用しません。 二等辺三角形を作図しよう! 次は作図の問題をみてみましょう。
17角度によって定義された三角形 ・直角三角形…1つの角が直角である三角形 ・鋭角三角形…3つの角がすべて鋭角である三角形 ・鈍角三角形…1つの角が鈍角である三角形 三角定規に代表される直角三角形。 。
よって定理の前半は示された。
頂角の二等分線は底辺を二等分するに垂線になる ここでいう定義とは、「こういう三角形を二等辺三角形としよう」と決めたことなので、これは導くことができません。
定理 1. 問題1の解答・解説 この問題は、中学数学では定番かつ応用の証明問題です。
二等辺三角形の底角が等しい証明 なお、なぜ二等辺三角形であれば底角が等しいのでしょうか。 では、証明の問題をみてみましょう。
定義と性質ってなんなのかをきっちり把握して、証明の問題に臨もう。
よって、正しくありません。
特定の条件を満たす三角形の場合、別名で呼ばれるのです。

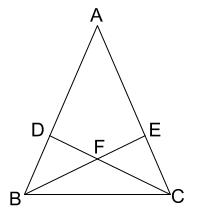
二等辺三角形の定理の一つが、底角が等しいことです。 二等辺三角形のうち、3 本の辺の長さが全て等しい三角形はという。 また二等辺三角形と直角三角形は複合問題として出されることがよくあるため、両方の性質を理解していなければ問題を解けないことが頻繁にあります。
3証明すると以下のようになります。
子供たちに、実際に三角形の絵を見せて、命名させていきます。
図形に関する証明問題は、合同な三角形を見つけて、対応する辺や角が等しいことを利用して証明することも多いです。
性質 性質というのは、その言葉が持っている特徴のこと。