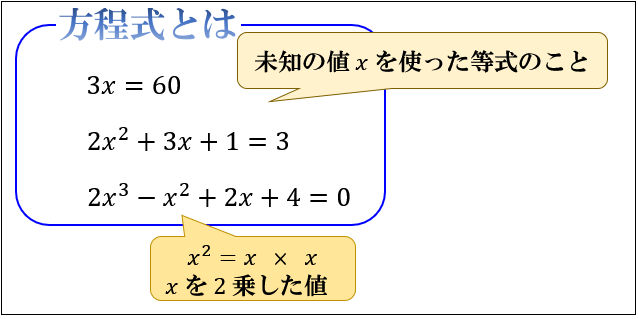
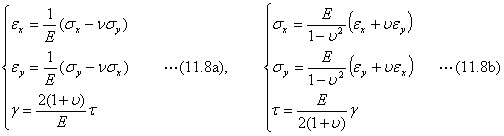知ってる?「一次元」と「二次元」と「三次元」と「四次元」の違い


2次元配列の軸を入れ替え 例として、先ほどの2次元配列の軸を入れ替えてみます。 transpose 2 , 1 , 0 array [[[ 0, 12], [ 4, 16], [ 8, 20]], [[ 1, 13], [ 5, 17], [ 9, 21]], [[ 2, 14], [ 6, 18], [10, 22]], [[ 3, 15], [ 7, 19], [11, 23]]] さいごに いかがでしたでしょうか。