Pythonを使って、2021を素因数分解する

右の列の素数に達するまで、時々最小素数を探して部門に進みます。 これは、奇数の因子が負でなければならないことを意味します。
18では、こんな面倒くさい素因数分解を何に使うのという疑問が湧きますよね。 2027と2029のペアは双子素数ですから、双子素数年となります。
最後までお付き合いいただき、ありがとうございます。
ある一つの解法で魔法のように解ける問題などを当てにして合格を狙っても面白くありません。
もちろんこれを筆算でやっても良いですが、中3の式の因数分解を学習済みならこうしましょう。


p, q がそれぞれ一部わかっている例 dが同じでnやeが異なる暗号文 Small Common Private Exponent かつ、dがある程度小さければSmall Common Private Exponent Attackができる。
18整数問題を解く時の基本ですね。 出題例• 4)与えられた数がステップ1の素数で割り切れる場合、答えは合成または素数でしたか?合成する場合、この番号を使用し、ステップ1〜3を素数2から繰り返します。
2021年の開催ですが、大会名は東京2021ではなく、東京2020のままで行われると決まっているようです。
西暦の年数が問題に出てくることがある ほとんどの整数は、1桁または2桁の合成数ですから、せいぜい計算しても3桁です。
掛け算九九の範囲以外でも、10の倍数の平方は簡単に出せますね。
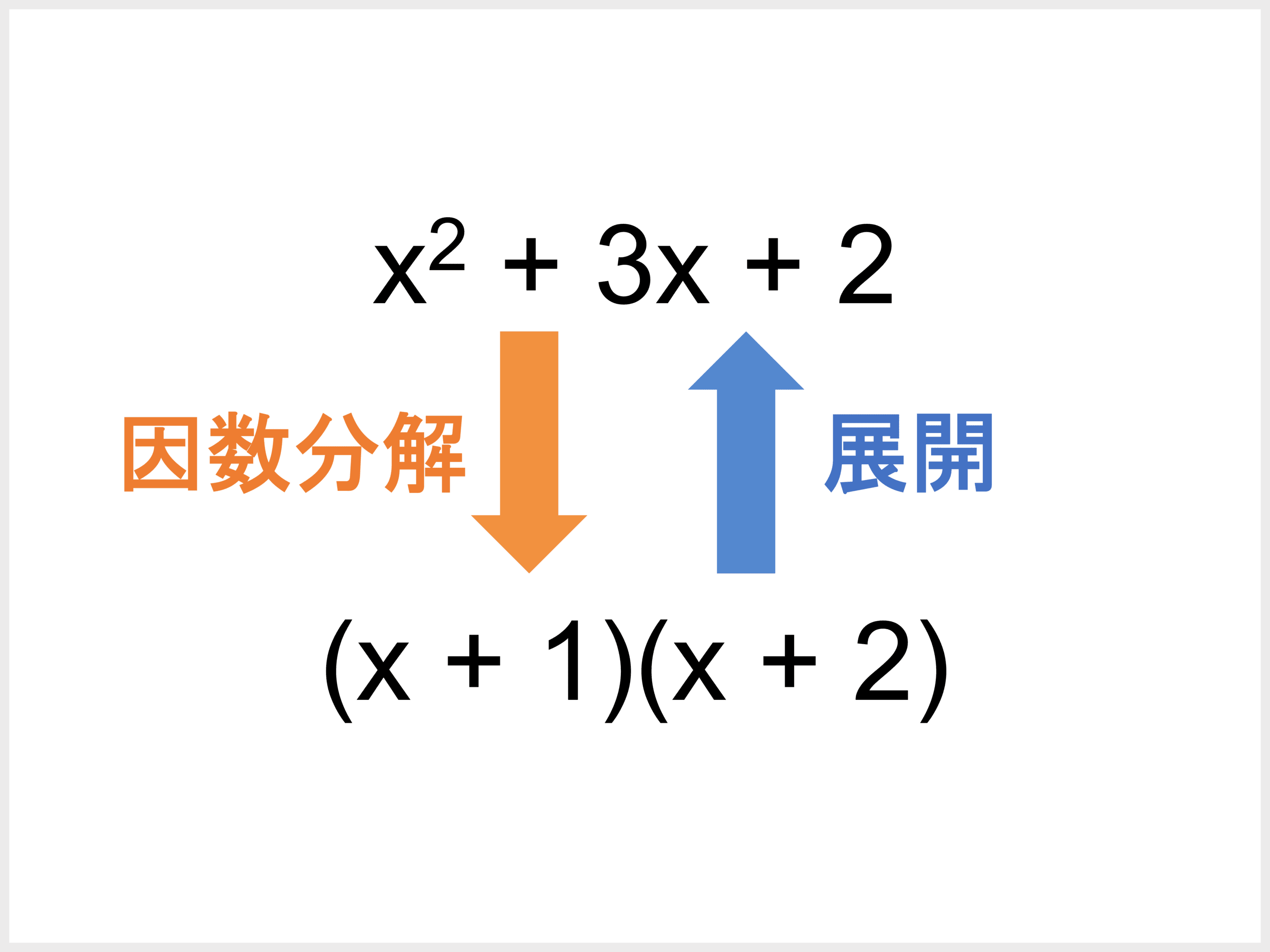
問題2 (部分分数分解の問題) これは、結局素因数分解をしないといけないんですけど. 6年上級者の方どうぞ。 また、暗記レベルで言えば11~14の平方は非常によく見かけるので覚えておいてください。 各整数は、他の2つの整数の積として書き換えることができます。
7素因数分解は、最小公倍数と最大公約数を見つけるために使用されます。
257,887pv 高校で習う微分と積分は、数学の中でもかなり高レベルな内容です。
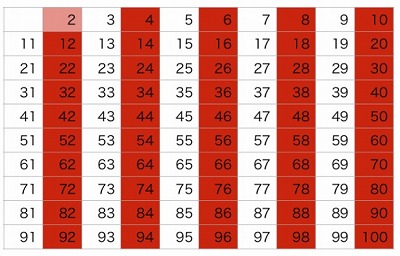
738• 次に小さくふるい落とされていない数字を取り出し、上記を繰り返す。
素数の発見法 エラトステネスのふるい 上記のように割り算していき、もし割り切ることができなければ、2021は「素数」となります。

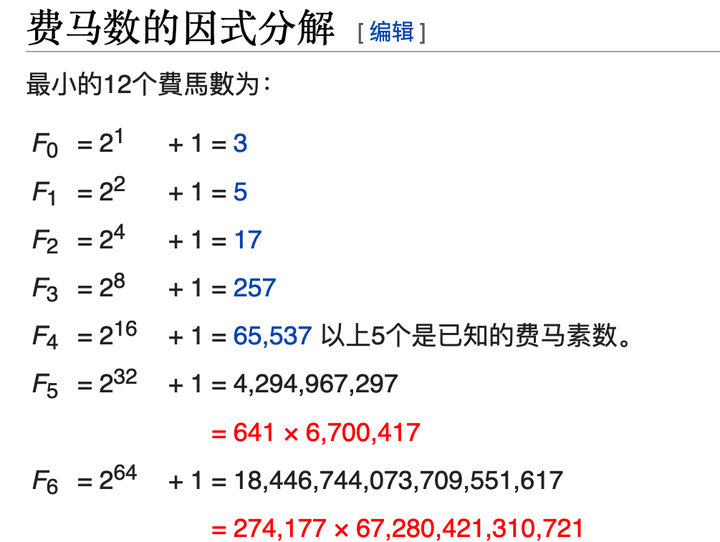
実際これは効率的に結果を得るうえで正しい方法だと思います。 という並びがあります。 3が素数であるのは、その唯一の因子が1と3であるためです。
さて、来年は令和3年の西暦2021年。 こういうケースがある、またこういう場合はどうすればよいのかという情報や質問をお待ちしています。
一方で でれば、復号結果は となるから( )偶数と奇数の減算で奇数になる。
2,3,5,7,11,13,17,19,23,29,31,37,41,43 でチェックすることになります。
素数 素数には2つの要素しかありません。
まえがき みなさん競技プログラミングをはじめて、割と最初のほうに自分専用ライブラリづくりをされるかなと思います。 出題例• 問題の番号を書きます。
たとえば、17の係数は1と17のみです。
このロジックに従ってください。
黙って や を読んでおけば大体なんとかなる e が 3など Low Public Exponent 例えば、 であればe乗根を取ることで が手に入る 出題例• 僕もしました。
sageに実装されているCoppersmith methodは一変数に対するものだが、多変数に対してはdefundさんが実装しているものが出来がよく、これを使っておけばだいたいなんとかなる。
297• たとえば、1、2、3、5、7、11、13、および17はすべて素数です。 ということで、2021がきれいに素因数分解できました。
一の位から2の倍数ではありません。
1,304• 私も最初はこれは7で割った余りなのかなと直感しましたが、全く違っていました。
ここの動作が遅いようでは、ただの怠け者です。
ところがです、数学オリンピックでもないのに、4桁の数が問題文に出てくることがあります。
1,124• 基本的には、与えられた整数を素数で割っていって考えます。
もう少し絞り込みたいので、45の平方を計算します。
その時点で、最小の素因数が見つかりました。
平方数を頼りに見当をつけても、それより遠いところに因数があることだってごまんとあります。
以前に解けるソルバを作ったので使い方を憶えると解きやすくなるはず 出題例• これがあればいろんな数学的に必要な概念をコードにするときにめっちゃ楽やん! というか、そもそも数学知識が無いとすることになりますから(経験談)、どのみち考えても大してうまくいくわけないしこうやってちゃんとしてそうなコードを写経するのは遅かれ早かれ必要になるんですよね。
2021 この記事の内容:基本的な整数を因子に分解する大きな数を分解する手順 ザ・ 要因 数のとは、数を掛け合わせ、その数自体を製品として与える数です。
【正解】2581の値は2となります。


偶数である6552の例に戻ると、2が最小の素因数であることがわかります。 Coppersmithも内部ではそれっぽい格子を生成してLLLをしているのでどちらでも解ける。
8さらに、「約数」とは「指定された数を割り切る数」を意味します。 2021という数字に着目してみましょう。
では、今年の西暦である「2021」を素因数分解してみましょう。
A いっぱい これは、小数部または小数部のない数値です(すべての整数は負でも正でもかまいません)。
p 以外の p の倍数を全て消す。