立方体の表面積の求め方は?1分でわかる計算、公式、直方体の表面積の求め方

一辺の長さが2cmですね。
9A:平面上の直線の位置関係と比べながら,平行・垂直になっている面を考えることができる。 B:直方体の面の形や辺の長さ,面と面とのつながりを考えて展開図をかくことができる。
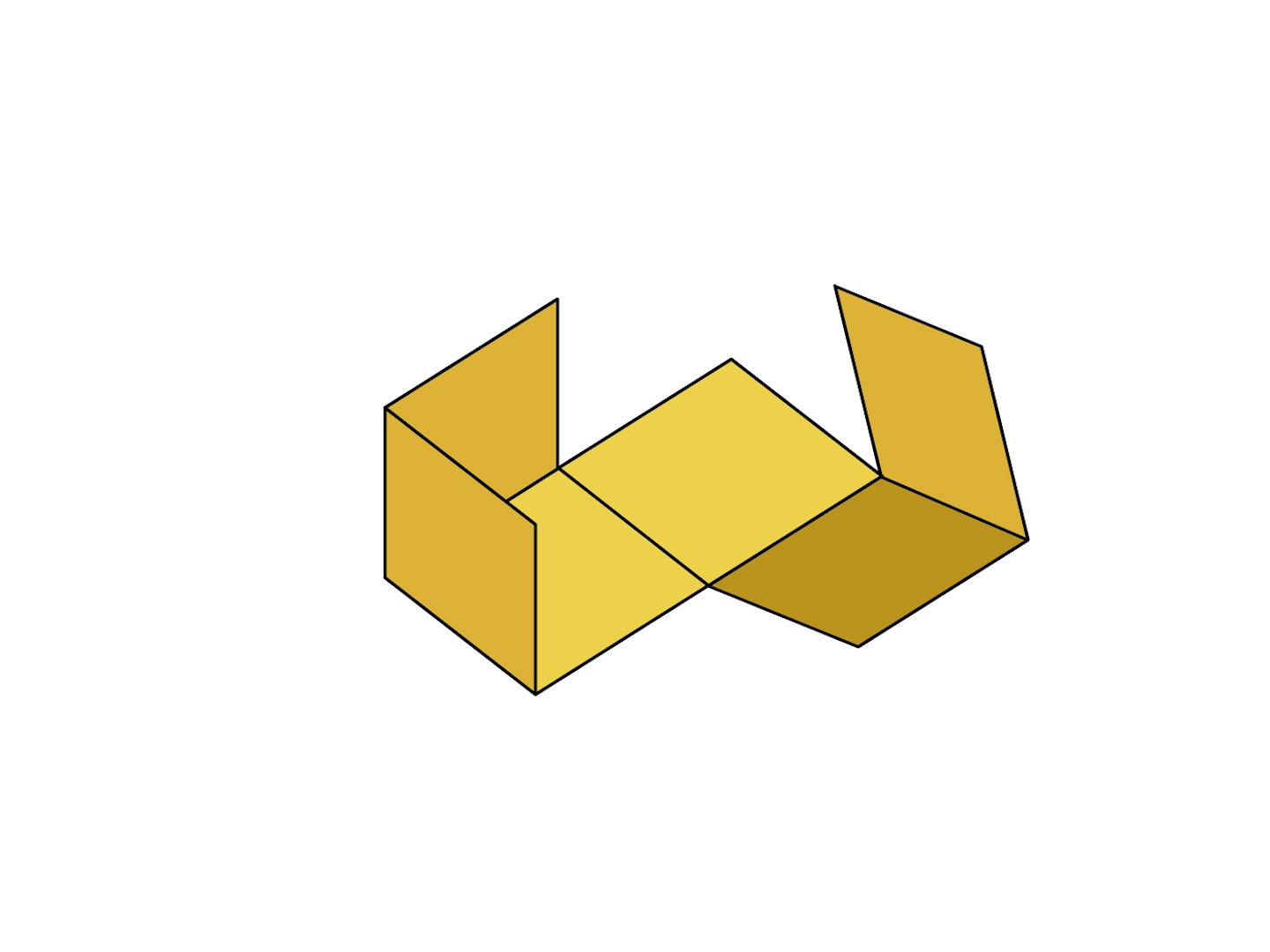
4 5 cmの立方体の切り開く活動を通して,立方体のいろいろな展開図を考える。
A:上記に加え,直方体や立方体の形は1つの頂点に集まっている,縦,横,高さの3つの辺の長さで決まることが分かる。
正方形だけで囲まれた形を 立方体といいます。
立方体とは一辺の長さが全て同じで、6つの面から構成される立体図形です。 あとは前述した式に代入すればよいです。 これらはの第4段の2、3番目の数字に等しい。
171つの頂点を共有する辺どうしは垂直に交わるが、接点を持たない辺どうしは平行な関係にある場合と互いににある場合の2パターンがある。
サイコロの形と説明します。
なお、表面積の意味、立方体の詳細は下記が参考になります。
直方体の一種であるため、、、の一種でもある。

_P1_6imH7Pg0_.jpg?1486330065)
直方体は6面の長方形で構成されます。 A:Bに加え,展開図から辺と辺の重なりや点と点の重なりを考えることができる。 直方体の詳細、立方体の表面積、表面積の意味など下記も勉強しましょう。
4練習問題 下の形を直方体と立方体に分けましょう。
おかしの箱の形と説明します。
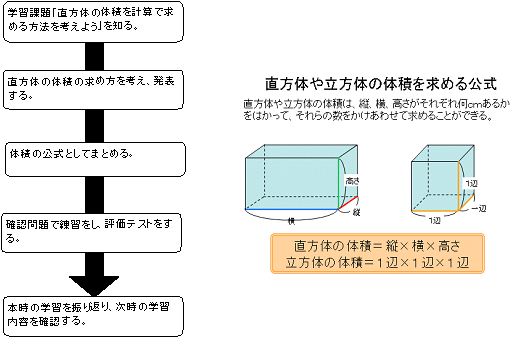
第4学年 算数科「直方体と立方体」評価規準 単元の評価規準 算数への関心・意欲・態度 数学的な考え方 数量や図形についての技能 数量や図形についての知識・理解 立方体や直方体を身のまわりから見つけたり,これらの立体図形の性質を進んで調べたりしようとする。
下式の通り、立方体の表面積は、一辺の長さの2乗を6倍した値です。

また、Cには直方体の構成要素だけではなく、辺や面のつながりや位置関係について多面的に捉えて展開図がかけたことを称賛します。 面の形は、長方形だけの場合と長方形と正方形がある場合があります。 (直方体の性質)•。
14Aのように「3つの辺の長さを足した長さが長いほど立体は大きい」と考えたり、「展開図が広い(表面積が大きい)ほど立体は大きい」と考えたりする子供は少なからずいます。 イかウかは分からない。
5 直方体において面と面の平行・垂直の関係を理解する。
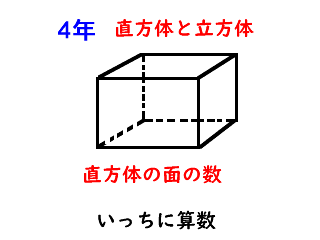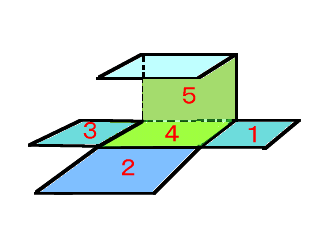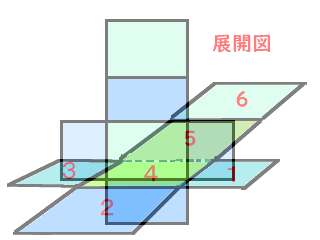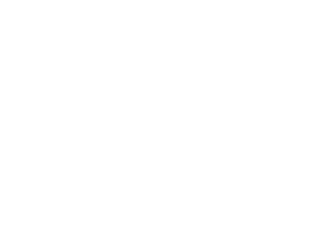
3 直方体や立方体の展開図のかき方を理解する。
立方体や直方体を点,線,面の構成要素から分析的にとらえ,それを基に立体図形の構成を考える。

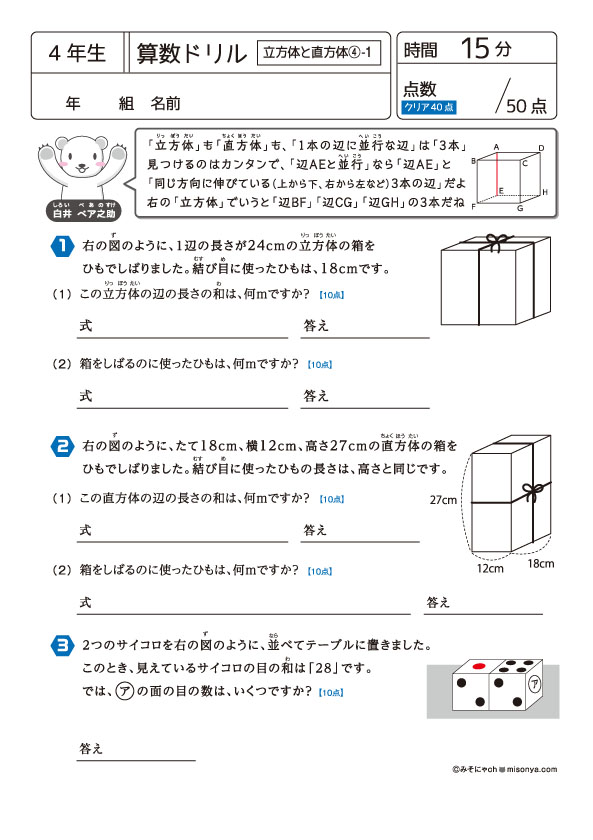
頂点 ちょうてん は、直方体も立方体も8つあります。 このように、面と面や辺と辺の位置関係やつながりに着目すれば、どんな形の直方体の展開図もかけそうだという考え方を押さえることが大切です。 4年「平行と垂直」のおさらいをすると 面や辺の平行と垂直の関係が わかりやすくなります。
4直方体・立方体の部分について 直方体も立方体も角の部分を頂点と言います。
問題 上の箱と似ている形を、下の中から選びましょう。
実際に、下図に示す立方体の表面積を計算しましょう。
これらのことから「向かい合う面と面の大きさと形が同じになる」または「隣り合う面のくっつき合う辺の長さは等しくなる」ということをまとめます。
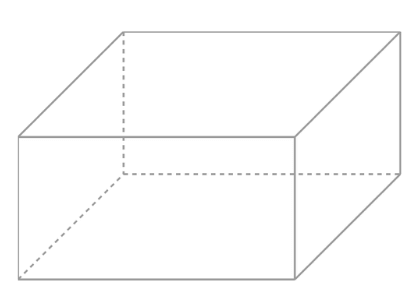
表面積は立体図形の表面の面積の合計です。 直方体や立方体などの全体のが わかるようにかいた図を 見取り図(みとりず)といいます。 展開図がかけたら箱を組み立てさせ、正しく直方体ができたかを確認します。
直方体の表面積の求め方と例題 例題を通して、直方体の表面積を求めましょう。 イとウ」 ・辺の長さから考えている子 B 素朴に解いている子 ア、イ、ウを重ね、アが小さい。
学び合いの計画 展開図をかく際に、どのように考えたのか、図と言葉を使って説明させます。
直方体と似た立体に「立方体」があります。
B:概ね 似ている立体を見つけることができる。
C ねらい通り解いている子 向かい合う面と面、くっつき合う辺の長さを基に展開図をかき、説明することができる。 よって立方体の表面積は です。
向かい合う面どうしはであり、隣り合う(接する)面とは互いにに交わる。
具体物を提示することで、面や辺のつながりが捉えやすくなります。
B 素朴に解いている子 向かい合う面と面、くっつき合う辺の長さのどちらかを基に展開図をかき、説明することができる。
よって、 となります。 立方体の表面積の求め方は6a 2です(aは立方体の一辺の長さ)。
10 3次元座標の見方を理解し,座標を読んだり,座標を使って位置を表したりする。
直方体の体積、表面積の意味など下記も勉強しましょう。
・下の図のように,箱の形を辺のところで切って,平面の上に広げてかいた図を, 展開図といいます。