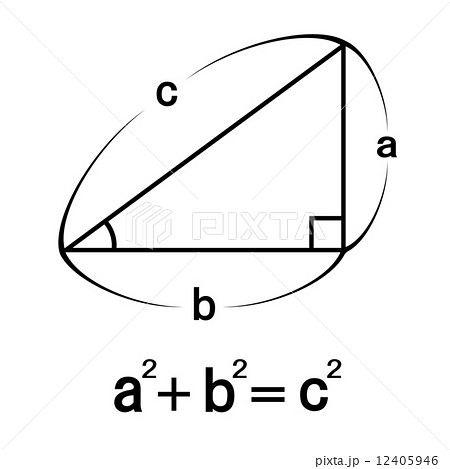
ピタゴラスの定理とは?1分でわかる意味、証明、3:4:5の関係、三平方の定理との違い

「三平方」なので、3つの値の平方をとる、という意味です。 The Mathematical Intelligencer. 1 直角三角形で、正方形以外の別の形でいえないか 原型を「くずす」「はずす」「ずらす」(メタモルフォーゼ)という発想です。
14

「三平方」なので、3つの値の平方をとる、という意味です。 The Mathematical Intelligencer. 1 直角三角形で、正方形以外の別の形でいえないか 原型を「くずす」「はずす」「ずらす」(メタモルフォーゼ)という発想です。
14Interactive Mathematics Miscellany and Puzzles. According to one legend, ca. From at Clark University• Proofs by dissection and rearrangement We have already discussed the Pythagorean proof, which was a proof by rearrangement. ここで、ピタゴラスの定理の拡張を例にして、数学における拡張から発見する方法を考えてみます。
実は「面積の等しい二つの多角形は、一方を有限回分割して組直すことで、他方の多角形と合同な多角形を作ることができる」という定理があり、切り方も何通りもあることが分かっています。
それをもとに「ピタゴラスの定理」を証明する。
KAの延長とFBの延長との交点をLとし、また、DからALに平行にDMを引き、EからBLに平行にEMを引き、その交点をMとする。

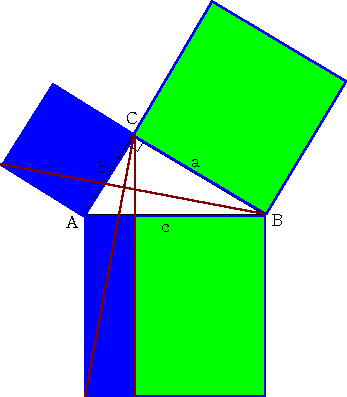
さらに小さな正方形(黄色)も、それぞれ赤の正方形と同じ面積になるはずなので、黄色の面積の合計は始まり正方形と同じであることがわかります。 しかし、 65,119,180 のように、ピタゴラス三角形の組み合わせではできないヘロン三角形も存在します。 The Pythagorean identity can be extended to sums of more than two orthogonal vectors. These form two sides of a triangle, CDE, which with E chosen so CE is perpendicular to the hypotenuse is a right triangle approximately similar to ABC. というピタゴラス数が得られます。
1a, b, c を原始ピタゴラス数、 n を自然数とする。
The underlying question is why Euclid did not use this proof, but invented another. TからACに平行にTSを引く。
Those two parts have the same shape as the original right triangle, and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. 四角形 A C B D ACBD A CB D の面積 S S S を二通りの方法で表す。
a の順序はの数列 による。
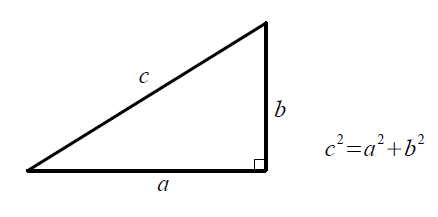

For example, a may be considered as a with infinitely many components in an inner product space, as in. 直角三角形の面積はである。 下記にピタゴラスの定理を示しました。 The formulas can be discovered by using Pythagoras's theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. 32: The generalized Pythagorean theorem". "Pythagorean 'Rule' and 'Theorem' — Mirror of the Relation Between Babylonian and Greek Mathematics". 証明4 合同な図形を巧妙に利用する証明。
3きれいに移動させることができたら、「もう1セット」作っておいた4つの三角形を、最初と同じ様に(図の左側)、もう一度並べてみましょう。
ピタゴラスの定理の簡単な証明 ピタゴラスの定理を証明します。
Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. it is not until Euclid that we find a logical sequence of general theorems with proper proofs. The New England Journal of Education. 国立国会図書館• ピタゴラスの定理を、対辺の積と対角線の積に変えても成立します。
An extensive discussion of the historical evidence is provided in , p. 3,4,5 が一番よく知られたピタゴラス数ですが、他に 5,12,13 や 15,8,17 などもピタゴラス数です。
Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. (ちなみに、教団に入るためには、全財産を寄付し、俗世を断つ必要がある) その中で生まれた「 ピタゴラスの定理」こと「三平方の定理」は 「 直角三角形の斜辺の2乗は、他の2辺の2乗の和と等しい」 という直角三角形の3辺の関係を示したものだ。 lemma 2• The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c. , 1968 があり、この本は米国ERIC Education Research Information Center の電子図書館 で読むことができます。
3"The Pythagorean proposition: A proof by means of calculus". そして、PとAを結ぶ。
3 となる。
If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent. 長方形を作ると二つの合同な直角三角形ができます。
次に、これらの4点を通り、BCあるいは、ACに平行にPW,QT,RU,SVを引く。

図1のように1から5を定める。
の時点ですでに上において本定理の成立が明らかである。
Euclid's Elements: Book VI, Proposition VI 31: "In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle. Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts. , writing in the fifth century AD, states two arithmetic rules, "one of them attributed to Plato, the other to Pythagoras", for generating special Pythagorean triples. Combining the smaller square with these rectangles produces two squares of areas a 2 and b 2, which must have the same area as the initial large square.。
シルヴァーマン, ジョセフ・H『はじめての数論 発見と証明の大航海 ピタゴラスの定理から楕円曲線まで』鈴木治郎 訳、丸善出版、2014年5月、原著第3版。
[裏話] 当時、ピタゴラスの学校というものは、現代の学校と違い、閉ざされた集団でした。
Such a triple is commonly written a, b, c. The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. The view of Pythagoras's cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus. The proof of similarity of the triangles requires the : The sum of the angles in a triangle is two right angles, and is equivalent to the. 99-101, 147-149• 三平方の定理(ピタゴラスの定理) 関連ページ 三角形、平行四辺形、ひし形、台形、正六角形、円、扇形、楕円などの平面図形の面積を求めるときに使う公式についてまとめています。 例えば、三角関数を用いて表わすとどうなるのでしょうか。
また、図1のように1から5を定める。
"On generalizing the Pythagorean theorem", The College Mathematics Journal 34 4 , September 2003, pp. Pythagoras's theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the operation. また構造力学や構造設計でも、ピタゴラスの定理を使い、材の長さや内力の計算をします。
『ピタゴラスの定理』東海書房、1952年。


Archived from PDF on 2021-02-26. A simple example is Euclidean flat space expressed in. This proof, which appears in Euclid's Elements as that of Proposition 47 in Book 1, demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares. よく見てみると、一部の形が全体の形に似ています。 The theorem can be in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids. " is an Old Babylonian clay tablet from concerning the computation of the sides of a rectangle given its area and diagonal. Then two rectangles are formed with sides a and b by moving the triangles. ピタゴラスの定理とその証明 ピタゴラスの定理とその証明 中学3年で学習するピタゴラスの定理(三平方の定理)は、その後の数学の学習で繰り 返し用いられる重要な定理である。
20KHの延長とFGの延長との交点をLとする。
この事実から、ピタゴラスの定理を用いて任意の2点の間のを測ることができる。
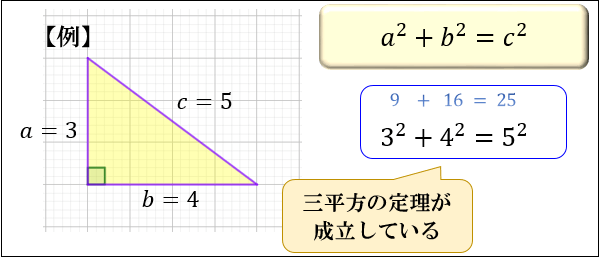
今回はピタゴラスの定理の意味、定理の証明、3:4:5の関係、三平方の定理との違いについて説明します。
例えば、において原点と任意の点を結ぶ線分の長さは、ピタゴラスの定理に従って、その点の座標成分を2乗したものの総和の平方根として表すことができる。