微積分学の基本定理

また,「分割を増やす」ボタンをクリックすると,分割数を1ずつ増やすことができます。 微分法の用途としては、やに関わる計算、曲線の接線の傾きの計算、の計算などがある。 この同じストリップの面積 を 推定 する 別の方法があり ます。
18
また,「分割を増やす」ボタンをクリックすると,分割数を1ずつ増やすことができます。 微分法の用途としては、やに関わる計算、曲線の接線の傾きの計算、の計算などがある。 この同じストリップの面積 を 推定 する 別の方法があり ます。
18d t。
5世紀にはが後にと呼ばれるようになる方法を使っての体積を求めた。
一般化 区間全体 で fの 連続性を仮定する必要はありません。
距離の情報(ある時間にどの位置にいたか)がわかっていれば、特定の瞬間における速度を求められます。

その他、符号や積分区間に関する定積分の基本的な規則などについても合わせてこの表でまとめておきます。 ニュートンとライプニッツがそれぞれの成果を出版したとき、どちら(すなわちどちらの国)が賞賛に値するのかという大きな論争が発生した。 これは、 の不定積分の存在を意味し。
13ここまで分割しても,出っ張りはまだまだあります。
05 この記事を読むと分かること ・無理数の相等とは何か ・無理数の相等の証明 ・無理数の相等を使うときの記述の書き方 ・無理数の相等が関わる問題 目次 1[…]• 数量で始まる F ( B )A」 F ( )。
f の連続性により、 後者の式は hと 同様 にゼロになる傾向があります。
Government of Kerala — Kerala Call, September 2004. 記事の最初に確認したイメージを、ニュートンは考えていたわけですね。
古代 は 、 を介して面積を計算する方法を知っていました。
ところで,上の図の最大分割数は100です。
cos x の微分は -sin x なので、「マイナス符号を消す」ために -cos x を考えている事に注意してください。
ここで、パーティションのサイズが小さくなり、 n が大きくなり、スペースをカバーするパーティションが増えると、曲線の実際の領域にどんどん近づいていきます。
は微分積分学の発展に最も貢献した1人であり、万有引力の法則や運動の法則でも微分積分学を応用している。 例えば、ln x の原始関数は、微分の公式集を見ると見当たりません。 (( 私" バツ 私 )。
( 2012年9月) 微分積分学(びぶんせきぶんがく, )とは、の基本的な部分を形成するの分野の一つである。 ただし、2 においては導関数が連続でなくとも成立するので、3 よりも汎用性が高い。
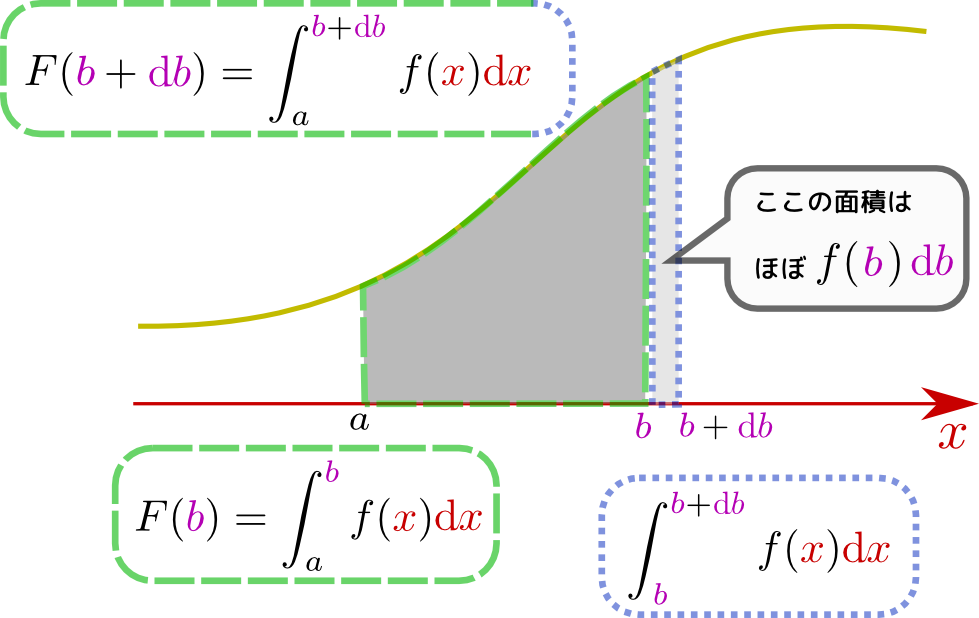
添付の図に示すように、 hに f ( x )を 掛けて 、このストリップとほぼ同じサイズの長方形の領域を見つけます。
つまり、最大のパーティションのサイズがゼロに近づくにつれて制限が適用されるため、他のすべてのパーティションは小さくなり、パーティションの数は無限大に近づきます。
1 三角関数の積分 三角関数の微分はすでに求めてあるので、「微積分学の基本定理」を使えば積分も簡単と言えば簡単なのだが、ここではあえて「足算の化け物」としての定積分としても三角関数の積分を求めよう。
クーラント、リヒャルト; ジョン、フリッツ(1965)、 計算と分析の概要 、Springer。 微分したあとの式からは、元の式の定数項がなんだったかという情報は得られないですよね。
赤のストライプの斜線部は、近くにある H 回 fは ( X )。
しかし、現代に通じる微分積分学は、17世紀ので、とがそれぞれ独立に確立したものである。
積分は複雑な図形の面積を求める方法(求積法)として、微分は運動する物体の軌跡変化(例:砲丸の弾道計算など)を求める方法としてそれぞれ発展していきました。
長方形の代わりに台形で近似すると,収束がもっと早くなります。 微分の公式と比べると、一見簡単な関数の原始関数がやたらと複雑になる場合がある事にも、注意してみてください。
基本的には「微分の逆演算」をやるだけですので、微分と別途に「積分の公式」を覚える必要は、それほどない・・とは、思います。
一方、グレゴリーの思想は、非常に幾何学的な性質を持つ概念フレームワークに属しています。
1 は積分してから微分するとまったく元に戻ることを、2 は微分して積分すると、高々定数の差を除いてもとの関数が現われることをそれぞれ主張するものである。

このページでは述べていない公式や、まだしていない考察も大学数学の微積分学には多く含まれます。 ことがありましょう数字 のx 1 、. 「収束が遅い」といいます。 逆に、定理の第二の部分、とも呼ばれる 歯石の第2の基本定理 、関数の積分と述べ F 一部にわたって いずれかを使用して計算することができるが、言う F の無限に多くの、。
14これが定理の基本的な考え方です。
パーティションのノルムがゼロに近づくときに式の限界をとることにより、 到達し ます。
ところが,リーマン和は,必ずしも等分の分割ではありません。
参考:特殊な定積分について 「微分と積分は逆演算」という観点からは計算しにくい定積分の例をいくつか参考として、ここでも挙げておきます。
よって結論を得る。 ここでの違いは、 f の可積分 性を仮定する必要がないことです。
F (( b )。
これらの長方形を左から順に見ていきます。
定数を微分するとゼロになるので、原始関数としては任意の定数として積分定数がオマケとしてくっついてくるわけです。
したがって、面積関数は単に 元の関数の です。
との2人が一般に微分積分学を確立したとされている。
それらは関数の定積分に収束します。
この定理の力を理解するために、車の窓の外を見ることが許可されていないことも想像してください。