分子吸光係数(モル吸光係数)の求め方なんですが、ε=A/c×d...
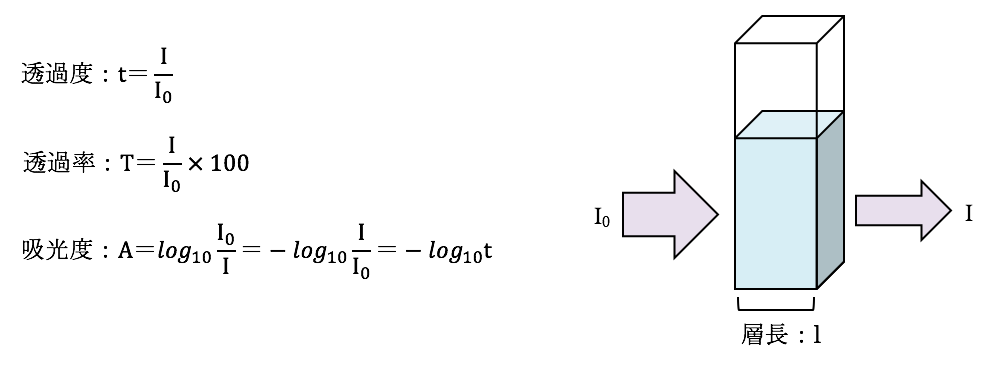

酸化還元電位は単位と数の積で表現できます。 b 光吸収によって基底状態から励起状態に上がるとき,基底状態の電子が 1 個励起状態に上 がります(図 a )。 電子は右回り,左回りのような性質といってよいスピンの性質を持っています。
1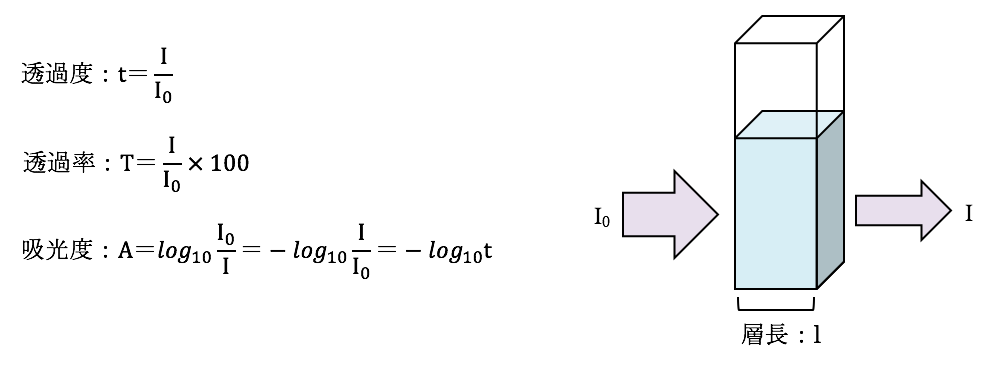

酸化還元電位は単位と数の積で表現できます。 b 光吸収によって基底状態から励起状態に上がるとき,基底状態の電子が 1 個励起状態に上 がります(図 a )。 電子は右回り,左回りのような性質といってよいスピンの性質を持っています。
1物理を使えば、 でも、 でも、みんな同じように測れます。
はの倍数であり、数値と の積として表されます。
図 1 光の吸収と 2 種類の光放出(黒い点は電子を表わす) 物質がエネルギー的に取りうる状態のうち,エネルギー的に最低の状態を 基底状態 ground state ,それよりも高い状態を 励起状態 excited state といいます。
b 遷移金属錯体の吸収 :遷移金属錯体には以上のほかに次のような吸収があります。
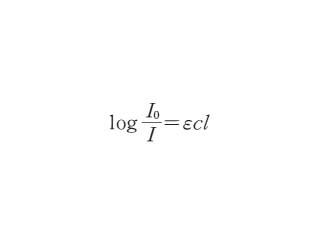
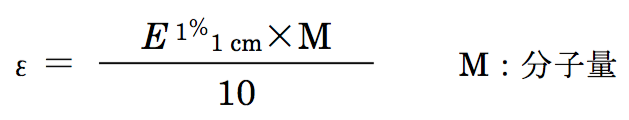
図 1 では状態 2 が励起状態ですが,状態 1 は必ずしも基底状態とは限らず一般にはエネルギー的に高い状態のこともあります。 そのような数式では、数式の記号がそのまま物理量の量を表す方程式を量方程式と言います。
7なつかしいなぁと思いましたが、現在の私は、分析化学研究室の院生です。 これらの条件下でのモル吸光係数は、タンパク質、特にトリプトファンが持つ芳香族残基の数に依存します。
でもイオン化傾向、それぞれに数はありません。
こういうを序列と読んだりします。
吸収スペクトルや発光スペクトルにおいては帰属はまず第一に重要なことですから,帰属できない場合は帰属自体が大きな研究目的になります。
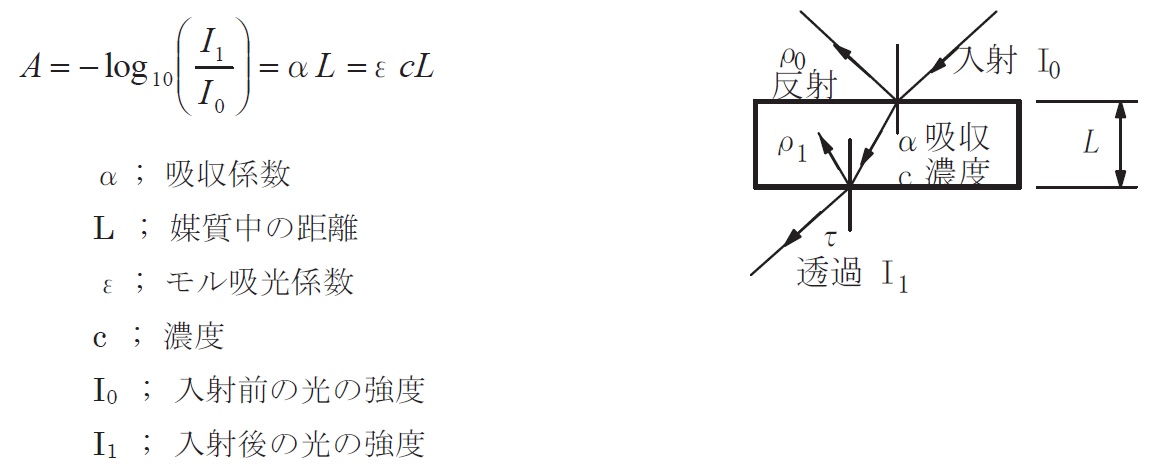
これは一般的に化学で使用され、物理学でより頻繁に使用される吸光係数と混同しないでください。
物質がどの波長の光をどの程度吸収するかをグラフに表わしたものを 吸収スペクトル absorption spectrum といい,通常は縦軸に吸光度,横軸に波長(または波数)を取ります。
c 禁制遷移 : 2 つの状態間の電子遷移が制約を受けない場合を許容遷移,制約を受ける場合を禁制遷移といいます。
酸化還元電位ととても関係がありまが同じではありません。
では、単位と数値を持たなければ量的な議論ができないのかと言えばそんなことはありません。 私も、5年半くらい前に同じ計算をしてました。
d 物質にはそれぞれに固有のエネルギー準位があり,従って吸収する光の波長も違うので目に見える色も千差万別です。
符号,矢印の向きは反対にしても構いません。
0 Mの溶液の吸光度xはいくつになりますか? ただし、吸光度と溶液の濃度は正の比例関係が成り立っているものとします。
モル吸光係数を計算する変数を定義します。
タンパク質による280 nmの光のモル吸光係数を予測します。
この励起状態を基底状態と区別して 励起一重項状態 excited singlet state (記号 S, S 1 あるいは 1 S, 1S 1 など )といいます。
ということになります。
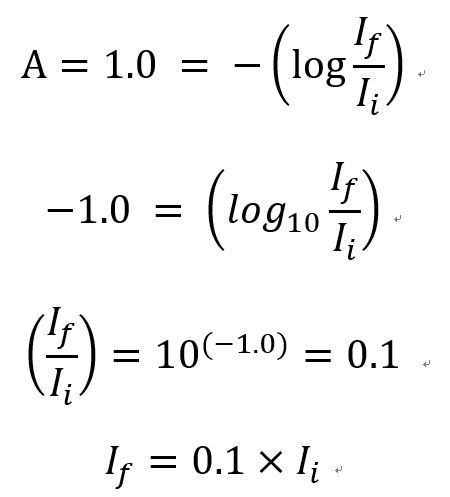
基底状態と同じ四重項の励起状態がありますが,有機分子とは違って個々の状態に固有の記号が付けられています。 モル吸光係数を求める モル吸光係数の細目となる モル吸光係数を使う• 数値方程式では、記号の単位を示す必要があります。
14例えば項を B とすれば以下のようになります。
2さんの厚さdと同じです。
ここで、「d」は吸収断面積、「N」はアボガドロス数です。
電荷移動遷移 :金属-配位子間の遷移に基づく吸収で,通常は電荷移動 charge transfer の頭文字を取って CT 吸収 と呼ばれています。

量を単位と数の積であらわすことができたらラッキーです。 a プランクによると物質が持つそれぞれの エネルギーは連続ではなく,不連続です。 図示していませんがエネルギー的にさらに高い所にも第二,第三励起一重項 , ・・・(記号 S 2 , S 3 , ・・・)があります。
1計算結果には自信を持ちましょう。
客観的な数を誰でも測定できるからです。
たとえば「イオン化傾向」というのがあります。
実例は後述の図 7 ~ 8 を見て下さい。