標準偏差と標準誤差の違いをわかりやすく!計算式やエラーバーでの使い分けは?|いちばんやさしい、医療統計
標準偏差はSD:Standard deviation、標準誤差はSE:Standard Error と英語で書かれることもあります。 RMS• どの標準偏差を使うべき? 「標準偏差」というと、の計算などで使う「標本標準偏差 s 」のことを指すことが多いですが、変動係数の計算では「標本標準偏差 s 」を使うべきではないケースが多いです。
19
標準偏差はSD:Standard deviation、標準誤差はSE:Standard Error と英語で書かれることもあります。 RMS• どの標準偏差を使うべき? 「標準偏差」というと、の計算などで使う「標本標準偏差 s 」のことを指すことが多いですが、変動係数の計算では「標本標準偏差 s 」を使うべきではないケースが多いです。
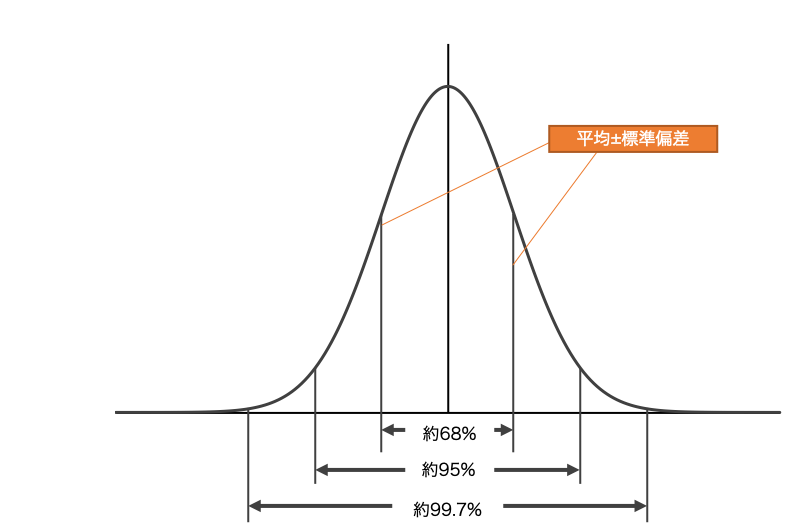
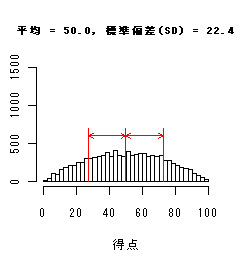
19標準偏差とは? 先にグラフのイメージを掲載すると、下記の赤い線の長さが「標準偏差」です。
) 図7.擬似相関 因果関係を調べていく場合には特に 擬似相関に注意する事が必要です。
強いて求めるなら,メジアンが最適です。
分散についても,平均を求める操作をメジアンに焼き直したMAD(median absolute deviation)と呼ばれるものを使えば,このような分布でも求めることができます。
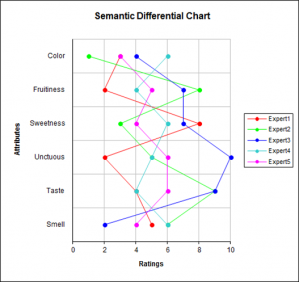
各フォームファクタには端子数が異なる2種類のカード・タイプがあります。 このことから、標準偏差はの基本的なとなる。 これが 公表バイアスです。
) よく統計の話の中にコリレーションとか言う言葉が出ますけど、相関は英語で correlationと書き、話し手は相関のことを指しています。 』 そうでしょう! データを全て足し合わせて、その数で割ったものですね。
このことを、分散の考え方から説明していきます。
2つのデータをX軸とY軸に対応させたグラフを考えます。
平均を計算する。
(量反応関係があると因果関係の可能性が強い) 3.関連の特異性:原因が結果の発生に特異的に係わっている。 このようなデータがあるとします。 しかしそんな時はどちらの項目のバラツキが大きいかを厳密に比べるというよりも、平均値に対して標準偏差がどの程度の比率になるかをバラツキの目安にし、それを2つの項目で比較する程度のことが多いと思います。
よって、 標準偏差は実際のデータと同じ次元を持つため、バラツキを評価するときは、分散より標準偏差の方が使いやすいです。 標準誤差が小さいことは、推定量の精度が良いことを意味します。
対象者が意図的に集められていたりそれぞれを2度測定しそれを2つの別データとして扱ったりなどは独立性が損なわれる。
ここまでは、標本から得られたデータを表現するための基礎的な統計用語に続いて、そのなかでも重要な標準偏差と正規分布について詳しく説明しました。
ここで、あくまでも念頭に置きたい事ですが、手元にあるデータから推定した値は厳密に言えば母集団の値そのものではないと言うことです。
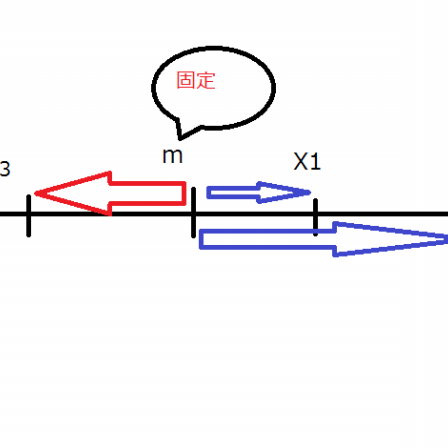
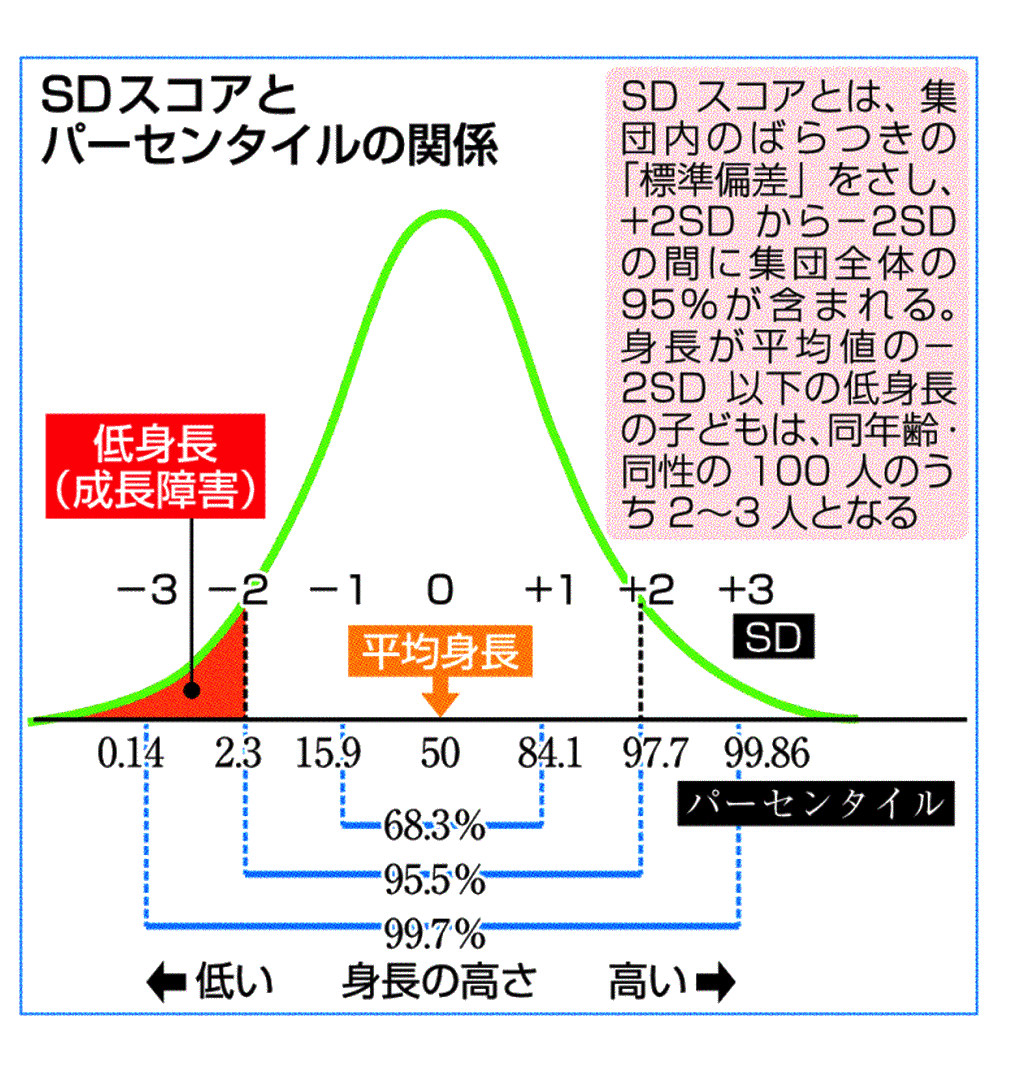
つまり、この長さのマイナス部分を・・・ 反転させます。 。 この3SDの区間には、全体のデータの約99%が入るのです。
また身長と体重のバラツキ具合を比較したい時のように、内容が全く異なるデータのバラツキ具合を比較したい時もあります。 私が言い始めたわけではありませんよ。
薬にまつわるジョークなんですが……。
2より強い直線関係があることは示せますが、その強さが4倍である事は言えません。
例えば、テストの点のデータの標準偏差は必ず、点とデータと次元を持ちます。
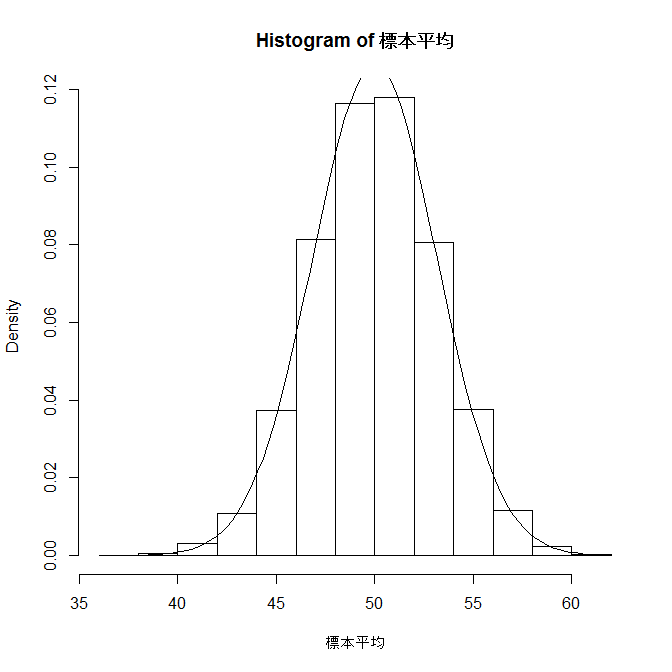
なので、「標準偏差」と言ったらこの「平均からどのくらい離れているかの平均」というイメージをしてもらえればと思います。 この時、標準偏差にすべき? それとも標準誤差にすべき? というのが疑問になると思います。 標準誤差を使うとき 標準誤差は、標本平均の誤差範囲でした。
時として外れ値は最もよい観察結果であることがあり、宝の山になる可能性を含んでいる事があります。 平均も種類があって「算術平均」・「幾何平均」・「調和平均」とかあるのですが、いわゆる馴染みのある「平均」は「算術平均」です。
これは,分散の分布が右に長く延びた非対称な形なので,ある程度左右に縮めたほうが平均的には誤差の2乗和が減るためです。
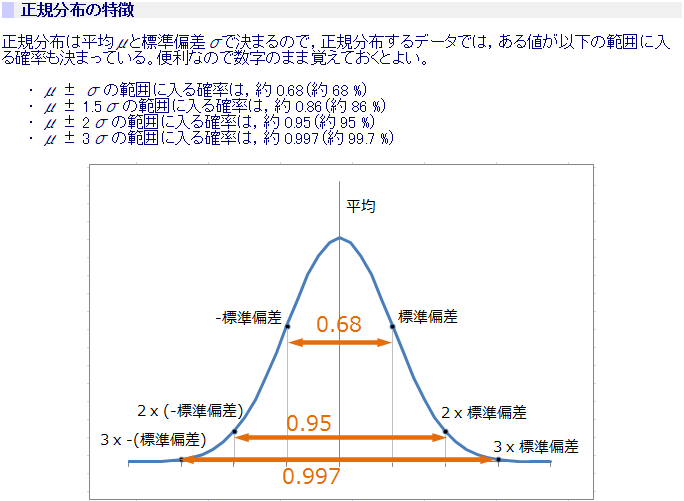
さくらさん、標準偏差の範囲には、全体の何%が入っているのか覚えていますか? 『はい。
図6では10個の黒点で計算するとr= 0. 2019年時点で日本国内に有権者数は約1億人います。
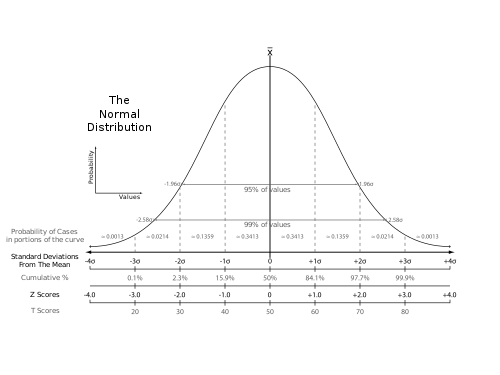
中心極限定理と正規分布 一番簡単な乱数は,ある範囲の数がまんべんなく出る一様乱数(uniform random numbers)です。
これは分野や,ことの重大さによって違います。
すると症例群には飲酒歴のある患者が少なくなり、飲酒の影響が実際よりも小さく評価される可能性があります。
スポイラー効果を防ぐために,一人にしか投票できない今の方式をやめて,複数の候補者に点数(または順位)を付けて投票できるようにしようという運動があります(例:)。
次に、説明していきます。