カイ二乗検定。カイ二乗検定のわかりやすいまとめ

【医療関係者のための統計解説】カイ2乗（χ 2）検定の使い方とは？｜薬剤師の悩みを解決するサイト｜HitouchMedi

$検定カイ二乗$

逆に言えば、セットの割合が同じであれば、比較することができると言えます。

この記事では、JMPにすでに用意されているサンプルデータを使います。

例えば薬剤群で治った人のカテゴリに関する期待度数。

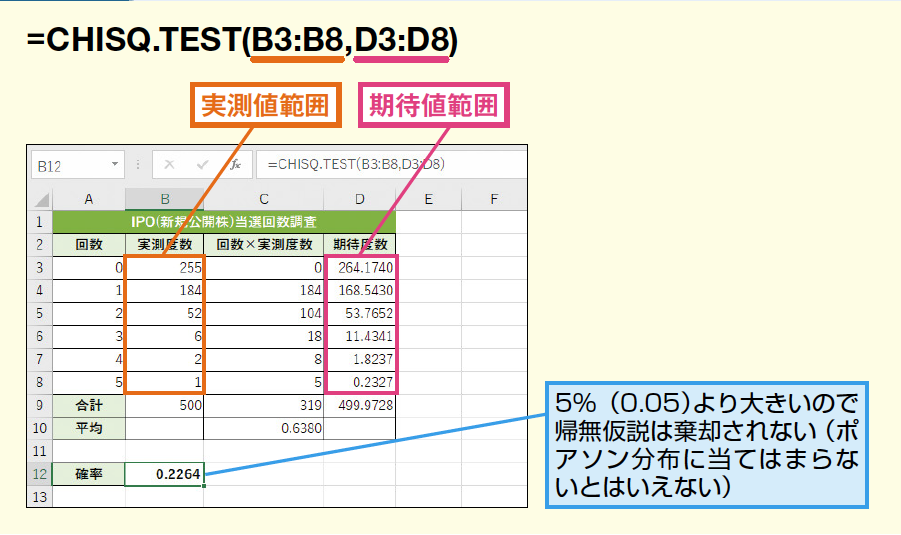
有意差がなければ学会発表・論文投稿できない• この計算式をもとに各カテゴリで計算すると、以下のような表を作ることができます。

今回はP値：3. これを期待値と言います。

カイ二乗検定・適合度検定の計算法を例題から解説。確率の偏りに惑わされないための統計的検定とは｜アタリマエ！

また、冷却パットを当てたときの体表面の温度を計測した場合の経時的変化は、フェルミ関数をフィットすることで階段的変化を係数として表すことができる。

カイ二乗検定: 適合度の検定 by Excel 内容が増えてきたので、以下の 2 項目はのページに移動しました。

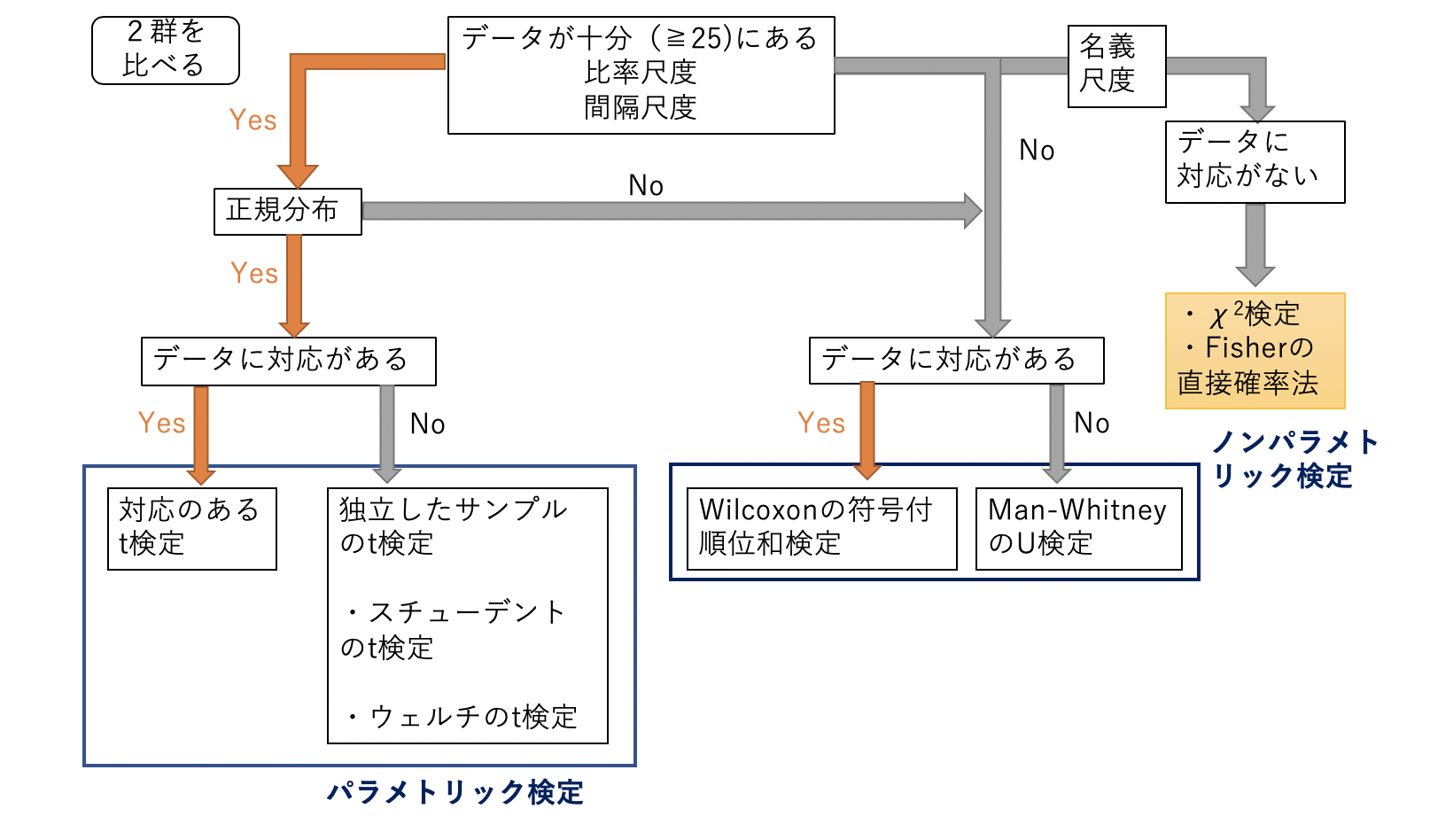
これらはパラメトリック検定を参照と呼ばれる検定方法で計算されます。

カイ二乗値を計算。

詳しくは、をご覧ください。

エクセルではCHISQ. dist x, 自由度, 関数形式で、x はカイ二乗値、自由度は自由度、関数形式は TRUE なら累積密度関数、FALSE なら確率密度関数である。

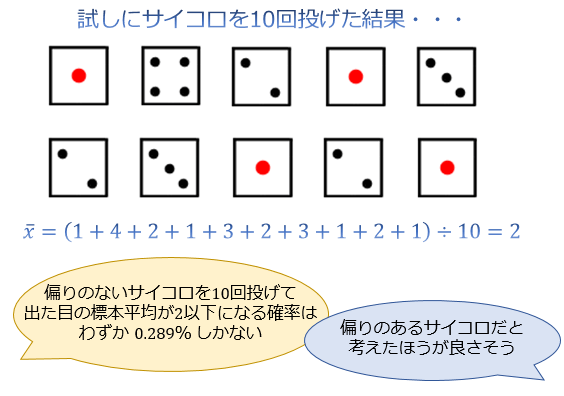
。有意水準は、本来示したい仮説と逆の条件（帰無仮説）の下で起こりうる確率なので、確率としてはかなり低いはずです。

コントロール群で治った人のカテゴリ• カイ二乗検定の結果は期待値と実際の値の間の有意性を表す。

Rでカイ二乗検定の実践をしたい方は参考にどうぞ。

EZRもRと同様に完全に無料であるため、統計解析を実施する誰もが実践できるソフトになっています。

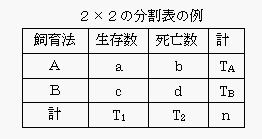
治った治らなかった薬剤群 1. 全標本数が小さい場合は、、さらに2x2分割表で表される場合にはを用いる必要がある。

Data Format ドロップダウンリストから適切なデータフォーマットを選択します。

期待値Eが小さい（標本数が小さい、または観測数が少ない）場合は、二項分布を正規分布ではうまく近似できないため、この場合にはの1つであるを用いるのがより適切である。

次のようなものを含む。

カイ二乗検定の結果を残差分析独立性のカイ二乗検定を行ない、二つの変数の関連が言えたとします。

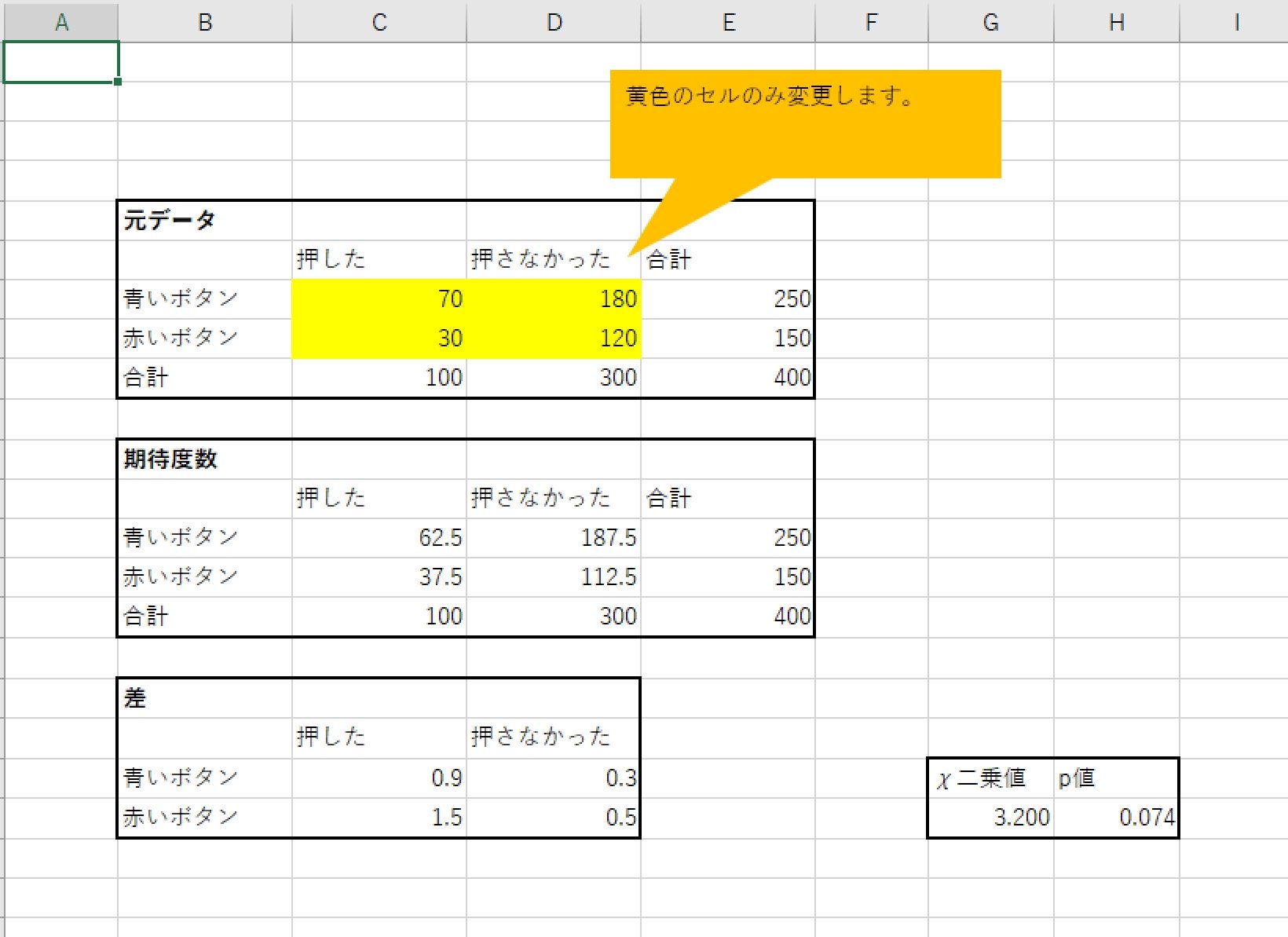
05を下回るので、独立ではない。（これは、観測度数と期待度数の差の二乗を期待度数で割った値の和で計算される。独立性の検定は、二つの変数に関連が言えるのか否かを判断するためのものです。

二つのパターンでキャンペーンをして結果を比べますが、集計しただけで結論を出していたかもしれません。

フィッシャーの直接法 Fisher Exact Test では、観測した特定の 2 x 2 分割表の両側確率を正確に計算しますので、全てのセルの期待度数が５を上回る必要はありません。

他からの束縛や支配を受けないで、自分の意志で行動すること。

手順３. T検定は各データ群の「平均の差」を比べます。

カイ二乗検定とは？カイ二乗検定とは帰無仮説が正しいとしたもとで、検定統計量が（近似的に）に従うような手法の総称です。

950006097 という値になるはずである。

もっと具体的に言うとこの表をクロス集計と言いますが、クロス集計されたデータにはカイ二乗検定を使うのです。

ワークシートの行と列は、それぞれ群とカテゴリに対応します。

言い換えると「2つの変数が独立している」ということ。