wmf.washingtonmonthly.com:いまさら聞けないIT用語集 浮動小数点演算の単精度と倍精度って? (1/3)

ここから次のことが導かれる。


ここから次のことが導かれる。
100000023841858 1つの精度値を正確な倍精度値で乗算した結果は、2つの単一精度値を乗算した場合とほとんど悪くありません。 421875」の部分の小数部を、23ビットの2進数にした物である。
単精度浮動小数点型と倍精度浮動小数点数型、それぞれ値がとりうる範囲を教えてください。
この例では、2つの値が両方とも等しく、等しくないことを示しています。
以下に幾つかの 32 bit の浮動小数点数のビットパターンを示します。
MSXの場合 [ ] MSX-BASICの演算ルーチンMATHPACKの場合、同様に4バイトで表すが、IEEE 754とは異なり• 丸め誤差との違い 丸め誤差: 10進数から2進数に変換する際などに特定の桁数で四捨五入や切捨てなどを行うことで生じる誤差。 たとえば利息の計算。 基本情報技術者」 翔泳社• 50000 0111 Inf NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 1000 -0. 2進小数の主な利点は高速性とメモリ消費にあり、BCD小数の主な利点は現実の10進小数を誤差なく扱える事にあったと言ってよい。
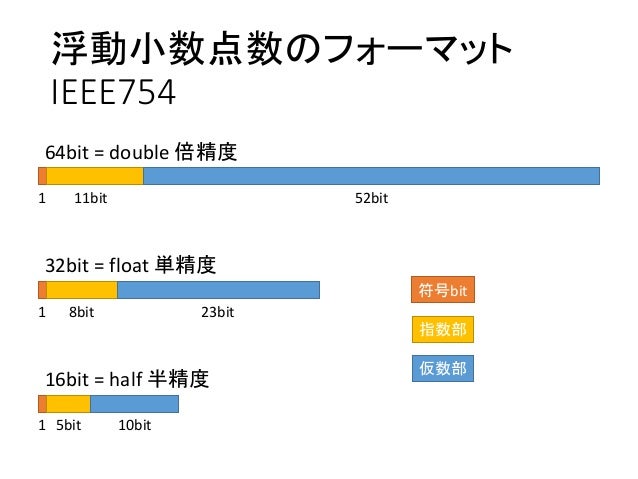
14IEEE754の表現形式 IEEE754標準は32ビットの単精度浮動小数点数(単精度とは32ビットのこと。
「アルファベット1文字+数字」で記載することができるので、デバイスコメントの文字数制限を圧迫することもありません。
単精度の数値は、実数の概数を格納します。
DF ' パソコンIFデバイスに、最大温度を格納 '------------------------------------------ ' 最小温度を求める D00445. ラダープログラムの演算命令では、扱うデータ型をアルファベット1文字で表現することが一般的なので、そのアルファベットに使用する、というものです。
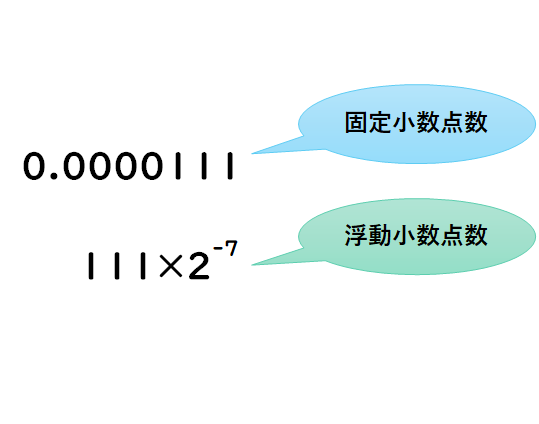
例えば全体を1000倍したら「1000に加算できるのは0. 123 を IEEE 754 binary32 フォーマットで表す場合を考えてみよう。 ほとんどのでは標準の組み込み型として定義されている。
Framework の型。
つまり32桁)を次のように表現する。
すべてのワークロードで高精度が要求されるわけではないため、AI や HPC の研究者は異なる精度を組み合わせることでメリットを得ることができます。
設問 1 次の単精度表現が表す数値として正しい答えを,解答群の中から選べ。
浮動小数点数の加減算は指数部を大きい方に揃えてから仮数部同士の計算をするため、数値の差が大きいと小さい値は指数を大きくするために仮数部が0になってしまうからです。
実験コード 符号部、指数部、仮数部を指定して単精度浮動小数点 binary32 のビットパターンを生成して値を確認します。
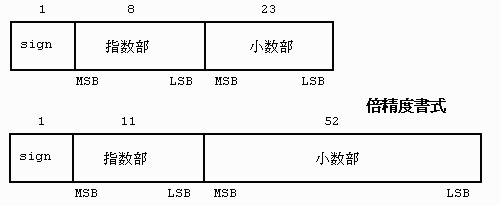
もくじ• floatのフォーマットはIEEE754という規格で 符号部:1bit 指数部:8bit 仮数部:23bit と定められています。
この領域での演算過程で0. 組を構成する要素の数がひとつ減ったのは、 指数を示すビット列が全て 0 になったときだけが、 非正規化数の出番だからです。
DF ' パソコンIFデバイスに、最小温度を格納 '------------------------------------------ ' 平均温度を求める D00412. 上記の様に、正負を示す符号と指数を用いて数値を表現します。
地球科学• 価格を抑えてゲームもできるモバイルノートPCがほしい人は要チェック• 一方、 記憶空間の問題を例にとれば、 倍精度浮動小数点形式をとるデータは 単精度浮動小数点形式をとるデータの倍の記憶空間を必要とします。
doubleの仮数部は52bitあります。

これは対数は桁数を表すという概念からきています。 符号部は、変数で表現できないからでしょう(たぶん)。 簡単な例で言うと、 円周率は3. ここも前回と同じですが、非常に大切なので、再度ご紹介します。
20仮想アクセラレーター プログラムのメンバーである 社 本社:米国サンフランシスコ は、NVIDIA V100 Tensor コア GPU の混合精度コンピューティングを利用して、医療事務を自動化するディープラーニング アルゴリズムのトレーニングを高速化しています。
昔のFORTRAN言語では,整数型と実数型は同じ語長を占めることを前提に言語の規格が制定されていたりもした。
923桁分で、つまり有効数字が7桁にならない。
2進小数の主な利点は高速性とメモリ消費にあり、BCD小数の主な利点は現実の10進小数を誤差なく扱える事にあったと言ってよい。
場合によっては、共通言語ランタイムで Single 変数を緊密にパックし、メモリ消費を節約できる可能性があります。 0000001192092895507812500000000000000000000000 1. いまやあらゆるプログラムで浮動小数点数が使われていますが、ここで改めてその性質を確認してみましょう。 ただし当時のスペックにおいて10進小数は相応に重い処理であり、DAAという10進補正用の専用CPU命令を持っていたZ80であっても複雑な演算になればなるほど 例えば三角関数や対数関数のような数学関数 2進小数より負荷が増していく。
17この時点ではまだ浮動小数点の表記になっていません。 詳細はに関する開発者リソースを参照してください。
ほとんどの場合、"be" が等しい数になるほどの違いがあります。
ピックアップ• 00000011920928955078125が限界」、つまり 1. IEEE754の場合、指数が2 -126よりも小さいとオーバーフローとなります。
コンピューター サイエンスではこれを精度と呼び、通常は 10 進数ではなくビット、つまり 2 進数を単位とします。