万有引力是怎样产生的?


卡文迪许认为,铜球没有磁力,所以测的是万有引力而不是磁力。 在这个扭曲的时空中,传统的欧几里德几何学几乎毫无用处,他需要用全新的思维方式和全新的数学工具来解决扭曲时空的问题。 同样地,未来人类在对更加广阔空间的探索中,必然会发现更多相对论无法解释的现象。
15

卡文迪许认为,铜球没有磁力,所以测的是万有引力而不是磁力。 在这个扭曲的时空中,传统的欧几里德几何学几乎毫无用处,他需要用全新的思维方式和全新的数学工具来解决扭曲时空的问题。 同样地,未来人类在对更加广阔空间的探索中,必然会发现更多相对论无法解释的现象。
15但是在弱引力场的情况(例如太阳系)下,对许多力学问题,用牛顿万有引力定律比用爱因斯坦的广义相对论计算要简单得多,而且两者相差极微。
牛顿的万有引力定律是天体力学的基础。
第一步:设有两个质心间距离为r的物体,质量分别是M1和M2。
万有引力存在的实验证明和引力常数 G的测定是卡文迪什于1798年作出的。
第二步:用g1表示M2相对M1自由落体运动的重力加速度,用g2表示M1相对M2的重力加速度。
光子逃离引力场时发生光谱红移 2018年5月,欧洲南方天文台的科学家们将望远镜对准了距离我们2. 牛顿是伟大的。 同时还需要在3~5个方向上照相记录,所以,仪器附有,并安放在特制的小房里工作。
在这个决定的过程中根本就不需要万有引力的参与。
其中G是牛顿引力常数。
我们从万有引力和球表面积成反比可以看出,万有引力就是磁力,英国科学家亨利• 互不平行或弯曲时,两个重荷将受到水平分量的作用。


爱因斯坦也知道两个物体之间的引力与它们的质量成正比,所以他说物体的质量决定了能量-动量密度,能量-动量密度造成时空曲率,并且与时空曲率成正比,进而确定了引力场的强度。 因此,牛顿万有引力公式6. 305米)木棒的两边并用金属线悬吊起来。 根据1684年8月~10月的《论回转物体的运动》一文手稿中,牛顿很可能在这个手稿中第一次提出向心力及其定义。
6卡文迪许用铜球作的扭秤实验测的不是万有引力其实是磁力。
牛顿自己说: 我还没有能力去从现象中发现产生这些重力特性的原因,而且我无法臆测……我所解释的定律和丰富的运动的计算已经足够于说明重力的确存在并能产生效果。
二者应该分开对待。
至少,在万有引力计算公式中,M与m之间应该是相加而不是相乘的关系。
在质量M磁场中的m所受到的力必然和质量M的磁感应强度B1M和m的质量成正比为B1Mm。 利用万有引力公式,开普勒第三定律等还可以计算太阳、地球等无法直接测量的天体的质量。
扭秤实验:18世纪末,英国科学家亨利• 虽然的假设的确比牛顿的假设更能精确地解释确定案例中万有引力的作用效果,但是他也从来没有在他的理论中为这种能力赋予一个原因。
就像两辆汽车在交通事故中相撞,精确地计算出冲击力的大小并不能证明肇事者是谁一样。
在质量m磁场中的M所受到的力必然和质量m的磁感应强度B2m和M的质量成正比为B2Mm。
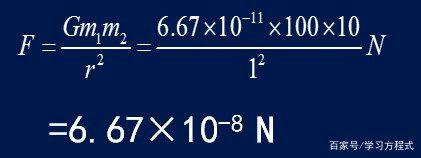

在天体中质量还算很小的地球,对其他的物体的万有引力已经具有巨大的影响,它把人类、大气和所有地面物体束缚在地球上,它使月球和人造地球卫星绕地球旋转而不离去。 由此可知,这两个力与两个天体质量的乘积成正比,它称为万有引力。 关于万有引力究竟是一种什么力,牛顿和世界上的科学家们谁也没说清楚。
5他将小金属球系在长为6英尺(1英尺等于0. That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it. 严格地说,上式是对两质点而言的。
牛顿用万有引力定律证明了、月球绕地球的运动、潮汐的成因和地球两极较扁等自然现象。
他认为物体在引力场的运动是沿四维弯曲的黎曼空间的短程线。
因此如何激发学生求知欲,培养学生学习物理的兴趣,是提高教学质量的关键。
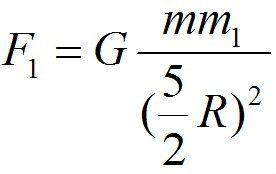

万有引力公式中的质量M与m为何是相乘而不是相加的关系呢?牛顿没说。 有很多高中生,是非常想知道,高中物理万有引力公式有哪些,小编整理了相关信息,希望会对大家有所帮助! 万有引力公式都有什么 1. 其中G代表引力常量,其值约为6. 如果一个是质点,另一个是有限体,则可把有限体分割成许多质点,并求出它们引力的矢量和,就能得到整个有限体对质点的作用力。
15牛顿的普适的万有引力定律表示如下:任意两个质点有通过连心线方向上的力相互吸引。
我们知道磁感应强度与球表面积成反比,也就是球表面积越大磁感应强度越小。
地球膨裂说认为,引力大小与它们质量的乘积成正比这可以理解,引力大小与它们的距离成反比也可以理解,可为什么引力大小与它们距离的平方成反比呢?牛顿没说。
就这么简单。
四维时空则可能不是平直的——它可能是以球面为代表的正曲率空间,也可能是以马鞍面为代表的负曲率空间,只有在曲率为零时它简化为平直空间。 万有引力公式(关于引力,爱因斯坦是对的) 引力是什么? 这是几百年来许多科学家苦苦思索的问题。
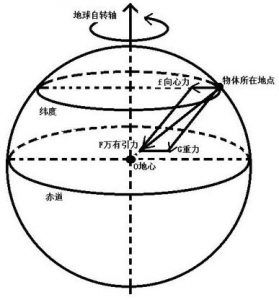
10万有引力应用范围 通常两个物体之间的万有引力极其微小,我们察觉不到它,可以不予考虑。 爱因斯坦以加速坐标系和引力场的等效性否定了惯性坐标系在宇宙空间的存在,又用引力场改变了空间特性。
天文学家还曾预言黑洞的存在,使广义相对论进入了与宇宙演化有关的新境界。
直到今天,我们依然在利用万有引力定律来解决身边的许多力学问题,一方面在许多物理场合我们用不着那么精确,另一方面因为万有引力定律简单且优雅。
伽利略在1632年实际上已经提出离心力和向心力的初步想法。
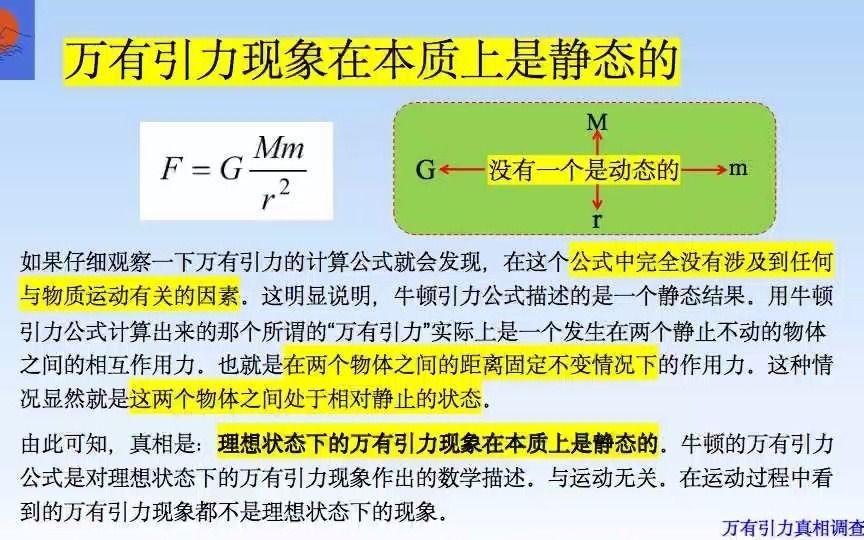
物体的质量越大,它们之间的万有引力就越大;物体之间的距离越远,它们之间的万有引力就越小。 因此,英国科学家亨利• 为什么?本人给出的答案很简单:牛顿对万有引力的定性是错的。
7例如:怎样才能简单推导这个公式? 而用相对论解释:万有引力其实是不存在的,它不过是时空扭曲现象的必然结果而已。
所有以上的预言有些已经通过观测与实验得到了验证,有些部分得到了验证,所有的这些都是万有引力理论所力不能及的。
但是,如果理论上出现了错误,尽管计算结果是正确的,但在解释问题的时候也会遇到麻烦。
人造卫星、月球和行星探测器的轨道,都是以这个定律为基础来计算的。
作者:赖柏林. 如果把它投影到三维空间中,恰好是行星在太阳引力作用下的椭圆轨道。 为英国科学家 卡文迪许通过扭秤实验测得。
,式中 G称为。
水星轨道进动: 1859年,法国天文学家勒威耶在利用牛顿万有引力定律计算水星轨道时发现存在误差,他发现水星在其轨道近日点的实际观测进动值比理论计算值每100年快了38角秒。
而万有引力其实就是物质存在的一种信息场。