2次元回転行列の導出

何故最初がz軸なのかと言いますと、一番2次元の座標変換の説明と結びつけやすいからです。


何故最初がz軸なのかと言いますと、一番2次元の座標変換の説明と結びつけやすいからです。
当たり前といえば、当たり前ですが。
Isoclinic decomposition 4次元の回転を左 isoclinic 回転と右 isoclinic 回転に分解する.• この場合は、座標系A X-Y が移動してできた座標系A' X'-Y' の存在は薄いかもしれません。
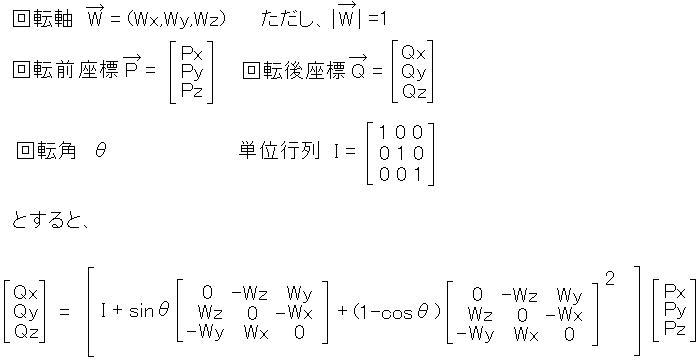
2次元の R で考えると、 となります 長さ=1は自乗した形で比較。
3次元の座標変換も2次元の座標変換と意味合いは同じで、同じ点をそれぞれの座標のなかで表したら、何処になるのかを求めることです。
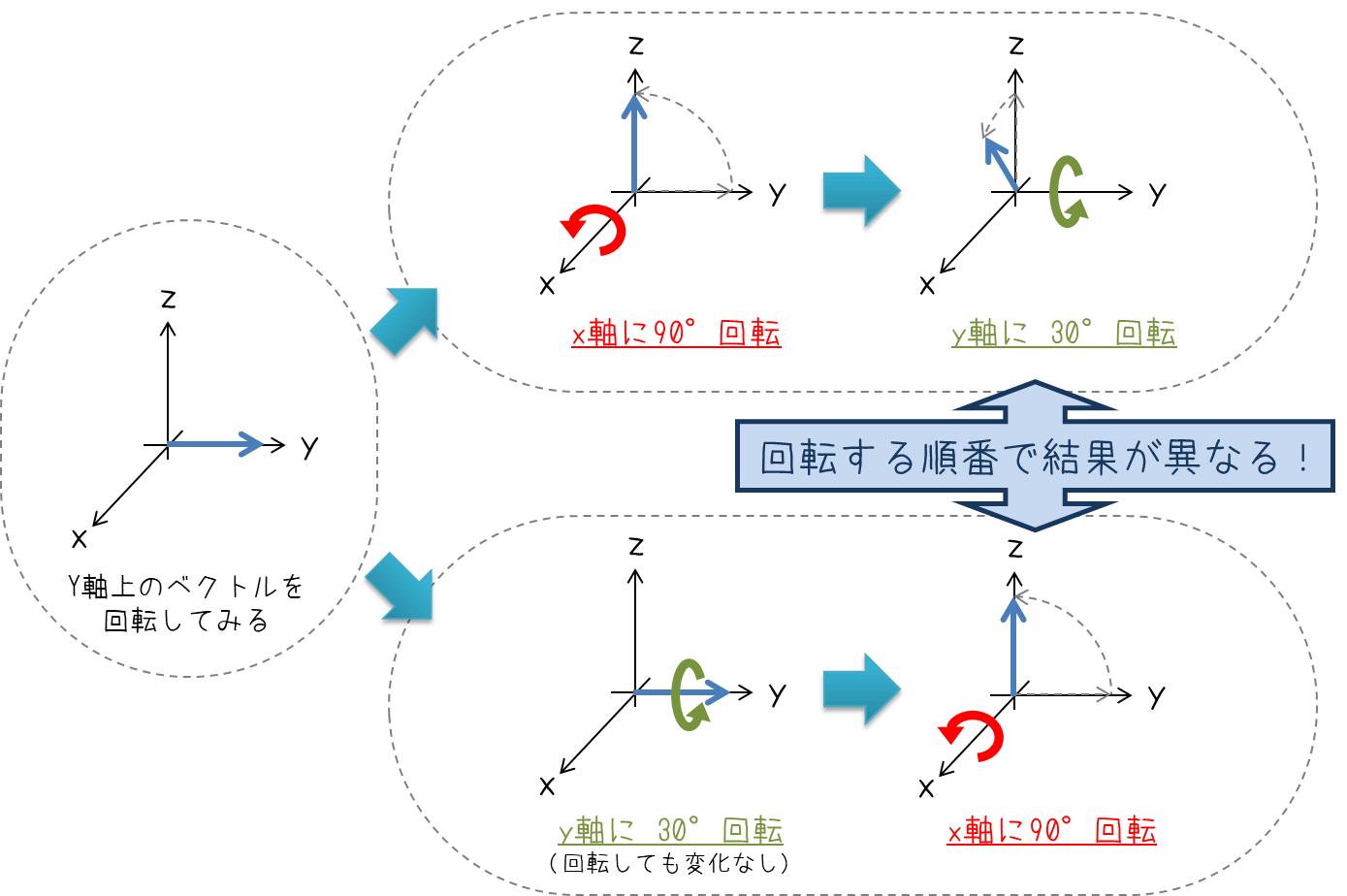

基本原則として、これらの変換には順番があります。 自分のなかでもごちゃごちゃにするとたいへんですので注意しましょう。 そこまでは屁理屈をこねず 笑 、床に固定したら動かないと考えることにしましょう。
16図の面内での回転をそのまま3次元的に見て、Z軸まわりの回転と考えます。 そのような部分や分かりにくい点、曖昧な点を指摘してもらえると、とてもありがたいです。
簡単ですね。
以下の例では、Z・Y・X軸回りに順に回転させています。
簡単なので、座標変換の意味をちょっと考えてみます。

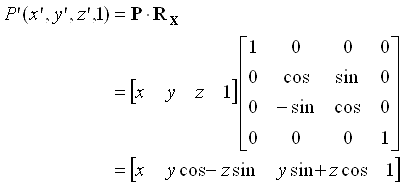
同次変換のご利益=変換の連続 座標系を3つ、A,B,C を考えます。 プログラム実行結果 ラベル、視点などは手動で編集しました 2-2-2. ちなみに、先に平行移動してから回転させることももちろん可能ですが、この図と同じ角度、移動量のままで順番だけかえると違う結果になることはわかると思います。 平行移動や回転移動などの移動 全ての点の座標は下のようなベクトルで表します。
ある点と点の相対的位置関係を表すベクトル 相対ベクトル は、当然ながらかわりません。 この関係は座標軸AとBでどちらが主ということはありません。
おそらく覚える必要はないと思いますが、一度は求めておくと納得しやすいのではと思います。
さて、「 R で回転、 q で移動」という手順を逆変換するには、「 q だけ戻す、 R で逆回転」という手順になります。
回転の場合、直感的に分かりにくいこともあるため、実際に数字を入れてみることが肝心です。
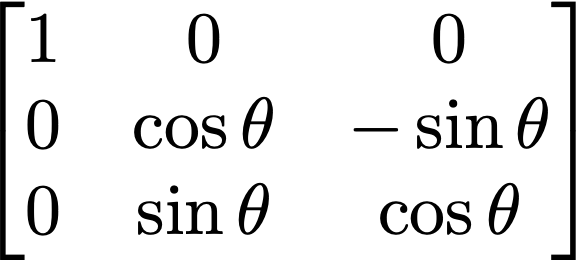
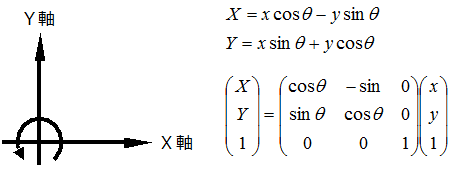
本文中の文字も数式にすると行間などがひどいことになるので、ご了承下さい。 おわりに すこし図解も言葉も足りなかったかと反省していますが、とりあえず回転の座標変換の説明を書き上げました。 3次元の回転方向は,右手系では回転に対して右ネジの進む方向で表します. これはベクトルなので, スカラーである 内積では表せないことは明らかです.• 合同な場合に限るのは、一つには話が簡単になるからですが、ロボット工学という分野を考えた場合、物体の運動や関節の角度変化などでは、ものそのものの大きさは変わらず、それに固定された座標系も形を変えないためです。
17平行投影• 計算誤差が少ない.• これは、「合同な変換のみを扱うこと」にしたことに起因します。 」と思いますが、他の全ての移動が掛け算で出来ているので、足し算を実装するのが綺麗では無いからこのようにしているのだと思います。
計算は先ほどと殆ど同じですね。
[Z],:本記事の図はTeX TikZ でつくりました.• [C]:本記事で解説する「行列は単位ベクトルの変換先を並べたものである」という性質から,行列表示(行列表現)が理解できます.• あとは、座標系の移動にともなってその座標に乗っていたものがどう移動するか、あるいは、ある座標系上のものが別の座標系からどう見えるか、について確認しましょう。
ただ、導入動画の最後に出てきた通り、弱点として「ジンバルロック」という現象があります。
これは途中でX軸回りに180度回転させたことで、同じZ軸回りの回転が逆回転になること、さらにこの過程でY,Z軸の方向も逆になることに起因します。
平行移動 平行移動は非常に簡単です。
二次元座標 X,Y座標 の場合のアフィン変換行列については で説明しましたが、今回は三次元座標 X,Y,Z座標 のアフィン変換となります。
だいたいはこのパターンが成り立つと思いますので、覚えておくと一種類覚えておけば残りも導けますので便利です。

車両の走行経路に障害物がある場合、それを検知してよける必要があります。 そのため、両者の関係を入れ替えると、 になります 入れ替えたとき、角度も逆向きにすることに注意。 • なお、本によって回転順序が異なったり、回転軸をZ0,Y0,X0にとっていたり、いくつか種類があることに注意が必要です。
13ある軸周りといったときには、正の向きを決めておかないと2方向があるからです。
2次元の場合でみて、 ですが、そもそもの導出の前提、 と見比べると、 R の第1列目が u の x 成分と y 成分そのものを表していることがわかります。
これで、座標系そのものの移動ができます。
このとき、2次元と同じように、 と書くことができます。
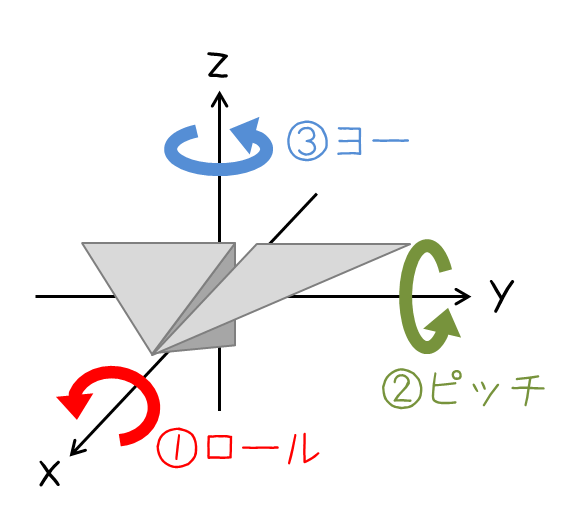
以上、長かったですが、ロボット工学に必要な、座標変換について終わらせました。 上と下は重力に対して定義し、上下軸に直交する1本の軸を前後軸として定義する。 高速.• このため、本ブログでは表記を使い分けつつ、必要に応じてベクトルを行列とみなして演算する、といった方法で解説しています。
20この見え方は2次元のxy座標を回転するときの見え方と全く同じです。 大半の応用で扱うのは2次元や3次元の回転だが、一般の次元でも回転行列を定義することができる。
4次元の物体を画面に描画するまでを考える• おそらく、いままで、平行移動といった場合に、たびたび出てきて、ぱっと思い当たるのは右の図の 1 だとおもいます。
これをそのまま3次元に拡大すると、「原点を通る軸を中心に回転」となり、特に扱いの容易な座標軸を中心とした回転を考えます。
変換行列に三角関数を ルールに沿って 含めることで、大きさを保ったまま、向きだけを変えることができます。

注意点として、あるベクトルに回転行列を適用する場合は、上記の通り必ず「左から掛ける」事です。
つまり、 q だけ移動してから R 回転した場合は、別の変換になってしまいます。 この表現はマイクロソフトがお得意で、DirectX(Direct3D)や. 左辺は極座標基底での成分表示になっています。
この場合、S軸はZ軸そのままになります。
つまり、 と、同次変換についても、逆変換は逆行列で行えることが確認できました。
2次元ベクトルの回転行列 まずは簡単に考えるため低い次元で考えます。