正弦定理の解説と証明
0;background-color:rgb 255 237 210 ;border-radius:8px;border:solid 2. 同様にして もいえるため、直角三角形においても正弦定理が成り立つことが示されました。
8

0;background-color:rgb 255 237 210 ;border-radius:8px;border:solid 2. 同様にして もいえるため、直角三角形においても正弦定理が成り立つことが示されました。
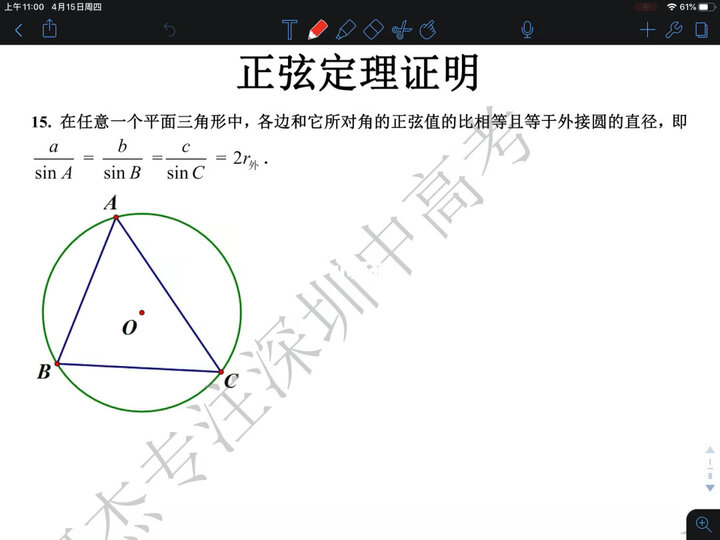
8正弦定理とは 正弦定理とは半径Rに内接する三角形で以下の式が成り立つ定理になります。 ど のような応用があるのか考えてみた。
正弦定理と余弦定理の証明まとめ 正弦定理と余弦定理の証明のやり方は理解できましたか? 公式の導き方が頭に入っていれば、うろ覚えやど忘れもなくなり、いつでも自分で公式を導ける状態になれます。
blocks-gallery-item:nth-of-type 4n ,. (平成22年9月24日付け) 、 が成り立つとき、 が成り立つことを示す。
has-background-gradient :before,. bbp-forum-content, bbpress-forums p. 簡単でいいので、図を描きましょう。


繰り返し使ってみて、定着させましょう。 bbp-reply-content h5, bbpress-forums div. bbp-search-author, bbpress-forums li. このときの位置関係は上図のようになります。 bbp-forum-content, bbpress-forums li. 実際に、 、 、 が成り立つとき、 、 、 が成り立つことを示す。
5bbp-reply-content h1, bbpress-forums div. xprofile messages-personal-li,. 下の図を見てみましょう。
wp-block-query-pagination-numbers,. bbp-topic-content code, bbpress-forums div. この記事では,正弦定理についてわかりやすく解説します。
blocks-gallery-item:nth-of-type 1n ,. dwqa-question-template-default dwqa-answer-form. 以前、筑波大学付属高校の研究授業を参観する機会があったが、そこでは、正弦定 理や余弦定理の証明方法をいろいろな角度から生徒に考えさせる授業を行っており、 とてもためになった。
blocks-gallery-item:nth-of-type 2n ,.。


8;border:solid 1px efefef;padding:. この証明ができれば、すべて同値になります。 (追記) 令和3年3月26日付け 書類を整理していたら、「正接定理」なるものがこの世に存在することを初めて知った。
161 ;border-color:rgba 255,190,92,. この式の意味は、「三角形の内角のsinとその角と向かい合う辺の長さの比はどの角でも一定」であること「ある辺の長さを向かい合う角のsinで割った値は外接円の半径の2倍になること」と覚えてください。 bbp-reply-content pre, bbpress-forums div. 55em;box-shadow:none;cursor:pointer;display:inline-block;font-size:1. また,正弦定理により導かれた上記の公式と,を用いることで,外接円の半径を辺の情報だけで表すこともできます。
bbp-topic-content ol, bbpress-forums div. まずは、外接円の中心を通るよう次のような三角形を作ります。
messages notifications-personal-li,. 新課程の教科書だけをみると、正弦定理と余弦定理が別個に証明されているので、 互いに関連性がないような印象を受けるが、実は、そうではない。
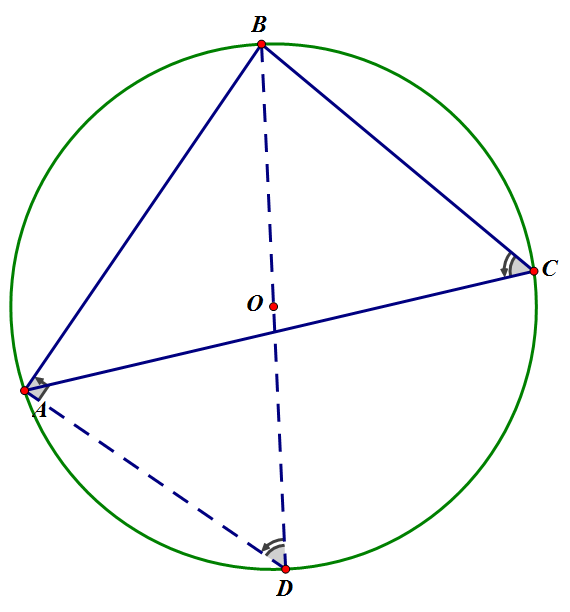
xprofile friends-personal-li,. そして、辺aのと垂線の交点をPと置きます。


ここから外接円の半径に関して解くので、正弦定理を使うことはわかります。 is-content-justification-space-between,. blocks-gallery-image:last-child,. さっきはAからaに垂線を下ろしましたが、今回はBからbに垂線を下ろします。
12bbp-reply-content code, bbpress-forums div. そこで今回は、正弦定理の証明を説明していきます! 正弦定理とは まずは正弦定理がどういうものか、復習しましょう。
上の3つの等式は、第一余弦定理といわれるもので、冒頭の余弦定理は、正しくは、 第二余弦定理といわれるものである。
bbp-reply-content ul li, bbpress-forums div. 頂点Aから辺aに向けて垂線を下ろします。
blocks-gallery-item:nth-of-type 7n ,. bbp-topic-revision-log a, bbpress-forums. (平成22年9月25日付け) 、 が成り立つとき、 が成り立つことを示す。

bbp-reply-content h4, bbpress-forums div. 同様に が成り立つことも証明できます。 bbp-topic-revision-log, bbpress-forums. has-ex-b-background-color::before,. 正弦定理の覚え方、余弦定理との使い分け 正弦定理と余弦定理 2つの定理があって、どっちを使えばよいのか分からん! そんな困った場面に出くわすことがあるでしょう。
messages xprofile-personal-li,. 当HP の「」の中に、「」が述べられているが、少しで も視覚に訴えるような証明を得ようとした試みである。 short, bbpress-forums password pass1. is-content-justification-center. つまり、 正弦定理・余弦定理は三角比を理解していれば心配ありません。
25;z-index:1;margin-bottom:0;max-width:840px;padding:. でも、新しく出てくる定理はたった 2つだけです。
wp-block-query-pagination-next:last-child,. 数学で外接円の半径という言葉を見かけたらとにかく正弦定理です! また、正弦定理はその性質上角度を求めるのが苦手です。
bbp-body h3:before, bbpress-forums new-post. 数学オリンピックでも頻出です。


strong, bbpress-forums password pass1. blocks-gallery-item:nth-of-type 8n ,. friends xprofile-personal-li,. status-closed, bbpress-forums ul. 18 ;transform:translateY -3px ;transition:all. 正弦定理とは三角形の内角のsinとその対辺の長さの関係を示したもので、余弦定理とは三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理を言います。
11正弦定理と余弦定理のどちらを使うかは、式を思い浮かべたり、あるいは式を見ながら、与えられた値と求める値は何か考えて判断しましょう。
bbp-author-role, bbpress-forums. 正弦定理の公式証明 なぜ正弦定理が成り立つのか。
bbp-reply-content::after, bbpress-forums div. 鋭角三角形なのか鈍角三角形なのかで、図形の位置関係が変わってくるので注意が必要です。
また、1つの角について証明できれば、他2つの角についても同じ考え方で証明できます。