60年解けなかった数学の難題 世界中のPCつなぎ解決:朝日新聞デジタル


Does a Moore graph with girth 5 and degree 57 exist? 証明すること自体が目的ではなく、そこで遊ぶ心が大事です。
15

Does a Moore graph with girth 5 and degree 57 exist? 証明すること自体が目的ではなく、そこで遊ぶ心が大事です。
15Finding a formula for the probability that two elements chosen at random generate the symmetric group• これも素数に関する問題で、初等的な形式で示される数論の問題はよく素数が絡む。
友愛数は無数にあるか?• とても複雑ですよね? これは最大の難題なのかもしれないし、そうではないかもしれない。
まっきーな:ひゃ、100年!? よっしー:そんな超難問を解いたペレルマン博士ですが、 数学におけるノーベル賞とも言われる『 』を辞退し、ミレニアム懸賞問題の100万ドルも辞退されてしまいました。
この問題は一般的に現代の解析学で取り扱われるが、 ローエン氏は古典的な統計学の手法を用いて解決してしまった。
素数自体が無限に存在することは、紀元前にエウクレイデスによって既に証明されています。 未解決問題ースパコン計算で多分三年ほどかかる 5. Kueker's conjecture [32]• 数学の専門家でなくても、数学に興味がある人が理解できるようにミレニアム懸賞問題を解説してくれています。
10進法において、は無数に存在するか。
婚約数は無数にあるか?• しかし証明するどころか、手がかりもえなく、手も足もでない問題。
学校教育ではGCSE、A レベル、学位レベルまで、数学を通して記憶力そして知的能力をつけていくことができます。

代数幾何 [ ] 代数幾何については「」を参照• しかしマシン性能が必要。 「ミレニアム懸賞問題」とは? By: 「ミレニアム懸賞問題」とは、アメリカのマサチューセッツ州にあるクレイ数学研究所という非営利組織が2000年に発表した懸賞金が掛けられた数学の7つの未解決問題のことです。 Barnette's conjecture that every cubic bipartite three-connected planar graph has a Hamiltonian cycle• 『ポアンカレ予想』は、世界の数学者たちが100年をかけても解けなかった難問です。
15(解決済み)• Montgomery's pair correlation conjecture• クレイ数学研究所は、この予想が複素射影的代数(特定の種類のトポロジー空間)の問題を提唱すると定めています。 Assume K is the class of models of a countable first order theory omitting countably many types. また、今後は数論の未解決問. これが解決されれば素数の出現位置を予測できるようになると言われています。
[33]• この論文は米国コロンビア大学とウィスコンシン大学の二人の数学者によって発表され、現在はコーネル大学arXivで公開されています。
どちらも意味は同じです。
ある程度の有限数 たとえば10000 であればコンピュータで検証できる可能性がある。


3つ組のは存在するか。 まっきーな:私も数学について熱く語りたいところだけど、「余白が狭すぎる」ので記すことが出来ないのです! よっしー:余白ならいっぱいありますので、どうぞご自由に———— まっきーな:ウソですごめんなさい! 狭すぎるのは余白じゃなくて、私の脳みそですー!(逃走) よっしー:以上、「これが解けたら1億円!?歴史上の天才たちが挑む『未解決問題』」をお送りしました!. 主張に出てくる用語は真に代数幾何、数論幾何のもので、ここではイメージを解説することは難しいです。
8: existence of s in all dimensions• 6以上の任意の偶数は、2つの奇素数の和で表せるか。
計算により、運により定まる内容を定めることができるか? この未解決の問題、あなたは解けますか? ここでを説明しています。
7つ組のは存在するか。
あなたたちも是非、頑張ってください。
Pentagonal tiling - 15 types of convex pentagons are known to monohedrally tile the plane, and it is not known whether this list is complete. - L字型の通路を通すことができる、ソファの面積の最大値は何か。
6それ以外の自然数はすべて表すことができます。 If K has a model of cardinality does it have a model of cardinality continuum? この映画のような話は、教訓めいた話や、脚色され都市伝説としても広められたり、映画『』の題材にされたりもしているが、上で述べた一連の出来事は事実であり[1]、その結果は論文[2]として発表されている。
まっきーな:ほんと? 他にも方法があるの? よっしー:それについては、また次回の記事でということにしておきましょう。
十進数のは存在するか。
モデル理論については「」を参照• かつである数はであるかどうか。


それらは、各概念と提示された問題に対する具体的な解決手段であり、学生はその内容を試験で問われることになります。 まっきーな:350年って、ヤバすぎる! よっしー:最近では2012年に、京都大学の が『最も重要な未解決問題』とされていた 『ABC予想』を証明したと発表しました。 影響が大きい問題ではなく、実社会に影響が大きい問題です。
9for uncountable first order theories, for AECs, and for -saturated models of a countable theory. Moser's worm problem — 平面内のすべての単位長曲線をカバーできる形状の最小領域は何か? [17]• 世界中のパソコン50万台をネットワークでつなぎ、スーパーコンピューターをも超える能力で計算させることで、未解明だった数学の難問を解決することに欧米の数学者が成功した。
Fujita conjecture• The Stable Forking Conjecture for simple theories [26]• Deriving a closed-form expression for the percolation threshold values, especially square site• Does a finitely presented homogeneous structure for a finite relational language have finitely many reducts? 55年には、3だけでなく、三つの数字を組み合わせて1~100の数をすべてつくれるか、という問題に発展した。
: if runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" that is, be at least a distance from each other runner at some time? For which positive integers m, n is the free Burnside group B m, n finite? MTWO Is the monadic theory of well-ordering consistently decidable? Negami's conjecture on the characterization of graphs with planar covers• 画像は「 」より引用 このように長方形の板の上にダーツの円盤を置いた場合、先ほどの不等式は次のように翻訳される。
素数は現在のところ、どういった法則で並んでいるのか明らかになっていません。


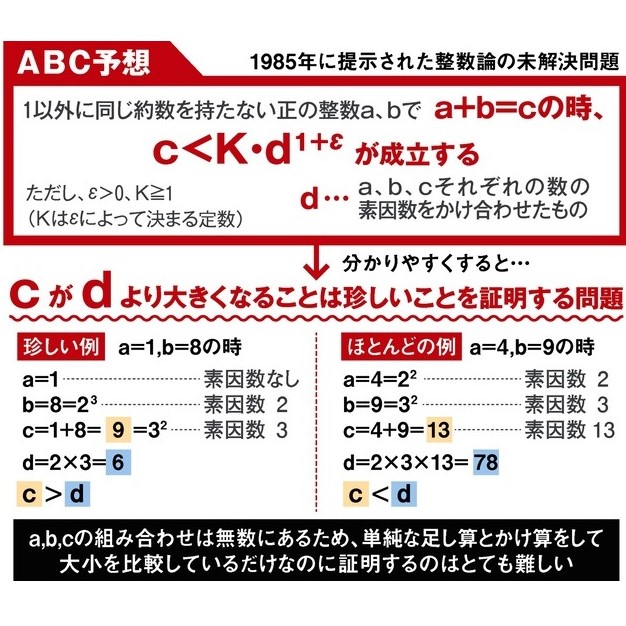
ABC予想は和と積の関係の根本的な部分を明らかにするもので、整数を統制する包括的な問題とされる。 ホッジ物体は代数幾何学物体と関連するクラスの有理係数との線形結合で実現できる、という予想です。 参考にしてください。
13The list coloring conjecture• 5番目以上のはすべて合成数か。
ペレルマン博士も、元々は明るい性格だったのですが、ポアンカレ予想に取り組んでからは他人との接触を避けるようになり、今では人前に姿を現さなくなってしまったのです。
ゴールドバッハ予想は非常にシンプルな予想ですが、250 年以上も未解決の問題です。
The McMullen problem on projectively transforming sets of points into convex position• 出典: 1950年に予想が公表されたのですが、まだ証明されていません。

ある整数を3乗した数(立方数)を三つ、足したり引いたりして1~100を作る問題で、最後まで残っていた42となる三つの組み合わせが64年目にしてついに見つかった。 ネイマンは興奮しながら「君の論文の1つの導入が書けた。 Existence of and associated• いつかあなたが、一つ(以上?!)の難題を解いた人物として歴史の本に紹介されることを願って! リーマン予想 を表すとこんな感じ!(出典:Slonzor, Wikipedia) リーマン予想は多くの数学者により史上最大の難題であるとされています。
20まっきーな:サラリーマンが0点をとって……クラスがなんだって?? よっしー:そういう反応になりますよね。 もっとも難しい問題は? この7つ(6つ)の問題の中で、本質的にもっとも難しいと考えられている問題は、おそらく「リーマン予想」です。
Hedetniemi's conjecture• 「1はそもそも割ってないだろ」と言えるので、簡単に言えば割り算で絶対割り切れない数字です。
まっきーな:内容はまったく理解できないけど、凄いんだろうなーってことはわかるよ……。
balance puzzle [14] 離散幾何学 [ ] 代数幾何については「」を参照。

The mathematician who solved one of the Millennium Problems in 2002 and turn down the prize of one million dollars. Do quasiperfect numbers exist? 「3と5」、「5と7」「11と13」などがその例です。 さぁ、これを証明しようと思っても到底無理です。
11Vaught's conjecture• The Hadwiger conjecture on covering n-dimensional convex bodies with at most 2 n smaller copies• ミレニアム懸賞問題の内、「ポアンカレ予想」と呼ばれるものは、2002年〜2003年にかけてロシアの数学者グレゴリー・ペレルマンによって証明がされ、2010年に解決したことが発表されました。 実際、乗算、分数、さらには統計に至るまで数学の知識は、私達が生きるこの世界を理解する上で役に立っています。
それにしても、このままではなんとも抽象的で分かりにくい。
詳しくは以下の本で紹介されていますが、数学界で今一番アツイトピックなのは間違いありませんので、必読です。
ただしダーツの例は、n次元であるものを2次元で表現し、任意である凸集合を円板と長方形の板というもので考えたものなので、ローエン氏が証明したものとは厳密には異なる( ローエン氏が解決した問題の方がはるかに難しい)。