ファン・デル・ワールスの状態方程式

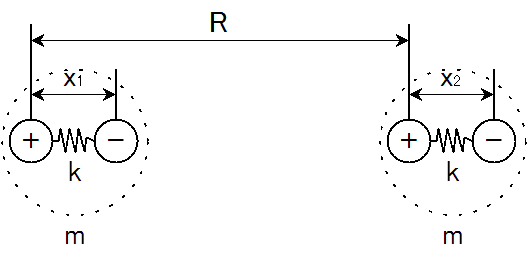
飽和蒸気圧曲線の近傍に於いて液体側からその飽和蒸気圧曲線に近づく s 液 p,T 曲面と、気体側から飽和蒸気圧曲線に近づく s 気 p,T 曲面が、蒸気圧曲線の所で連続的に繋がっている訳ではありませんので、その位置における完全微分条件を、そこでの議論のように用いるのは正しくありません。 状態式ともいう。 理想気体 現実には存在しない理想的な気体。

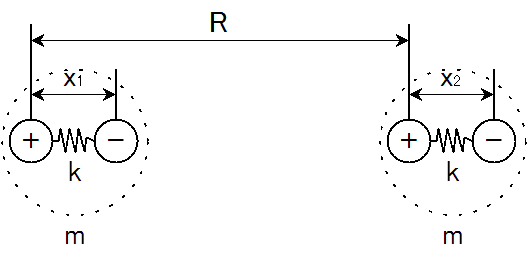
飽和蒸気圧曲線の近傍に於いて液体側からその飽和蒸気圧曲線に近づく s 液 p,T 曲面と、気体側から飽和蒸気圧曲線に近づく s 気 p,T 曲面が、蒸気圧曲線の所で連続的に繋がっている訳ではありませんので、その位置における完全微分条件を、そこでの議論のように用いるのは正しくありません。 状態式ともいう。 理想気体 現実には存在しない理想的な気体。
熱源が飽和蒸気のみの伝導伝熱式での乾燥方式でありながら、外気をなるべく取り入れない他にはない独自の機構で乾燥機内の温度は、外気温度に影響されず常に高温で一定に保たれています。 極性がない分子を無極性分子、極性がある分子を極性分子。
これはかなり難しい教科書ですが、ゾンマーフェルトの説明の仕方や言い回しの端々に、熱力学や統計力学が作り上げられていった時代の状況・雰囲気を伺うことができる。
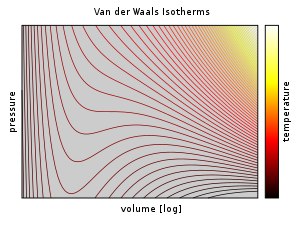
図4.点 A より右側は気体の領域を、点 E より左側は液体の領域を表わす。
このときの補正圧力は理想気体の状態方程式中にどのように組み込まれるであろうか。

内管の B には試料を入れたガラス小球を置いておく。
より正確に, 圧力に寄与する量とは 単位面積・単位時間あたりに粒子群が壁面と衝突する回数であった. 感謝!• この概略を図示すると右図のようになります。
このとき、 q 転 は(p,T)の関数です。
そのため、 気体が示す圧力は、理想気体の方が実在気体よりも大きくなります。
さて, 分子間力が存在する立場では分子どうしが互いに引き合う引力によって壁面に衝突する勢いと頻度が低下することが予想される. 水が凍るときには膨張するので、仕事をさせることができる。
どちらも分子間力によって減少する。
うまく描けましたか。
また、二つのパラメータだけで理想気体からのずれを表現しているため、のように系統的に近似の精度を上げていく事が出来ない欠点もある。
ファン・デル・ワールス気体について、幾つか参照しました。
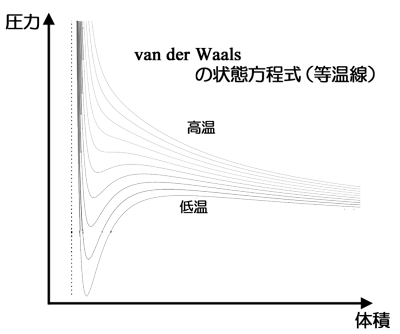
熱力学的な立場からファン・デル・ワールスの状態方程式を導出するときには気体の 定性的な振る舞いを頼りにすることになる. 分子が動き回れるのは、内容積から分子自身の体積を引いた部分だけになるのです。 密度が十分に小さい希薄な気体ほどあるいは高温および低圧になればなるほど理想気体に近い挙動を示すようになります。
参考:• 正確に言えば,物質の三態によらず存在し得ない。 これは気体の種類によらない普遍的な式となる。
分子間力 分子間同士で働く力。
内管の C を操作し,ガラス小球を落下させて割ると試料は蒸発し,その蒸気が内管中の空気を追い出すのでガスビュレットの液面が下がる。
1 分子自身の体積 理想気体では、分子自身の体積を0と仮定していると説明しました。
これについてはマクスウェルの等面積則という、ありがたいルールがあります。 分子間に働く力が無視できる. 内部の気体がどういう性質かは、全く関係なく決まりました。
これなら二次方程式です。
この中の二酸化炭素の三態の状態図は となる。
ここで単位には注意です。
このとき 他の物理量は、飽和蒸気圧曲線の真上の部分で、気体側から伸びる状態量曲面と液体側から伸びる状態量曲面は互いに交差することなくすれ違いで反対側の領域にのびていることに注意してください。 つまり、実用温度で測った各転移温度に於ける転移熱と相変化に伴う体積変化を用いることにより、その実用温度tが絶対温度Tで何度になるかが決定できるのです。
vii となります。
どこもできない付着物、粘着物が乾燥できる は、日本 2件、海外7ケ国 9件の特許を取得済み独自技術を持つ画期的な乾燥装置です。
、 は気体によって異なり、それぞれの気体で固有の値となる。


また、 高温になることによって、分子の運動が高速になり、分子間力(ファンデルワールス力)が無視出来るようになるからである。 日本語で読めるものは、わずかにMax. ここからは、飛ばしてしまった曲線 ABCDE の意味を補足していきますが、細かい話なので理解できなくてもかまいません。
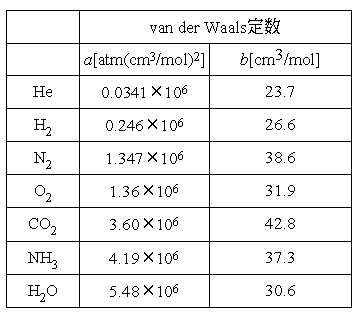
5係数 a,b は実在気体の理想気体からのずれを表現するパラメータで気体の種類ごとに定まり、 ファン・デル・ワールス定数と呼ばれる。 次図は表のaとbの値を用いて描いた T=270Kにおける 二酸化炭素のp-v線図です。
しかし、とにかく上記の様な関係を導くときに一定値となる示強性の状態量である。
これが導出の手順です。
一方,T<T cであれば, 1 は2つの解をもちその解の間にひとつの変曲点を持ちます。


つまり理想気体と同じように 定積比熱は温度だけの関数である。 単位もない数値で聞いてくるなんて、この分野の学習や仕事をしている人とは思えませんが、ちょっと暇になったので、考えて見ましょう。
3ファンデルワールス力 電荷を持たない中性の分子間にも弱い引力が働いており、化学結合していない分子間や原子間にも互いに引きつけあう相互作用。
また、単に交わるのではなくて、接触するようにして交差する場合を 二次の相転移と言います。
実際に窒素の値を使って計算し、それをグラフに合わせてみましょう。
このファンデルワールスの状態方程式により蒸気の性質が理解できます。