埼玉県公立高校入試問題 2021。 2021年度埼玉県公立高校入試過去問【数学】解説

【高校受験2021】埼玉県公立高入試＜社会＞講評…定番な問題が多かった

今週末は、いよいよ高校入試本番です。数学に苦手意識の強い受験生にとっては、かなりの鬼門になったのではないでしょうか？とはいえ、学校選択問題を受験校に選ぶ受験生にとっては、情報を的確に整理する思考力は必須です。このほかの教科（全5教科）についても同様に掲載する。

福島県関東・甲信越• また英作文問題の指定について、学力検査問題では「文の数」ですが、学校選択問題では「単語数」になり、より様々な文法や熟語を使う必要が出てきます。

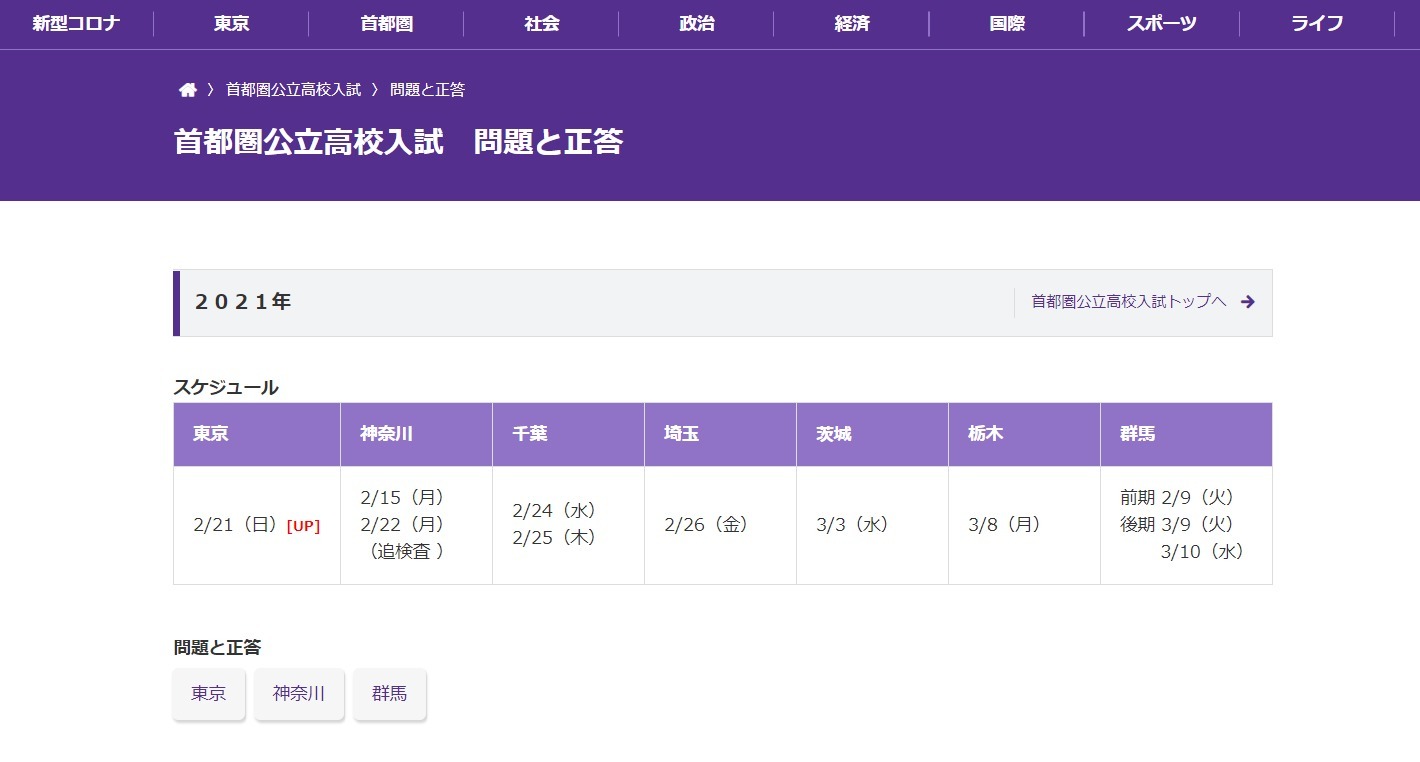
また、以下の進路希望状況調査にあるように、県内公立の志望者が減少する一方、県内私立の志望者が増加しています。
正答率は選択問題：60〜70％、並び替え問題：43％、英文を書く問題：10〜20％となっています。
【社会】：学力検査問題・小問数の減少。

2021年度埼玉県公立高校入試解答・解説理科（2021年2月26日実施）│Future Earth〜ミライの地球を考える〜

大変な時期を乗り越えての受験時期でしたね。使用する英単語は基本的なものですが、綴りや使い方に落とし穴があるため、しっかりと対策しておきたいところ。リスニングは満点だった、という皆さんも多いのではないでしょうか。

英語全体の出題傾向それでは入試当日、最後に行われる科目である「英語」を見ていきましょう。

・学年別の問題構成比として、２年生時の範囲が増加傾向となりました。
すべての受験生にとって、それぞれが納得できる結果であってほしいと思います。
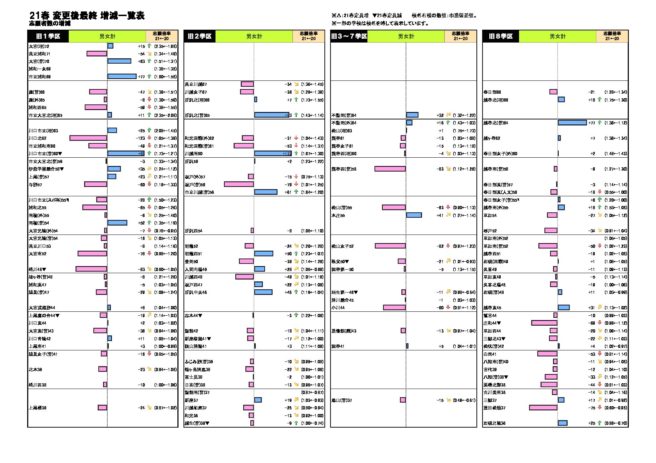
2021年度入学者選抜は、全日制が募集人員3万6,280人に対して3万9,157人が受検し、うち3万4,681人が合格（入学許可候補者）。

2021年度埼玉県公立高校入試過去問【数学】解説

英語は例年大問5つので構成されています。県北エリアだと、熊谷高校・熊谷女子高校・熊谷西高校で採用されています。

正答率は６０％程度となっています。

埼玉県公立高校入試に求められる英語力は他県と比較にならないほど高いものが求められるので、今後も要注意です。
岐阜県• 合格した生徒には、その喜びを常に忘れてほしくないと思いますし、不合格だった生徒には、その悔しさを常に忘れてほしくないと願っています。
受験生の皆さん、持てる力の全てを答案用紙にぶつけてきてください。

【高校受験2021】埼玉県公立高入試・学校選択問題＜数学＞講評…難易度ともに昨年同様

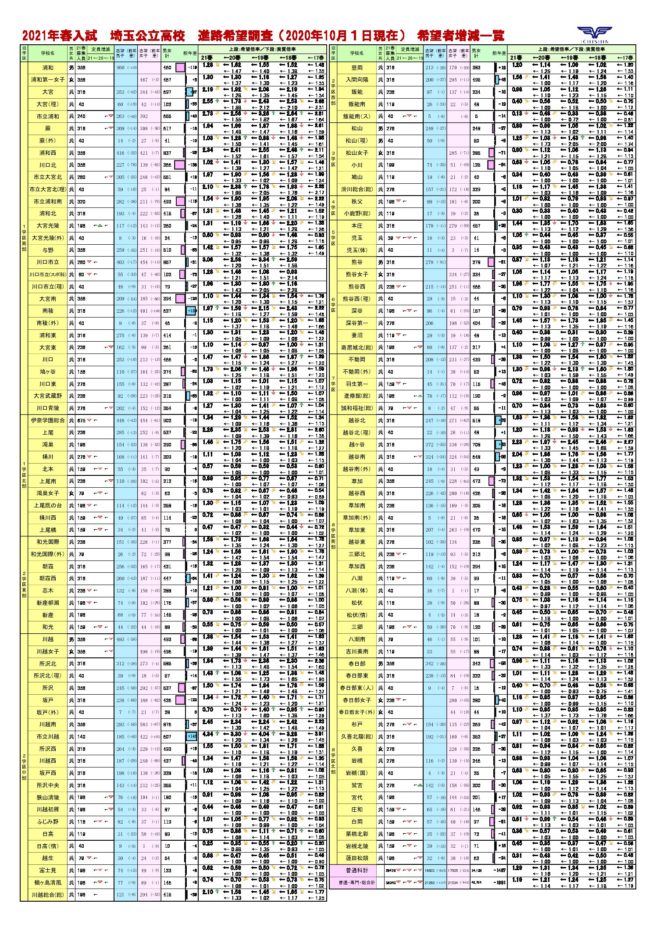
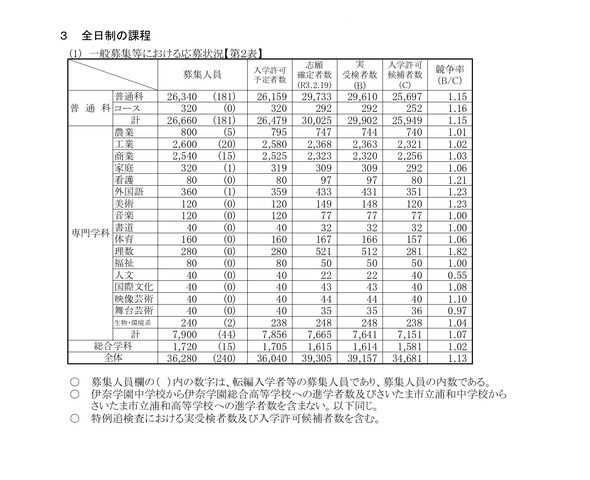
公立高校を第一優先に考える傾向が、今年度大きく変わってきたとも言える倍率ではないでしょうか？続いて出題された公立高校入試問題の学年別出題数です。図形の特性を正しく理解し、それを活用できるかどうかで差がついたと思われます。入試直前の今、ラストスパートをかけている受験生のために、各教科の傾向を考察してみたいと思います。

岡山県• 02倍だった。島根県• 説明も必要となるため、正答率が20％以下と難しくなっています。

二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。
計２０問。
リスニング令和2年度学力検査の配点：28点配点はここ数年変わらず28点です。

2021年度埼玉県公立高校入試解答・解説理科（2021年2月26日実施）│Future Earth〜ミライの地球を考える〜

全国北海道・東北• 1 では、相似の性質を用い、電柱の高さを求める問題でしたね。

ア・エのように、横に並ぶ場合は２個先が平行な面。最後の最後、何をやればいいのか。

上位高校を狙うのであれば、３年生時の応用単元を確実に演習することが必須であり、通常学力検査での高得点を奪取するためには、２年生時の苦手単元を確実に克服することが、志望校合格への最短距離になると言っても過言ではないと言えます。
佐賀県• 最も低い説明を伴う問題でも56％となっているため、学力検査問題を採用している高校で上位校（県北エリアでは本庄高校など）を目指す生徒は、ここは満点近くを狙いたいところです。
栃木県• また、不登校の生徒等を対象とした特別な選抜も実施され、405人受検したうち339人が合格した。