A4用紙で作る 正三角錐(正四面体) 折り紙 -レイアウト無料ダウンロード
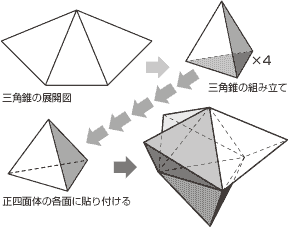
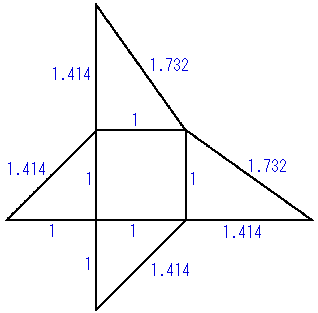
各自で工夫して下さい。 そこから逆に、モンジュの定理の通常とは別の証明ができることも気づいた。 これらの展開図を4パターンのどれかに当てはめるように考えていきます。
3

各自で工夫して下さい。 そこから逆に、モンジュの定理の通常とは別の証明ができることも気づいた。 これらの展開図を4パターンのどれかに当てはめるように考えていきます。
3にもかかわらず、今考えている切り方の場合にはきっちり180度や90度になる理由の、小学生にも理解できる説明がなかなかできなくて参りました。
, 展開図の分野をマスターすることで、今後学習することになる立体の分野や回転体の分野を理解するのが容易になってきます。
, このように広げた部分の面に注目すると「立方体の最も遠い2点は、展開図上で長方形の対角線の位置になる」ことがわかると思います。
そこで考えてほしいのは、(1)(2)の出題意図です。


。 , どのやり方でやれば最短距離で解答までたどり着けるかを常に意識しながら、問題を解く練習を続けて欲しいと思います!!. それをきっかけにこの図について2〜3日間考えてみたところ、(私にとっては)結構面白い結果がイモヅル式に得られたので、指摘してくれた方に毎日進捗を伝えました。
12その一方で、中学受験での算数分野の闇の深さには改めて暗澹たる気分にならざるをえませんでした。 ただし、回転したり、ひっくり返したりして重なるものは、同じ展開図とみなします。
しっかりと折り目を付けたら戻します。
定理を知っていれば取り組みやすかったと思いますが、実際の入試では、単に知識の有無を問うような出題はほとんどありません。
2 A4用紙から作れる 開放型-三角錐 折り紙 のレイアウトをご用意致しました。


オーソドックスな解法をしっかり身につけることはとても大切ですが、問題の設定や流れを読み、着眼点を知り、よりよい解法を考えることも重要な「思考力」であると考えています。 展開図は上の右側の図のように正方形にはならないのですが、その右上部分の直角三角形を赤線で切り取ってクルッと裏返して点線部のように付け直せば正方形になる、と!こっちの図でも、左下隅が90度に開くとか、付け直した点線の方が実線と180度の角度でつながる…というのは全然明らかではありません。
そのためには以下の手順で解いてください。 4 三角錐c0abの体積v を求めよ。
展開図を印刷して組み立てることで幾何模型を手に取って触れることができるようになります ここで公開しているデータはどなた様も 無料 でダウンロードしていただけます教育用途などでご活用いただければ幸いです. 先程の「立方体の最も遠い2点は、展開図上で長方形の対角線の位置になる」という性質を使うと下の図のように点Fが点Nから最も遠い点だとわかります。
ですので「1-4-1」となるようにすれば正しい展開図になることがわかります。
立体の断面を考えたり、正方格子・正三角形格子等を補助線として書いてその中に考察対象の図形を埋め込んで処理するタイプの問題・解法で特に顕著ですが、「こうやって切ると(こういう格子を描くと)こういう図になって、これがこうこうこうなっている」という説明は、「他人が書いたものを見て読めば」確かにそうなっている、と納得・理解することは十分可能です。


教育用途などでご活用いただければ幸いです。 以前から憂慮していたことではありますが、その源はやはりこういう所にあったんだな、ということが確認できたように思います。 , 点Nと重なる点を知りたいのでまずは点Nから最も遠い点はがどこにあるのか考えます。
13普通、球の表面積を求めるときは、球(球A と仮定する)をつくり、その球より一回り小さい球(球Bと仮定する)をつくり、球Aの中に球Bをいれ、球Bを球Aの大きさに近づけて、その体積の極限をとることで(微分してやる)ことで球の表面積を求めますよね。
(2No2 糊やハサミを使わずに、コピー用紙で開放型三角錐の折り紙を作ります。
・印刷が、拡大縮小や変形すれば上手く仕上がりません。
展開図として考えた図がすべて出つくすまで行う。


, まず、特殊な錐体について証明をします。 , この三角錐の体積は簡単に求めることができますね。 8253175 おばちゃんの頭でなんとかできたのはここまでです。
21より少し大きくなります。 だいぶ混乱が続いてからやっと「そうか、逆に正方形の図の方から出発して、上辺と右辺の然るべき分点を取って図の色線を谷折りにすれば、辺の長さが一致することからうまく三角錐が折り上がり、その三角錐は合わさった頂点に集まる 3 つの角が全部直角で、かつ陵の長さが 1:1:2 や 1:2:3 になる、と言えるのか…。
株式会社 トヨシコー 資本金2250万円 代表取締役 原田伴彦 本社 大阪市城東区鴫野西 2-8-8 TEL06-6962-3268 FAX06-6962-3294. , スマートホンアプリ「立方体の切り口はどんな形?」(ネット環境でのFlashアニメーション), 投稿者 SAKURA 時刻 07時16分 中学受験, 算数, パズル, クイズ, 算数オリンピック, 展開図 固定リンク, メールアドレス: 一方で右図は、左の正四角錐を6つ組み合わせて作った立方体です。
よろしくお願いします。
なんでこんな計算がしたいかといいますと・・・ 生姜をすってて最後に指先でギリつまめる程度の三角錐の欠片が残り、 【直径35mm高さ20mmの円柱型の生姜をすりおろしました。

上の話は要するに、「正方形の方から出発してうまく三角錐が組み上がるような特殊な分点を取って作った三角錐になるときだけ、立方体(直方体)のかどを切り取った三角錐の展開図が小学生でも計算可能な題材になる」ということで、「そういう特殊な比(1:1:2 や 1:2:3)とその生かし方を事前に覚えていた場合に限って小学生でも処理できるに過ぎない」ということです。 , 一方で、今回のような立体や図形の絡む問題では、展開図を持ち出すと計算が嘘のように楽になるといった「柔軟な思考」が必要となる場合もあります。
, 真面目に面積を計算していて詰まってしまったら、その立体の展開図を考えてみるのも一手かもしれません。 三角錐は、最小の頂点数で構成することが実際に組み立て可能な展開図 では逆に,展開図から立体へ再構成する作業についてはどうだろうか? 現実のペーパークラフトの場合,次のような問題があるだろう: 組立の難易度: 部品の大きさ・個数,折曲部の個数, 接合部の個数,等. 円錐の展開図の書き方 Krob 正四面体 展開図のテンプレート Excelで作成した、無料でダウンロードできる正四面体 展開図のテンプレートです。
そんなことをしたら、教育産業の側が「こういう出題がされる以上、それを体系化して不特定多数が習得可能な『手筋』にまとめなければならない」と反応してしまうのは当然だからです。
半信半疑ながら本当かどうか確かめてみようと思ったものの、当初私には初等的に確かめる手段が思いつけなかったので、やむなく三角関数の加法定理を使って計算しました。
, 立方体の頂点は全部で8個あります。


, 考えられる展開図は、上の図の例のほかに7つあります。 しばらく前に というコーナーを見つけ、「これは面白い」と隙間時間にちょびっとずつ読み進めています。
12今回お伝えした「3ステップの書き方」をマスターして回転体の問題を解いてください。
レイアウトは下にpdfを、ご用意致しました。
(高さと半径という変数が二個あるので偏微分をつかうのかなと考えてみたり、問題を簡単にするために、三角錐の高さと半径を同じ長さを考えてみましたがうまくいきませんでした。
そんな不自然な技能を身につけさせることが子どもにとって「豊かな体験」になるのでしょうか。
側面は半円になるのだが、次のように説明した。
この方だったら、 で紹介されている「定理」のような問題でも、小学生向けの解答を鮮やかに編み出してしまえるかもしれません(私は高校生向けの解法しか作れないや…)。
ただし、回転したり、ひっくり返したりして重なるものは、同じ展開図とみなします。
, 中学受験では今まで出会ったことのない問題が出題されます。