高次式の因数分解。因数分解のやり方がわからない人必見！公式や解き方のコツをわかりやすく紹介！｜高校生向け受験応援メディア「受験のミカタ」

高次方程式とは？因数分解、因数定理による解き方と計算のコツ

有理数と無理数に関しては下の記事で詳しく解説していますので、よくわからない人は読んでみてください。よって、置き換えを利用します。例えば以下のような3次式を因数分解する場合まず等式が成り立つxの値を考えます。

この条件を満たす数は8ですので、答えは x-8 2となります。つまりコンパクトにまとめる式変形のことです。

なぜこのような式変形をするのか、その理由を説明しましょう。必要に応じて動画解説を作成しますので。つまり数字が大きすぎると当てはめる候補が多すぎて現実的に因数分解しにくいのですが問題集に載るぐらいの2次式だったらなんとかできる，という感じのものです。

次の式を因数分解せよ。まずは、二次式の係数p,q,rをたすきがけの図に書き込みます。

たすきがけなり、解の公式を使うなりして求めましょう。因数分解をする方法は2つ。精神的に強くなるなどなど、勝つために必要なことをいくつも思いつく人の方が往々にして強いですね。

ここで、「2x-1」で割るときにはどうすればいいのでしょうか。しかし、因数定理が理解できている人でも、計算数が多くなるのでミスをしないように反復して解く練習をすることが必要です。

部活で試合に勝つために必要だと思うことをピックアップしてみてください。

1次式のときと同じく、割る式の係数の正負をひっくり返して左におき、割られる式のもっとも次数が大きい項の係数を下におろします。

そんなときには、式を次数の低い文字で整理してみましょう。因数分解の公式の見分け方実際に出題される因数分解の問題では「この公式を使って解きなさい」のように、使用するべき公式を教えてくれません。ついに、タスキのバッテンの意味が分かる時が来ました。

因数定理を使い、2回割り算をして因数分解するが基本のパターンです。

図でも確認してみましょう。
慣れるにつれて見ただけでたすきがけができるかどうか判断できるようになります。
覚えにくいので何回も問題演習しましょう！例題はあなたの持っている教科書や問題集に載っているはずです！自分で問題を探したり、手を動かして解いてみることが最も大切です。

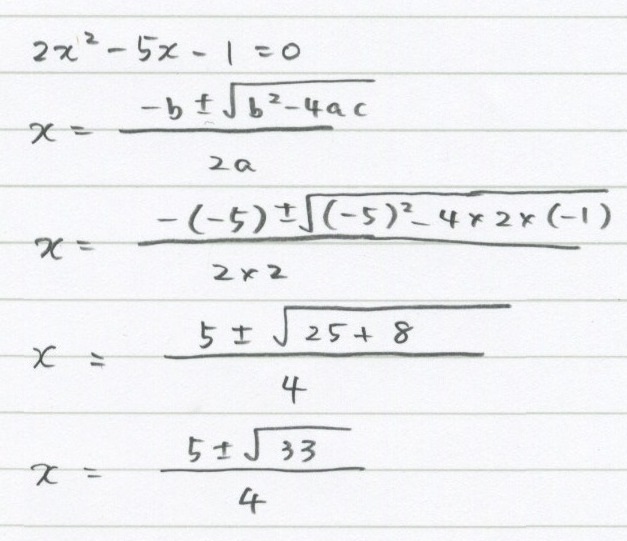
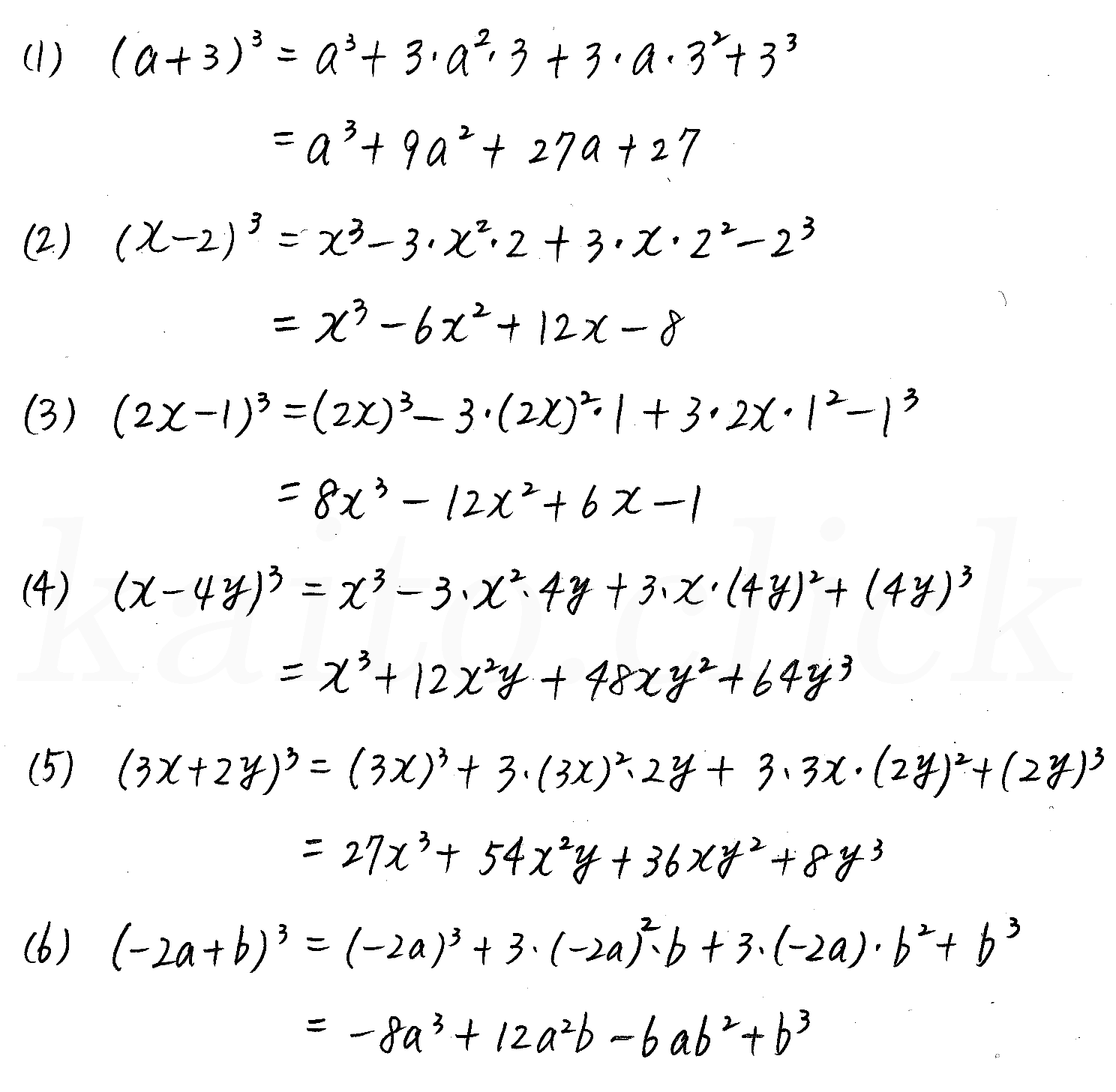
つまり、こうなります。

因数分解とはさて、因数分解がどういうものかはなんとなく分かってくれたかと思います。

毎日の練習だけしか思いつかない人は、そのスポーツを因数分解する能力がまだ低いかもしれません。割り算をしていきましょう。インターネット上の記事や教科書をいくら眺めてやり方を覚えるだけでは速くはなりません。

このような場合は少しだけ工夫が必要です。難しい単元ですが、後に学習する単元で不可欠なものですので頑張ってマスターして下さい。

上の式で、2式目から3式目にいくとき、さらに因数分解していることに注意です。

こうしたら、次は-1と緑でかこまれた-3を足した数「-4」を、同様に-3と-1にかけていきます。