フィボナッチ 数列 一般 項。 【数学】フィボナッチ数列と一般項の求め方｜ペンちゃんとお勉強

フィボナッチ数

詳しいことは追って説明しますが、三項間漸化式の一般項を求める手順は次の通りです。 黄金比とは何か、探っていきましょう。

8

よって矛盾が生じ、仮定が正しくないことがわかりました。 89枚：ミケルマス・デイジー• ） というわけで、HaskellのSemigroupクラスに自乗に特化したメソッドがあるといいなあ〜〜、という話でした。

• 美しいと思う長方形を突き詰めたらこの性質がわかったのか、それともこの性質故に美しいと思うのかはわかりませんが、この黄金比は古代ギリシアやエジプトの建築などで用いられてきました。

• 人の美的感覚（建造物・美術） 古くから黄金比は人間がもっとも美しいと感じる比率と捉えられ、多くの建造物や美術作品に登場しています。

• Koshy, Thomas 2019-01-07 , Fibonacci and Lucas Numbers with Applications, Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts, Volume 2 2nd ed. 100 番目の本当のフィボナッチ数は 354224848179261915075 なのだ。

どこよりもよくわかるフィボナッチ数列の一般項の解法について

この条件の下で、産まれたばかりの1つがいの兎は1年の間に何つがいの兎になるか？ つがいの数は次の表のようになる。

3

このうずまき、なんとなく見たことはありませんか？ アンモナイトやオウムガイのうずまきは、このような形を描いています。

• これがフィボナッチ数列の一般項です！. （植物の葉の付き方）はフィボナッチ数と関連している。

• すると，それぞれの初期値に対する周期が下に出力されます。

• さらに、 n が大きい場合には一般項の公式（上記例3）や行列表現 を利用して （）での計算を行う。

フィボナッチ数列の一般項について

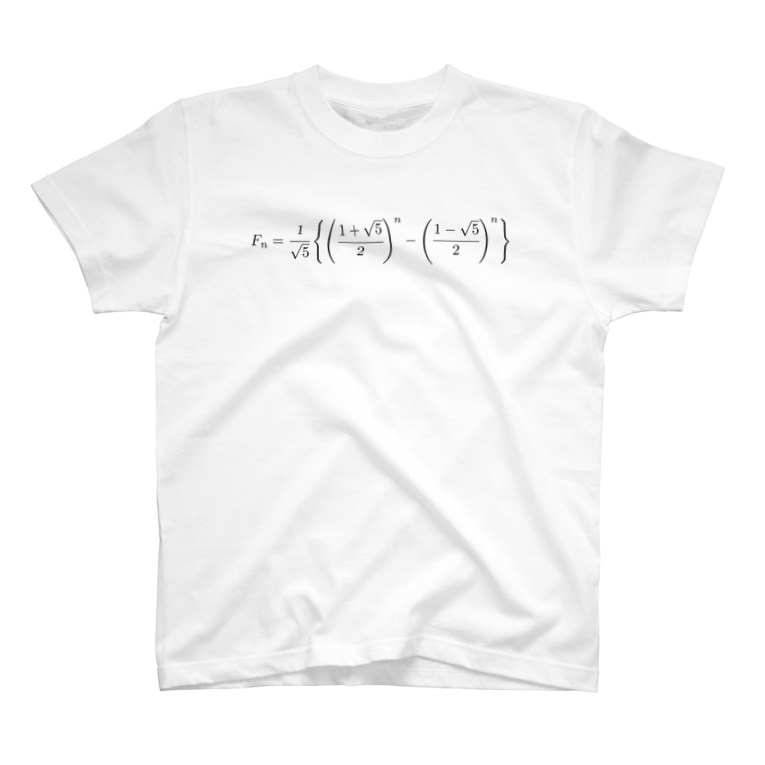
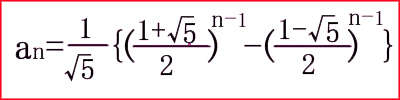
Annales Mathematicae at Informaticae 37: 107-124. より一般に、フィボナッチ数はにもならず 、2つのフィボナッチ数の商も完全数にはならない。 21枚：、• の螺旋の数は時計回りは13、反時計回りは8になっている。

13

次のように表現したはずだ。 黄金分割を説明しました図は，縦横の比を黄金比としました。

• この式より、負の番号の項は次のようになる。

• 以上で解説は終わりです。

• ウサギは満２ヶ月目に子を産みそれから，毎月雌雄１対を産みとき，最初の１対は１年の終わりには何ほどになるか。

フィボナッチ数列の一般項

確かに、いずれの作品も美しいですよね。

4

このようにして、三項間漸化式を解く、すなわち、三項間漸化式で表される数列の一般項を求めることができました。

• これは，a1,a2 の値を，座標平面の格子点ごとに，変化させていき，その点に対する剰余の周期を色分けしたものです。

• フィボナッチ数列を用いた問題 フィボナッチ数列は大学受験で出題されることも多々あります。

• すると、Aの方は• こちらは有理数計算を伴うため、整数演算のみのFastDoublingには勝てないのだろう（推測）。

【数学】フィボナッチ数列と一般項の求め方｜ペンちゃんとお勉強

これがフィボナッチ数列です。 実験用のソースコードは に置いてある。 a だった。

5

全く無秩序に見える自然界も，厳然たる数学的法則に支配されていることが分かります。 Ming, Luo 1989 , , Fibonacci Quart. 27 2 : 98-108 ,• そのウサギは，最初の満2ヶ月は子を産むことができないのですが，3ヶ月後から次々と子を産んでいき，その子も満2ヶ月後から子を産んでいく場合，一体12ヶ月後には何匹のウサギがいることになるでしょうか a 13 を求めよ ？ という意味です。

• 数列は「1,1」から始まり、 1, 1, 2, 3, 5, 8, 13, 21… と続いていきます。

• いかがでしょうか？ このように，黄金比は美しい比率であるとされ，名詞の縦横，ギリシャのパルテノン神殿の縦横，ミロのビィーナスのおへそから上と下の比率に見られます。

• 354224848179261915075 別に 10,000 番目だっていける。

最速のフィボナッチ数計算を考える

初項は3、公比は2です。 演算子を実装する : 累乗 まずやらなきゃならないのは累乗だが、これは乗算の繰り返しの形で表現できる。

1

つまり、黄金比を持つ長方形から正方形を抜くと、また黄金比を持つ長方形が現れるのです。 発想を逆転させて、「一歩前にどこにいるか」を考えるべきなのです。

• 漸化式 漸化式 ぜんかしき とは再帰関係式である。

• 一般項（ビネの公式）による計算法を高速化する フィボナッチ数列の一般項（ビネの公式）を再掲しておく。

• 上の例は，音楽の世界の例ですが，自然界には，多くのフィボナッチの数列が潜んでいます。

フィボナッチ数列の一般項を計算する(※ただし有理数に限る)

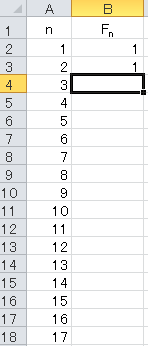
ここで三項間漸化式の解き方を復習しましょう。 フィボナッチ数列の特徴 では、フィボナッチ数列の特徴を説明していきます。 Fibonacci and Lucas perfect powers. 出典 [ ] "Acharya Hemachandra and the so called Fibonacci Numbers". フィボナッチ数列の一般項を求める場合、先ほどの漸化式を解くのと手順は全く変わりません。

15

表記がちょっと見づらい。 はじめに これはの22日目の記事となります。

• と続くアレだ。

• のやに現れるの数もフィボナッチ数であることが多い。

• この渦巻きは，カタツムリの殻や，オウムガイに見ることができます。