三角比の相互関係。三角比を用いた計算問題をマスターしよう！｜スタディクラブ情報局

【数学Ⅰ三角比】sin cos tanの相互関係と覚え方

しかし，２乗を計算するのは簡単です。相互関係の3つ目の式を使うと、次のように計算できます。上の相互関係を順に確認していきます。

式の値を計算するものについてまとめました。

様々な三角比の四則演算例題の値を求めよ。
複雑な方からスタートして式変形をし、簡単な方に変形してクリア、というのがよくある流れです。
三角比だけからなる関係式です。

高校数学Ⅰ 三角比の相互関係まとめと問題

2 の三乗＋三乗は、因数分解の公式を活用します。三角比の相互関係のまとめさいごに、三角比の相互関係のまとめをします。

様々な三角比の四則演算• 等式を証明するもの• 解答であるからより示された。

そうすれば、ど忘れなどは一切無くなります！ 3. 三角比の定義の覚え方三角比の値を覚える方法として、筆記体を利用した覚え方があります。
上の問題では右辺を左辺に変形していきましたが、どちらが平易かは問題次第。
三角比に慣れるまでは、このような方法も知っておくと便利ですね！三角比の拡張さらに、もう少し三角比の考え方を拡張してみます。

【数学Ⅰ三角比】sin cos tanの公式まとめ（表・変換・相互関係・面積・正弦定理・余弦定理）

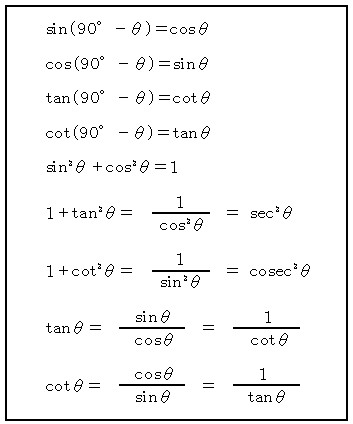
（参考：）• 一つ目の式は正接（ tan ）の定義から直ちにしたがうものです。

。

赤線を斜辺とする直角三角形で三平方の定理を使います。
角度の範囲に注意して、適切な符号を選択しましょう。
それを考えるために使えるのが 2 でつくった方程式です。

三角比の相互関係

本記事で取り上げた問題はどれも定期試験頻出。単位円を描いて、上の公式を確かめてみましょう。

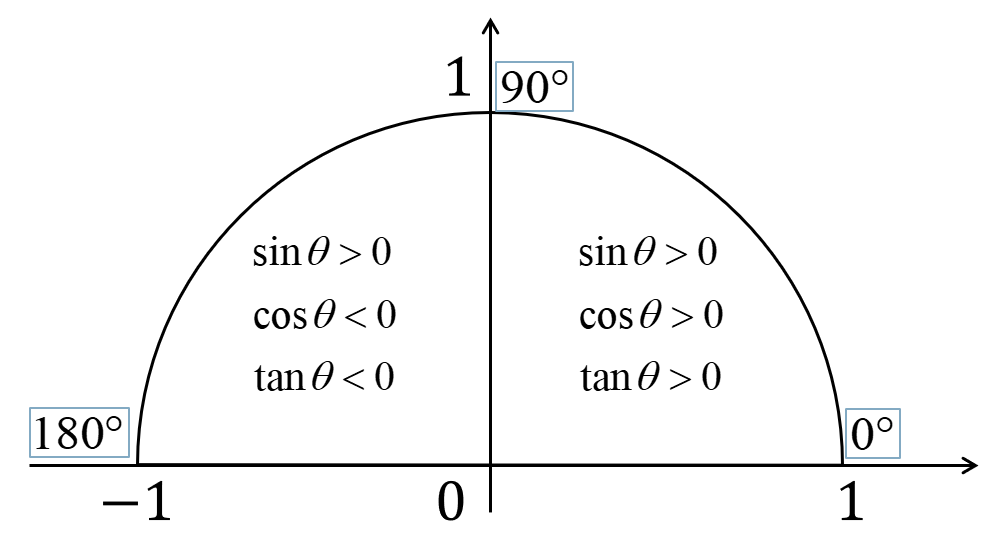
まとめ三角比を用いた代表的な計算問題• 基本公式のおさらい次に、三角比の基本公式を復習します。この考え方は後で紹介する三角比の相互関係を求めるときにも利用するので、単位円の書き方とともに理解しておいてください。

三つ目の式は、二つ目の式をで割り算したものです。
相互関係異なる三角比の間には、次のような関係が成り立ちます。
逆に、複雑な結果になってしまったら「どこかで計算ミスをしていないかな？」と自分でチェックするようにしましょう。

【数学Ⅰ三角比】sin cos tanの公式まとめ（表・変換・相互関係・面積・正弦定理・余弦定理）

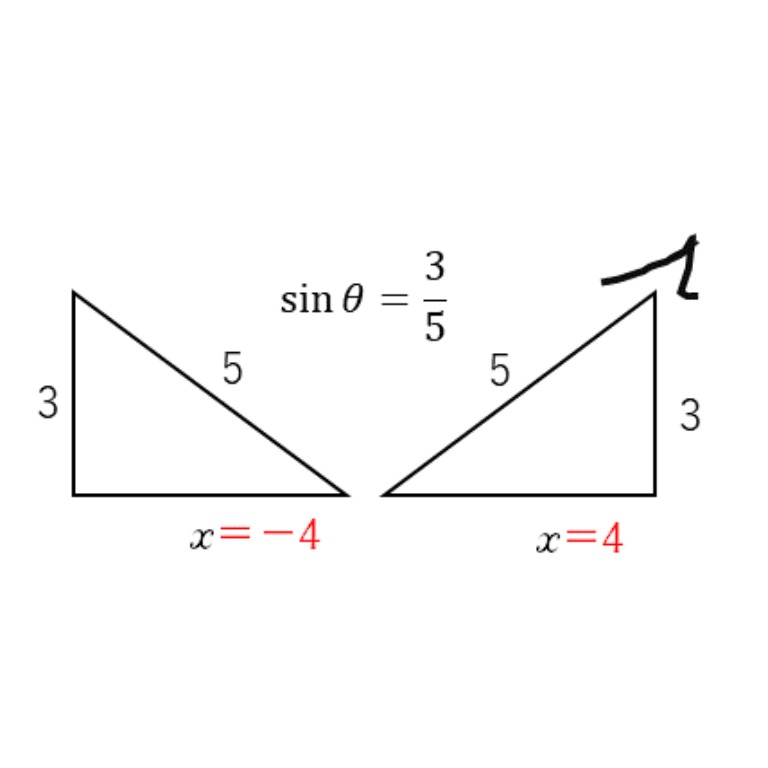
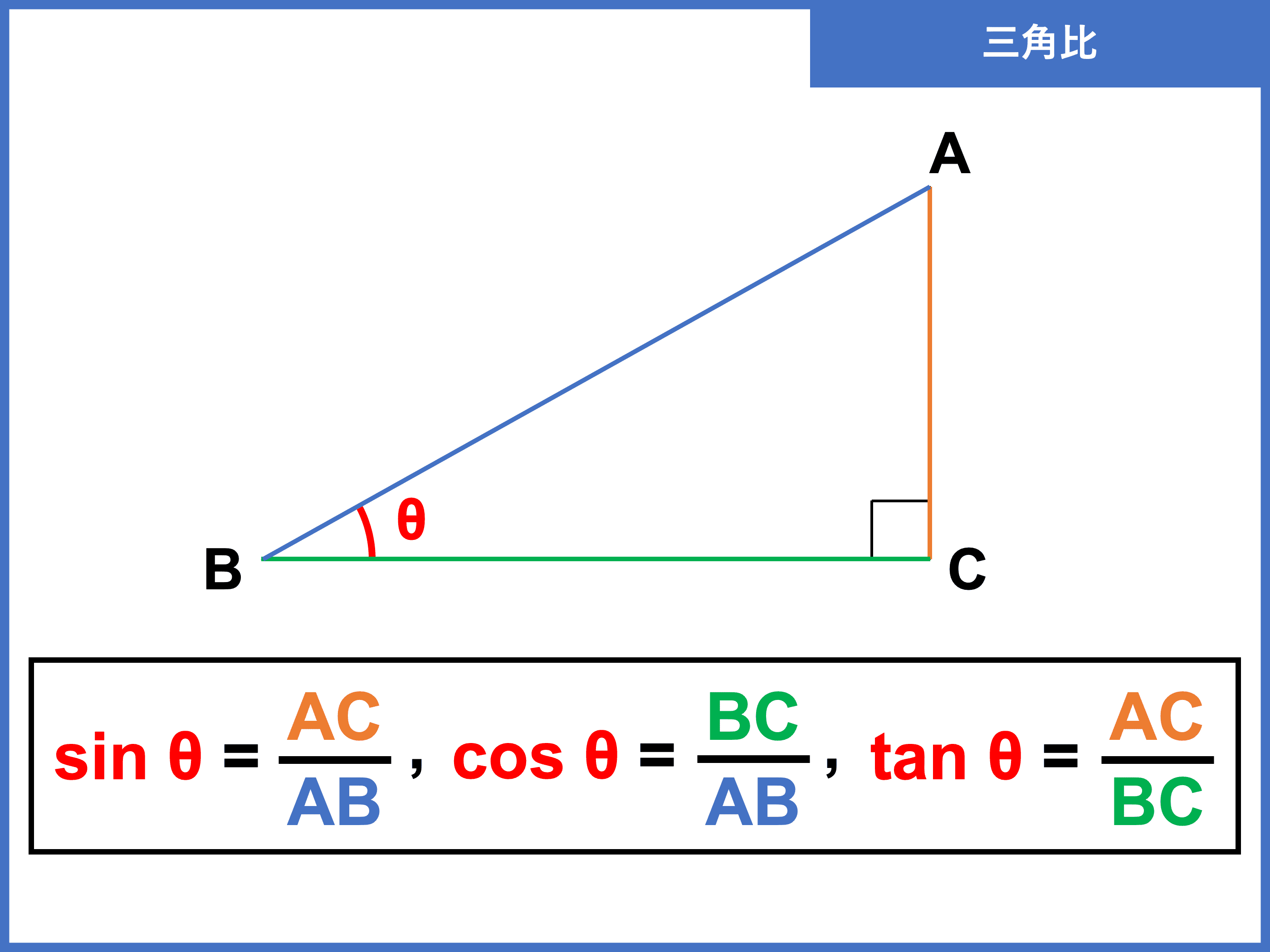
途中で符号や sin, cos のミスがあると途端に複雑になってしまいます。解答であるため、したがってであるからまたであるからポイント三角比の相互関係を用いて他の三角比を求める場合、符号の選択をする必要があります。題意の２次方程式はいくつもありますが，最も簡単なものを考えます。

1 2 3 解答 1 の両辺を二乗するとも合わせると 2 1 の結果を用いると、 3 のときであるから、よりゆえに 1 よりよって、ポイント 1 での両辺を二乗するのが山場。三角比の相互関係の覚え方初めはなかなか覚えづらい三角比の相互関係ですが、式の導出方法を知ると意外とすんなり覚えられます！三角比の相互関係は、単位円における三角比の定義式から簡単に導けます。