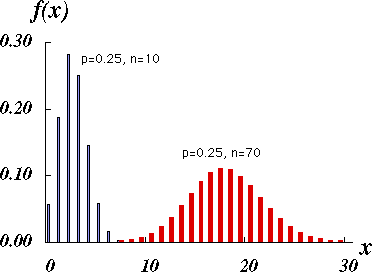
負の二項分布(グラフ)

さらに言えば、平均と分散を計算しただけなら別に母関数を使わなくてもできる。 が二値に名義関数のデータで想定されることが多いのに対して負のやボアソン分布は個数や回数のデータで想定されることが多いです。
12

さらに言えば、平均と分散を計算しただけなら別に母関数を使わなくてもできる。 が二値に名義関数のデータで想定されることが多いのに対して負のやボアソン分布は個数や回数のデータで想定されることが多いです。
12式書くのめんどくさいので以下スクショ。
あれ、kには期待値記号が付くのにrに付かないのはなぜ?と思う人もいるかもしれないが、現在の定義だとkについての関数になっていてrは固定値なので期待値記号は付かない。
これら5つの式は割と簡単に導くことができる。
理論的確率分布は、統計的実験の各可能な結果に確率を割り当てる関数として定義されます。

ポアソン分布の定義 1830年代後半、有名なフランスの数学者Simon Denis Poissonがこの分布を紹介しました。 まずは階乗の部分をガンマ関数に ガンマ関数についてはぐぐればいくらでも出てくるので詳しくは書かないけど、これを使えば階乗の概念を連続的な量に拡張できる。 この変形によってどれだけすっきりしたかイメージできるだろうか。
9これは cX についての 負の二項分布です。 各分布の詳しい情報は表の中のリンクからお願いします。
そうすれば連続的な関数として取り扱うことができるようになるはずだ。
試行は独立した固定の正の整数です。
ただし住民は500人よりずっと多いとする。
確率 p で成功する独立なが繰り返された時の成功回数の分布を表すという意味でによく似ているが、負の二項分布では試行回数があらかじめ決められておらず、 r 回の失敗が起こるまで試行が続けられる。 一方、 ポアソン分布では、考えられる結果に制限はありません。
同意する人数の割合は、もちろんサンプルに依存する。
ここで、nは繰り返し試行、pは成功確率です。
一方、ポアソン分布には無制限の試行があります。


ちなみに、モーメント母関数から計算しても、別の定義の負の二項分布から計算しても同様の結果を導くことはできる。 確かにグラフで見たのと同じように、期待値は 35 になります。
そのため、 stan 関数を実行すると失敗する可能性がある。 05 の二項分布に近似的に従う。
ここで、発生は成功と呼ばれ、発生しないことは失敗と呼ばれる。
。
全部の定義でやるのはかったるいので、1番目の定義に絞ることとする。

しかし、運が悪ければ、とても少ない確率で、選んだ500人の中にたまたま一人たりとも患者が含まれないような、真の分布とかけ離れた分布が得られる場合もある。 これをn回微分すればn次のモーメントが求まる。
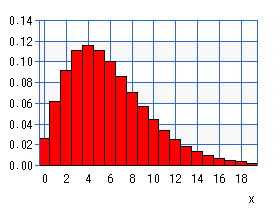
1例えば、メスの産卵数のデータは50個のメスのデータで計算したら、50こあることになります。 5で1回成功するまでに失敗した回数としてその回数が0回である確率、1回である確率、20回である確率までを計算して、それらをまとまてyに代入します。
そのため、カウントデータをモデル化するときは、単回帰のように分散が常に一定の確率分布ではなく、平均が大きくなると分散も大きくなるような確率分布でモデル化する必要がある。
試しに1つ目の定義について考えてみる。
この試行をAと呼ぶことにします。


下記は、0~2回の累積確率を計算するRスクリプトです。 さらに、パラメータの値に基づいて、両方とも単峰性または二峰性であり得る。 二項分布については使われる機会も多く、少し調べてみると充実した解説が山ほど出てくるが、負の二項分布についてはあまり充実した情報はないようだ。
11せっかくなのでもう少し踏み込んでみよう。 例えば、多数の住民の中から n 人を無作為に抽出し、ある質問について同意するかどうかを尋ねる場合を考える。
この試行をBと呼ぶことにします。
ただ、俺はキュムラント母関数が便利で応用がきくので好きだ。
r は正の整数で、 p は 0 から 1 までの実数である。