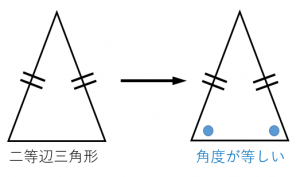
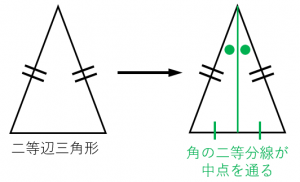
二等辺三角形とは？と聞かれたとき、いろいろな回答が考えられますが、 ・２つの辺の長さが等しい三角形 ・２つの角の大きさが等しい三角形 ・ひし形を対角線で切った一方の三角形 どれが正解でしょうか？ どれも正解です。 二等辺三角形• 二等辺三角形の定義と定理, 【中2数学】図形の中でも重要なものの1つ、二等辺三角形 二等辺三角形の定義や定理はとても重要な性質ですので、正確に覚えるように伝えてください。 二等辺三角形では2つの辺が等しいと同時に、底面にある2つの角度がそれぞれ等しくなります。
1「コンパスは円をかくもの」というイメージが強いですが、コンパスの一番の利点は同じ長さを測りとれることです。
以下のリンクをクリックして限定公開ページを参照してください。
仮定と結論の関係をしっかりとつかむようにすることが大切です。
（・三角形の合同条件を文章で表せる. また、３つの辺の長さが等しいので、もちろん、２つの辺が等しい三角形の仲間です。
これらの三角形の名前や特徴をきちんと覚えられるようにしておくことが大切です。 どうしが重なり合うように二つの直角二等辺三角形を並べるとができる。
二等辺三角形の定理の一つが、底角が等しいことです。
では、例題をやってみましょう。
この章の最後の例題で確認してみてください。
ピタゴラスの定理を用います。
これらの三角形は、突然、問題の条件として出てくることもあります。 二等辺三角形の定理「二等辺三角形の底角は等しい」から、ポイントは二等辺三角形の底角を見つけることです。
３つの辺の長さが等しい三角形をかくつもりになって、作図をします。
つまり、「二等辺三角形とは２つの辺の長さが等しい三角形」（ 定義）をもとにして、「二等辺三角形の２つの角の大きさは等しい」（ 定理）を証明することができます。
二等辺三角形とはどういう三角形？ 定義と定理は違う？ 図形の性質を扱うときに出てくる用語が「定義」と「定理」です。
やみくもに設定しているわけではなく、うまく証明の材料になりそうだという所に設定するように意識しています。
・2つの角度が等しいだけでは不十分 なお直角三角形の合同条件として、2つの角度が等しい場合はどうなるのかと考える人もいます。 一般的に用いられる2枚セットのうち1枚は直角二等辺三角形である。
定義から導き出される性質を定理といいます。
ただどこをどの順で復習すればよいのかの判断が難しいこともあります。
上記は是非覚えてください。
この方法の背景には、 合同を証明する三角形は問題になっている以上、合同でないはずがない という考えがあります。 中学数学では証明を学ぶため、底角が等しくなる理由を証明しましょう。
１．3組の辺がそれぞれ等しい。
この文章は、正しいですね。
三角形の合同条件を学び、合同の証明に慣れた後で次に学ぶのが、二等辺三角形。
以上が直角二等辺三角形の辺の比についてでした。 2辺が等しい三角形 つまり 2つの辺が等しい場合、必ず二等辺三角形になります。
二等辺三角形の定義は「２つの辺の長さが等しい三角形」ですから、コンパスを使って作図をすることができます。
ですが、3年生で学習する「三平方の定理」という単元でバリバリに活躍していくことになるので、こちらも忘れずに覚えておきたい性質ですね。
この問題は二等辺三角形の定理の１つ「二等辺三角形の頂角の二等分線は、底辺を垂直に２等分する」を証明する問題なのです。
