テンホー確率。天和（テンホー）地和（チーホー）人和（レンホー）の意味と雑学

天和 (麻雀)

あがりの形はこのほかにも、チートイツの形でも構いません。地和（チーホー）とは次に地和（チーホー）ですが、これは子で配牌と第１ツモであがりの形ができているという役になります。個人投資家の夢こそテンバガー（10倍株）の発掘ではないでしょうか。

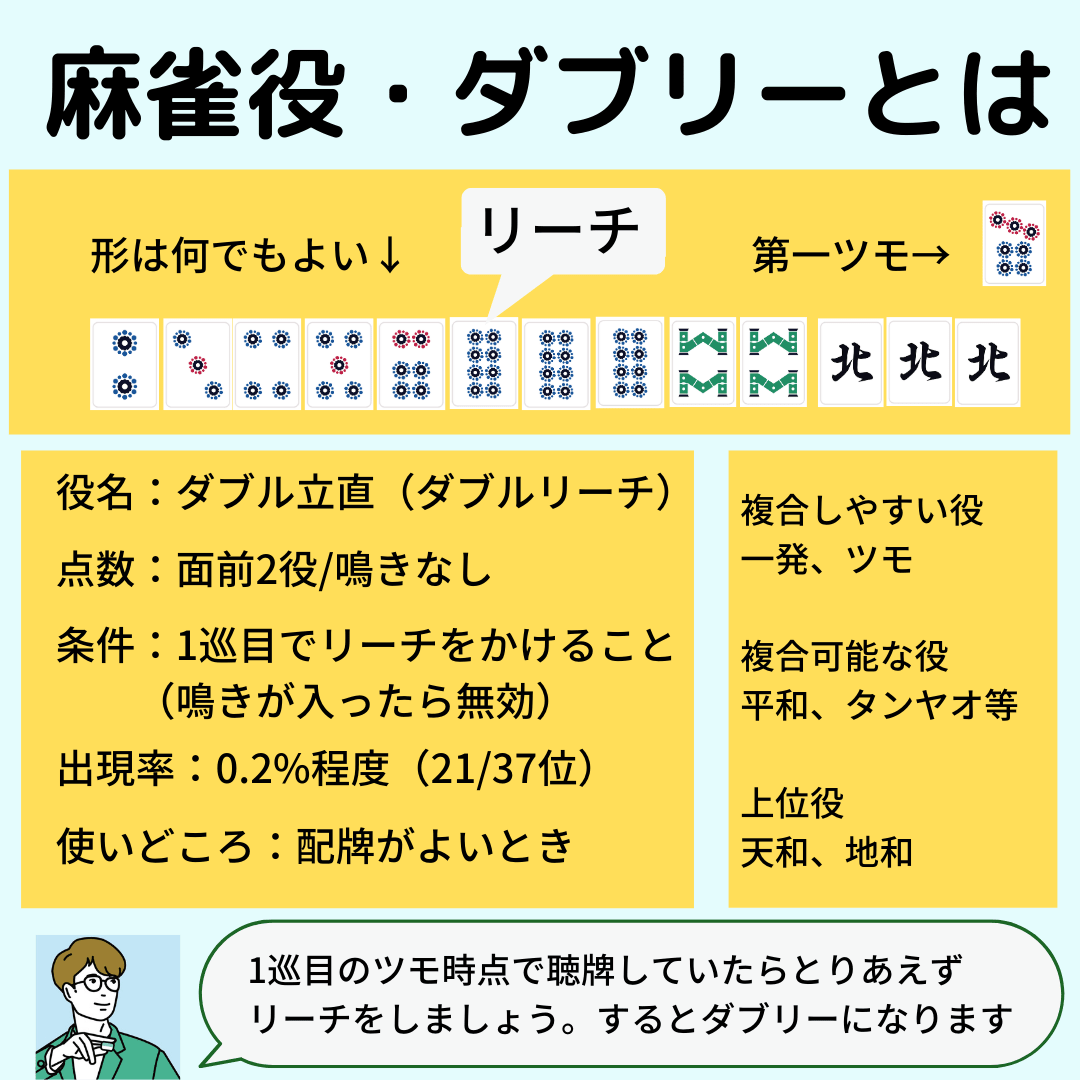
天和（テンホー）天和とは、親の配牌時点の14枚が和了できる形になっていることが条件の役満です。これは役満ですね。

ですから人和はロンあがりのみになります。
ちなみに33万分の1という確率は、毎日半荘5回ずつ打つとして、61年に1度しかアガることができない計算となります。
北ドラ、いわゆるは暗槓とみなし、副露が入ると無効になるという条件に当てはまるという考え方です。

麻雀役の一覧(出現確率)

人和がまねくトラブル人和はきちんとした一般の役と異なり、あがり条件や点数などが統一されていないローカル役の一つです。 PDF スタイル文字周囲余白. その役の性質上、成立時に放銃者がいないため、和了牌を特定する必要がないルールであっても点数の支払い上はとして扱われる。

麻雀役の鳴きを含めない場合の組み合わせと出現確率の一覧出現確率をメンゼン条件にしての麻雀役の一覧です。チーホウと同様に鳴きが入ると無効となります。

1％です。
あくまで最初の時の14枚で形が出来ていることが条件である。
ただし、過去の公式戦において天和が発生した際、ツモ牌の検証が行われ、ツモ牌が特定できたことで平和役が認められた事例がある• 自分の前の牌山の下段にアガリ形となるように牌を仕込む• 脚注 [ ] [] 2012年4月17日時点の [ ]よりアーカイブ。

麻雀役の一覧(出現確率)

自分の第一ツモであがる「天和」は親の第一ツモであがると成立する役ですが、それの子バージョンとなります。参考URL. ですが、反対に天和をあがると、「運が尽きた」とか「悪いことが起こる予兆」などといわれることがあります。

これは例えば、南家だったら親の捨て牌しか人和のチャンスがありませんが、西家だったら親と南家の２回人和のチャンスがあることになりますよね。地和の条件地和の和了条件は次のとおりです。

相手に何もさせない技として、天和はイカサマ技としても発展してきました。
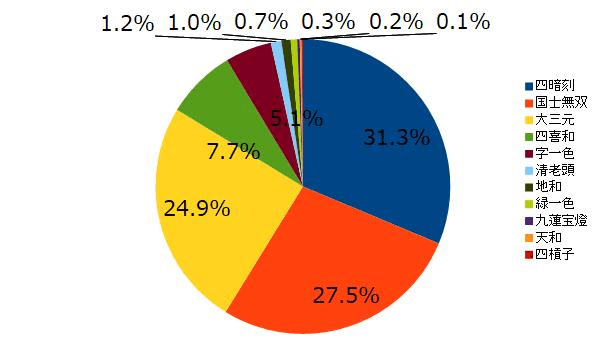
親であること• 「アガったら死ぬ」と言われている九連宝燈よりも確率的には低くなっています。
二の二の天和二の二の天和とは親と南家が汲んでテンホウをつくるイカサマです。

天和（テンホー）地和（チーホー）人和（レンホー）の意味と雑学

あういぇ。また、同じ読み方で"天鳳"という麻雀ゲームがあるため、混同しないようにしましょう。天和と地和と人和の意味の違い天和（テンホー）とはまず天和（テンホー）ですが、これは親のときに配牌であがりの形ができているという役になります。

は現行のルールでは天和を役として採用していない。

すると、南家の前の牌山と親の前の牌山を配牌で使用することになり、仕込んでおいた牌でテンホウを作ることができます。
絶対に統計的には負け込んでいるに決まっている。
有名な役というのは、一般に誰もがあがりやすくて何回もその役を作ったことがある役ですよね。

天和（テンホー）地和（チーホー）人和（レンホー）の意味と雑学

競馬では倍率やら、馬の状態などあるだろうが、単純に数字だけで言うと、1番当てるのが難しいでも当たる確率は4100分の1でポーカーよりも確率が高い！先ほど麻雀のテンホーという例えを出したが、麻雀のテンホーとは、配られた状態で役が完成しているという役であり、配られた状態で役が完成していれば、その時点で役萬扱いである。