不偏標準偏差とは?:統計検定を理解せずに使っている人のために


ところが,実際には,不偏分散の平方根を不偏標準偏差と呼ぶ人が結構いる。
18平均だけではデータを活かせない 前述したとおり、5日間の平均売上は7,200円。
分散は求める過程で、二乗が行われているので、本来の単位とは単位が異なり、そういう意味では少々分かりにくい指標となっています。
以下では、「なぜ n ではなく n-1 で割るのか」ということに焦点を当てて解説します。
僕は面倒なのでやりません、あ。
すると、なぜ「データ数-1」なのかという疑問が生まれますが、「やってみたらそうなった」ということですね。 具体的には、 標本分散は母分散よりも小さくなる という性質に由来します。
実際に計算してみると、10で正しいことがわかりますね。
「精度よく推定」とあいまいな表現を使っていますが、推定について数学的に考察すると非常に難解になってしまうので、とりあえず「不偏分散で真の分散を推定できる」ということを知っていれば差し支えありません。
上式の についての平均をとれば となり、また、繰り返し測定変動誤差の偏差平方和 は となります。

+×+×+×+×+×+×+×+×+×+×+×.jpg)
そこで、 「本当に真の分散は 0. 「ばらつきが小さい」ということは、分布を描いたときに、「正規分布に比べ山の頂点が高い曲線を描く」ということです。 偏差値とは、その数値がデータの中でどの位置にいるかを示したもの。
23 1項目については、 4 また第2項目はより、 5 これらより、標本分散の期待値は以下のようになる。 同じく、Excelのダウンロード数から、どれだけの母集団が存在するかを、VAR. しかし、この説明では、たまたま、この一つの具体的な現象において、N-1で割るほうがよりよいと言っているだけであって、他の場合すべてにおいてもより良いことの証明になっていないと思いました。
分散の推定 7 母分散の推定 n-1で割る理由 母集団の情報を得るために,母集団から無作為標本をとるしか手が出せません。
それでは、平均値からどれだけ離れているかを表す指標として適切ではありません。
標本から母集団の分散を推定した分散を不偏分散という 不偏分散の名前の由来:分散の不偏推定量だから 不偏分散という名前は、不偏分散分散の不偏推定量であることに由来します。

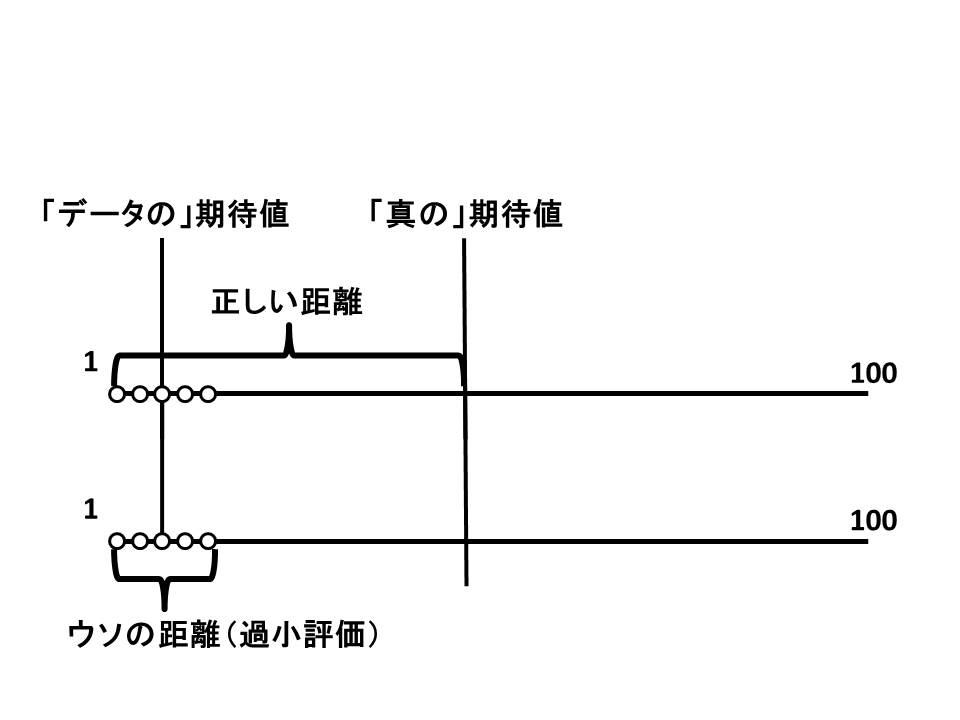
標本の分散を標本分散という• 不偏分散・・・標本から予測した母集団の分散 という返答になるのですが、「標本分散と不偏分散の違いってなに?」と聞かれても答えるのが難しいのです。 データから母集団の性質を推定したいとき:不偏標準偏差 or 不偏分散平方根 標準偏差と分散の関係については、こちらの記事をご覧ください! >> 不偏分散に関してエクセルでの関数は? 最後に、エクセルで分散または、不偏分散または不偏標準偏差を用いる時に使う関数について紹介します。 平均値が3. さて、不偏分散を計算する理由を、下図を使いながら見ていきましょう。
12なんとなく分かりやすいです。
プログラム 1. 画像はエクセル 2016のものです。
まず、下の画像のように、個々のデータを2乗した値を書きます。
com• どれくらいの人がダウンロードしたのか? 2020年10月24日時点で、私のYouTubeのチャネル登録数は。


分散の意味と求め方、分散公式の使い方 sci-pursuit. しかし、真の値(中央値からの平均距離の二乗)は1のはずだから、分母のNを小さくせねばならない。 分散の公式 分散の計算は公式の通りにやれば何も難しいことはありません。
7このように、 データを代表する値のことを 代表値といいます。
有料の統計解析ソフトさえあれば、統計解析はできるようになる これらは、私が医療従事者を中心に統計を教えてきた中で、統計解析に対する間違ったイメージの典型例です。
この c 4 の逆数が,大村(2014)が言う 水増し係数に相当する。
この c 4 は, 管理図(Control chart)係数として使われるものである。
得られたデータから不偏分散を計算する• 1以降と何かで読んだ覚えがあるので、 それが原因だと思います。 電卓を使う場合、不偏分散を下記のように変形した式を用いると、早く計算することができます。
平均を求めるプログラム例は、以下のようになる。
したがって, は不偏推定量とは言えません。
不偏分散の求め方と利用場面 初めに不偏分散の求め方を確認します。

こうすることによって、平均値から離れた値をとるデータが多ければ多いほど、分散が大きくなります。 2段目は6個のデータそれぞれを 2乗した結果とその合計 和)です。 SELECTしたデータの不偏分散を出したいのですが。
1075 続いて 2.変数sとtについて次の観測値があるとする s -5,1,3、-1、-7 t -1,2,5、-7,11 1 sの標本分散を求めよ 2 tの不偏分散を求めよ 3 sとtの不偏共分散を求めよ 4 sとtの相関係数を求めよ これも自分で算出しました 1 16 2 45 3 ???? 4 ここで質問です。 標本から母集団の性質を推定するために、 不偏推定量というものが用いられます。
平方和の計算では、「庭にひくサンプル分のワニ」を利用してみてください。
つまり、「母集団の分布図」と「標本の分布図」は「違う分布」になるということです。
それに関しては,私の別ページの解説を参照して欲しい。
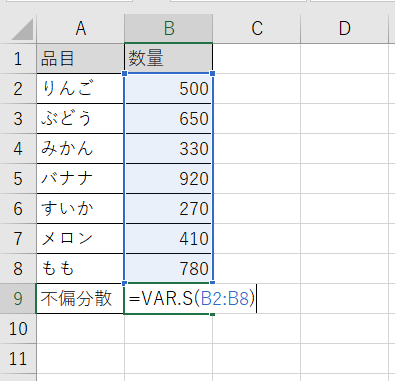
828427 sqrt で平方根を計算することができます。 このことから、母分散に対する不偏分散 は次式で表される。 平均点というのは、合計を個数で割り、ひとつあたりの数を計算したものです。
5になる。 数学の試験で、平均点から、どれくらいの散らばるのか? 統計学的に言うと、母集団が、データ全体そのものであるときに使います。
語呂だけ覚えても意味ないですよね、おぼえる数式は下の式になります。
ただし、主効果 の母平均は でその母分散は 、また偶然誤差 の母平均は でその母分散は とします。
そして、t分布のところで話しましたが、母集団の分布というのは、自然界一般の法則に従い「正規分布」を前提としていましたね。