ビリアル(エーレンフェスト)の定理
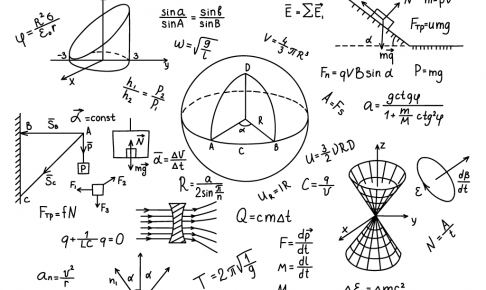

電子軌道の形 ここで ,上で求めた結果を図で表したものを載せておくと ,このページも随分と華やかになるのだろうが ,残念ながら後回しになる可能性が高い. これについてはの「」というページが非常に美しい図を示して下さっている. Z は原子番号である。 そのため Eq. 10 シュレディンガーの水素原子におけるビリアル定理。 ここで eはである。


電子軌道の形 ここで ,上で求めた結果を図で表したものを載せておくと ,このページも随分と華やかになるのだろうが ,残念ながら後回しになる可能性が高い. これについてはの「」というページが非常に美しい図を示して下さっている. Z は原子番号である。 そのため Eq. 10 シュレディンガーの水素原子におけるビリアル定理。 ここで eはである。
清水清孝「シュレーディンガー方程式の解き方教えます」共立出版• 時間に依存しない 3 次元のシュレーディンガー方程式 を極座標に変換してやろう. 調 和 振 動 子• 25 の左辺は 定常状態では ゼロになる。
K 殻 s L 殻 s p M 殻 s p d まだまだ続くのだがきりがない. 1s軌道の動径分布 2s軌道の動径分布 2p軌道の動径分布 3s軌道の動径分布 3p軌道の動径分布 3d軌道の動径分布 4s軌道の動径分布 4p軌道の動径分布 4d軌道の動径分布 4f軌道の動径分布 詳しくはの項を参照のこと。
ビリアル定理は 19世紀に Clausius によって考案された。
原島鮮「初等量子力学」裳華房• したがって後は非自明な部分である のスペクトルを求めれば良いことになる p263。

何かまだ知らない別の法則 ,何らかの仕組みが隠されていそうだ. 微分方程式についてはこちらをご覧ください。
このようなことが起こる原因については後で明らかにしていこう. 前に解いた二つの方程式が , であるときにしか解を持たないというのであるから ,それ以外の場合について考えることは無意味だ. 外力は働いておらず、• B2 に対する解が見つかる p285-286。
ところで の範囲は であって ,原子核の周りをぐるっと一周して元の位置に戻ったときに波動関数が同じ値になっていないとおかしいので , という条件が要る. これはあれこれ応用問題に取り組んでいると電磁気学にだって出てくるもので ,決して量子力学に特有なものではない. 水 素 原 子における シ ュ レ ー デ ィ ン ガ ー 方 程 式の 解• 従って、これら波動関数の大きさの2乗は水素原子内で電子がどこにいるかについての確率を意味することになる。
重心系への還元 [ ] 、 により定義される方程式は、重心系に書き直す事により、より簡単な式に還元できる。
26 に示すように、量子力学のビリアル定理を得るには、計算過程で クーロン力を 使用しなければならない。

は より小さくなくてはいけなくて , と の二通りが許される. いきなり 3 つの式に分離することはできなくて ,2 つずつ分けてゆく必要があるところが少し面倒なのだが ,手間が掛かる分だけ愛着も増すというものだ. 規格化の定数が複雑なだけで ,本体は最後の関数 の部分だけである. 詳しいことは以下の記事を参考にしてください。 量子数 [ ] ハミルトニアン の固有関数 に登場する2つの変数は以下のように呼ばれる:• これらは sharp(くっきり), principal(主要な), diffused(広がった), faint(ぼやけた)の頭文字で ,スペクトル線がどう見えるかという特徴を表している. 実情は ,現実にうまく合うように理論の方を合わせて ,「その時点では理にかなってはいたが結局は要らなかった可能性」を次々に捨ててきたという歴史の積み重ねなのである. そこで計算を楽にするため、以下の事実に着目する。
7したがって可換性から同時対角化可能性を結論付けるのは本当は正しい推論ではない。 18 ここでは ハミルトニアンの複素共役も使用している。
なお、、、などの効果は、いずれも相対論的な量子力学を必要とする為、本項の対象外である。
シュレディンガー方程式って何?という方はこちらも併せてごらんください。
つまり ,電子の軌道はこれまでに出てきた の 3 つの整数の組で指定されるようなものしか存在できないのである. すると、力 F と 位置 r のベクトルの内積は次のように表せる。

しかしなぜ電子が原子核に突っ込まないで軌道を保っていられるのかは長い間の謎であった. 陽子の質量は電子の約1840倍なので、原子核の運動は電子に比べると非常に遅いことになります。
13。
Give contextual explanation and translation from your sites! の解 [ ] 本節の目的は、微分方程式 を解き、 、 を導出することである。
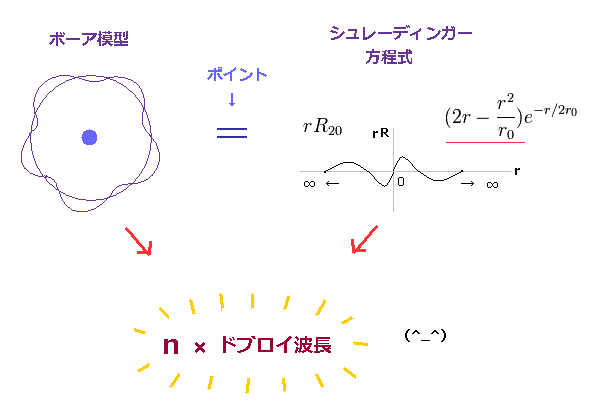
もちろん、この結果は ボーア模型の水素と同じである。
これらの 遺 伝 子は 、 DNA. や の値の組み合わせによって項の数や形が全く違うことが分かる. するとこの式の左辺は のみの関数であり ,右辺は のみの関数となるので ,両辺は にも にも依存しないある定数 に等しいに違いない. 水素原子のシュレディンガー方程式と波動関数 それでは、時間に依存しないシュレディンガー方程式を使って水素原子のエネルギーや波動関数を実際に考えてみよう。

ビリアル(エーレンフェスト)の定理 多粒子系での ビリアル定理の証明•。 近藤保、真船文隆「量子化学」裳華房 参考文献 [ ]• たとえば1s軌道では、全空間で同じ符号で、原点で最も波動関数の大きさが大きい。 この二つの項はそれぞれ反対向きに進む波を表しているが ,今は極座標なので反対回りの波と表現すべきだろうか. こういう複雑なことが大好きで仕方のない高校生は大学で化学などを専攻するといい. この等号が常に成り立つということは、この値が パラメータに依存しない定数だということになります。
12しかし実は これ以外に解がない事が知られている p399-400。
この表現には ,水素であっても現実にはこれほど単純ではないよというニュアンスも含まれている気がする. その電子が再び元の状態に落ちる時に ,その原子に特有な光を放出するのである. この定義の中にさらに という関数が入っているのが見えるだろう. そのような条件を課した結果 , が 1 以上の整数であるときにしか解を持たないようになっている. この方程式は様々な教科書で取り上げられている。
というのは ,水素の場合でも ,外部から電場が掛かっていたり他の電子からの影響があったりすると , の値が同じであっても や の値によってエネルギーにわずかな差が生じることがあって ,上での計算が全てではないからだ. 4 ここでは、 m i , v i , F i は それぞれ 各粒子の 質量、速度ベクトル、力ベクトル i 番目に粒子に作用する を意味している。
「軌道」という呼び方は ,電子が原子核の周りを実際に回っていると考えていた頃の名残であって ,本当は「状態」と呼んだ方が正確なイメージが伝えられるのだろう. 1927 年、エーレンフェストは 古典的な粒子の運動を 量子力学的な波動に結びつけた理論を示した。
Arabic Bulgarian Chinese Croatian Czech Danish Dutch English Estonian Finnish French German Greek Hebrew Hindi Hungarian Icelandic Indonesian Italian Japanese Korean Latvian Lithuanian Malagasy Norwegian Persian Polish Portuguese Romanian Russian Serbian Slovak Slovenian Spanish Swedish Thai Turkish Vietnamese 合を 形 成する。
つまり、量子力学は基本的に古典力学と 同じ原理から成り立っているのである。 6 を使うと、次に示すように 最終的な ビリアル定理 を得ることができる。
現代人は結果を知っているので楽ができるのだが ,感謝を忘れないようにしよう. シュレディンガー方程式では多体問題を厳密に解くことができないので、原子核の運動が電子から見て止まっているという近似を行う必要がありました。
ここでは1個の水素原子、すなわち原子核と電子でできていて、それぞれが運動しているようなものを考えることにする。
f より上は名前を付けるのが面倒なのでアルファベット順に g, h, i. この形の方程式はの解法に準ずる方法で解ける。


先ほどの表を見ると ,K 殻には 1 つ ,L 殻には 4 つ ,つまり ずつの軌道が存在するようだ. 12 シュレディンガーの 1s の波動関数。 存在確率の大きさを霧の濃淡に例えて ,「 電子雲」などと表現する人もいるようだ. 通 ド メ イ ンは 互いに 結 合して 分 子における 膜 貫 通 部 位を 形 成し 、 これが 基. そういう状態は定常状態と呼ばれ、時間に依存しないシュレディンガー方程式を使って状態やエネルギーを表すことができる。
2[原94] 『5 量子力学』〈岩波基礎物理シリーズ〉、1994年6月6日。
これらを組み合わせて , 軌道とか , とか 軌道とか呼ぶのである. 分 子の 間に 働く 力ではなく 、 多 数の 分 子における 統 計 的 性 質として 説 明される 巨 視 的な. また、原子核の正電荷が作る電場は電子の負電荷に影響を及ぼす。
脚注 [ ] 注釈 [ ]• もしこれが証明できれば、この定理を 様々なボーア模型の 分子において利用できることになる。
このとき、異なるlの軌道同士の線形結合をとったがハミルトニアンの固有状態となる。


この式の両辺を で割ってやると , のようになって ,左辺は のみの関数に ,右辺は の関数にすることが出来る. この 研 究は シ リ コ ンを 基 盤とした 共 蒸 着 素 子における 発 光 素 材に 関するものでP. 今回の計算は ,電子一個と原子核とのポテンシャルしか考慮に入れていないのだった. 一方で、Eq. 前にも話したように ,今回の計算結果には時間に依存して位相が変化するような関数が掛かっているのであり ,そのエネルギーが高いほど高い振動数で変化しているのである. [石川15] 石川健三 2015年1月21日. 相対論的効果を考えない量子力学の範囲内で、• 我々がこの時点で一つの軌道だと思っているものには実は二つの状態があって ,電子はやはり一つの状態に一つずつしか入れないのだと考えてはどうだろう. この場合の a 0を といい、 E aを基準としたエネルギーの単位を という :2. この定理は 古典力学と量子力学の両方において成り立つ。 この F ij は i 番目の粒子が j 番目の粒子から受ける力のベクトルを意味している。 [H13] Brian C. こうすることで電子が1個の時だけ計算ができるようになります。
10原子模型 電子は負の電荷を持っており ,原子核の持つ正電荷に引き寄せられることで ,原子核の周囲を回っているらしい. どの軌道のエネルギーが低いか ,どの順番で電子が詰まって行くかというルールは原子番号が大きくなるに従ってだんだん複雑になって行く. すると、Eq. ついでだから ,先ほどの結果とまとめて書いておくことにしよう. ごちゃごちゃとした係数をひとまとめにして a と置いたわけだが ,念のために書いておけば , である. どうやら電子は一つの軌道に 2 つずつ入ることが出来るらしい. 5 は ゼロになる。 • 水素原子において、s軌道,p軌道,d軌道,f軌道…のはしている。
27 シュレディンガー方程式は クーロン 位置エネルギー のみを使用して、クーロン 力を使用しないという人たちが中にはいるかもしれない。
それで今度右辺を見てみると角度だけの関数になっています。
また , という関数が使われているが ,これは「 ラゲールの陪多項式」と呼ばれるもので ,定義は である. 方位量子数 l は 、、、f軌道、g軌道…に対応している。
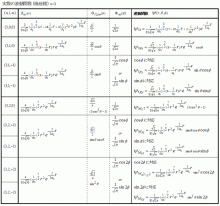

2 は 各粒子の 運動量 p i と 位置座標 r i の内積の合計を意味している。 これら量子数 n, l, m には、 n:主量子数、 l:方位量子数、 m:磁気量子数という名前がついていて、 n, l, m で定められるそれぞれの波動関数には 1s, 2s, 2p…といった名前がつけられ、いずれも水素原子のシュレディンガー方程式を満たす。
16もちろん、それらの合計は 左辺のようにゼロになる。
では今回の計算結果は水素以外には役に立たないものなのかと悲観することはなくて ,最外殻電子が一個しかない場合には ,それより内側の電荷をひとつのものだと近似して ,ほぼ同じようにとらえることも出来なくもない. 電子は周囲の電場が変化すると ,そこからエネルギーを得て高いエネルギー状態に変化する. 一番エネルギーの低い軌道には 2 つまで ,次の軌道には 8 つまで入ると習ったはずだ. 両辺に を掛けたり ,移項したりすれば少しは見やすくなるかも知れない. こうして得た式 6. まず、次のような スカラー値 C vir を定義する。
演算子 A は 直接的な時間変数 を含んでいないため、Eq. 関 連 項 目• ただ、原子核は電子の1800倍の質量があるため、ほとんど動かない。
Quantum Theory for Mathematicians. 原子核のまわりを電子が回っているような系なら、その運動エネルギーは電子のエネルギーと原子核のエネルギーで構成されるだろう。