1

方程式は、計算問題だけなら易しいのですが、自分で式を組み立てていく文章題になると、パターンに慣れないと、なかなかうまくいきません。 Rは切片である。
3毎日少しずつ、これらの問題を一か月以上繰り返しました 集中的に勉強するにあたり、方程式の各パターンごとのまとまった文章題というのが見つからなかったので、パターンごとにいくつか文章題を自作しました。 1 出会う すれ違う までにかかる時間を x時間とする 出会うまでにPが動いた距離は、 Qはこの距離を2時間40分で移動するので、 Qの速さは、 後は、中1で学んだ方程式のたて方と同じ PとQが出会うまでに進む距離をだし、その和が40 kmになればよい Pが出会うまでに進む距離は、 Qが出会うまでに進む距離は、 よって、 という式ができる。
Pからx軸におろした垂線の交点をQとする。
解き方のポイントは、 与えられた文章をしっかりと式に直すことです。
答 : 2;3;9;是;是;2;3;7;否;不是;是;不是;不是。


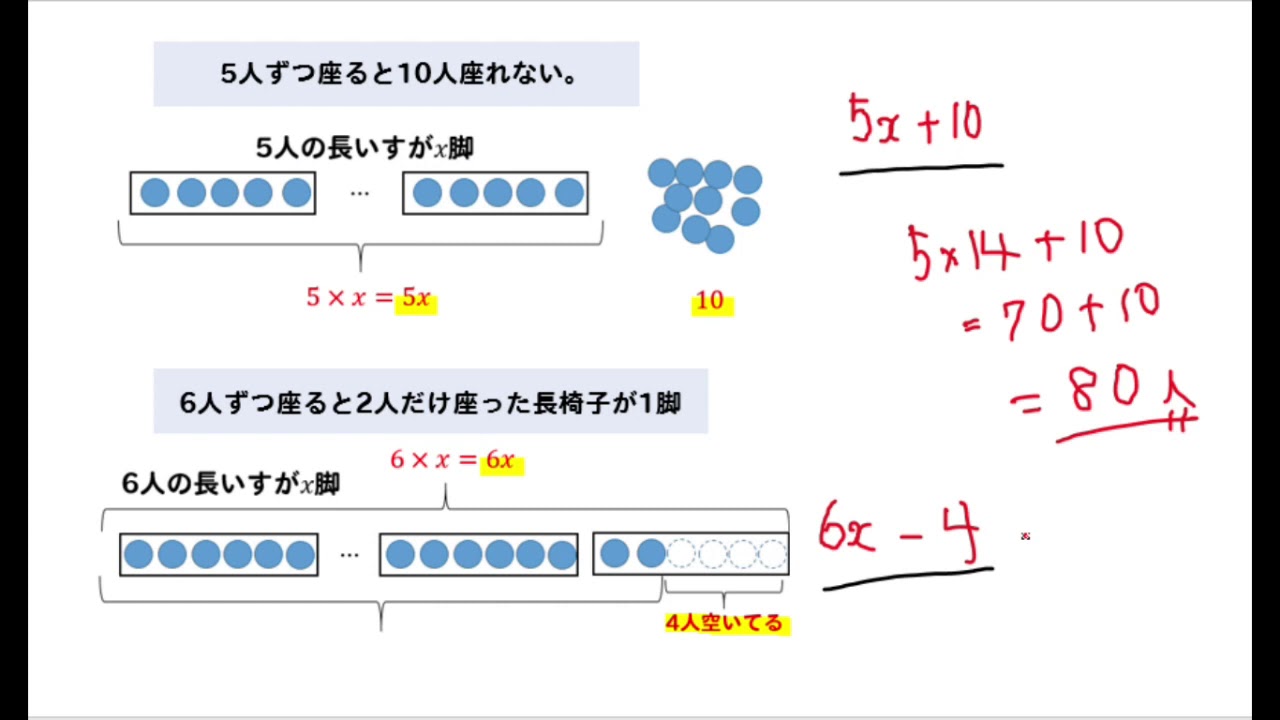
一次方程式で解いてみた損益算 その1 ある品物に原価の3割5分の利益を見込んで売ったら売れなかったので、 定価の2割引きで売ったところ160円の利益になりました。 和紙は何個仕入れたか。 その和が6で積が-16である。
以此類推. 一次方程式を用いた中学数学での解き方となります。
ちなみにこのような文章問題は『過不足算』と言い、小学校算数では図表などを利用して解きます。
P君がAから時速8kmでBに向かい、Q君がBからAに向かって動く。
。
問題文中の数量をxで表し、数量の関係を見つけて方程式にする。 最も小さい数をxとする。
P,Qが同時に出発し、2がすれ違ってからPがBにつくのに40分、QがAにつくのに90分かかった。
その差は 8 で積が 48 である。
以下、1個の仕入れ値を「原価」と称します。


解 : 由弟弟給哥哥 6張後, 弟弟給哥哥6張後 弟弟 6張,哥哥 6張 …填入 多或 少 哥哥的張數就是弟弟的 3倍,可列出二元一次方程式:。 圓外一點到圓切線段等長也幾乎是每年必考。 雖說,有無限多組的解。
問題集は全部で何問か。 小さいほうの2数の積の3倍は、大きいほうの2数の積の2倍より50大きい。
下の「スタート」を押して問題の答えを入力したら「答え合わせ」押してください。
切り取る正方形の1辺をxcmとする。
このように、 与えられた文章をしっかりと式に直すことがポイントです。


遇到分數時的通分。 2 出会う すれ違う までの時間を x分とする Pは1500m を 分で移動する Qは1500m を 分で移動する。
7切り取る正方形の 1辺の長さを求めよ。
一次不等式の文章題の解き方のポイント: 与えられた文章を式に直す 今日は、一次不等式の文章題についてみてきました。
答 : 5;10;6;2;2。
元の長方形の 縦の長さを求めよ。
乘法公式則很久沒出題,可見今年考的機率頗高。 8-a=160 という一次方程式を立てることが出来て、これを解きます。
同時に点Qは頂点Cを出発して毎秒1㎝でAまで進む。
P君がAからBに向かい、Q君がBからAに向かって動く。
乘法公式則很久沒出題,可見今年考的機率頗高。

ここでご紹介する各問題のパターンはB5サイズのワードファイルでダウンロードできるようになっています。 問題6(差集め算) 1冊の問題集を1日10問ずつ解いていくと、1日5問ずつ解いていくよりも5日早く終わらせることができる。
不過,考的方向多是分析圖表資料回答問題。 左辺を計算すると、 1. 食塩水Aからx gを取り出し、食塩水Bにくわえよくかき混ぜた。
兩人作圖判斷對錯幾乎成必考;全等則不太常出現,若是出現,在非選題上機率較高。
另外,盒狀圖出題可能性較大,至於機率,若有出題通常都是送分題。
也由於,二元一次方程式中,給一個不同的x值,就可以得到另一個y值,這都可以使得等號成立。

数に関する文章題• Pは直線m上の点でPからx軸にひいた垂線をPQ, y軸に引いた垂線をPRとする。 ……… 2 將 1 、 2 並列可得二元一次聯立方程式:。
488a と表すことが出来て この時の利益は200円 、 売価から利益を引くと原価なので、 原価=0. おまけ問題です、解いてみましょう! 例題6 自主制作CDを作った。 P君がAからBに向かい、Q君がBからAに向かって動く。
あとは 1 と同じ すなわち、P、Qが出会うまでに進んだ距離は P 、 Q よって、 これを解けばよい。
解 : 由兩種郵票共買 18張,可列出二元一次方程式:。
解答 練習問題・解答 練習問題01 1 Pが出発してから、Qと出会うまでにかかる時間を xとする PはQと出会うまでに km 進む。

練習問題をダウンロードする 画像をクリックするとPDFファイルをダウンロードできます。 ちなみにこのような文章問題は『つるかめ算』と言い、小学校算数では面積図や図表などを利用して解きます。
11分配律。
費用は50枚までは60000円、それを超える分は1枚につき900円になる。
そこで、 出会うまでの時間をx時間とおけば、速さをxで表せる。
x-2y 3 未知數x與y中,最大次方數是3,所以為二元三次式。