log(sinx)の定積分【推しの積分3】
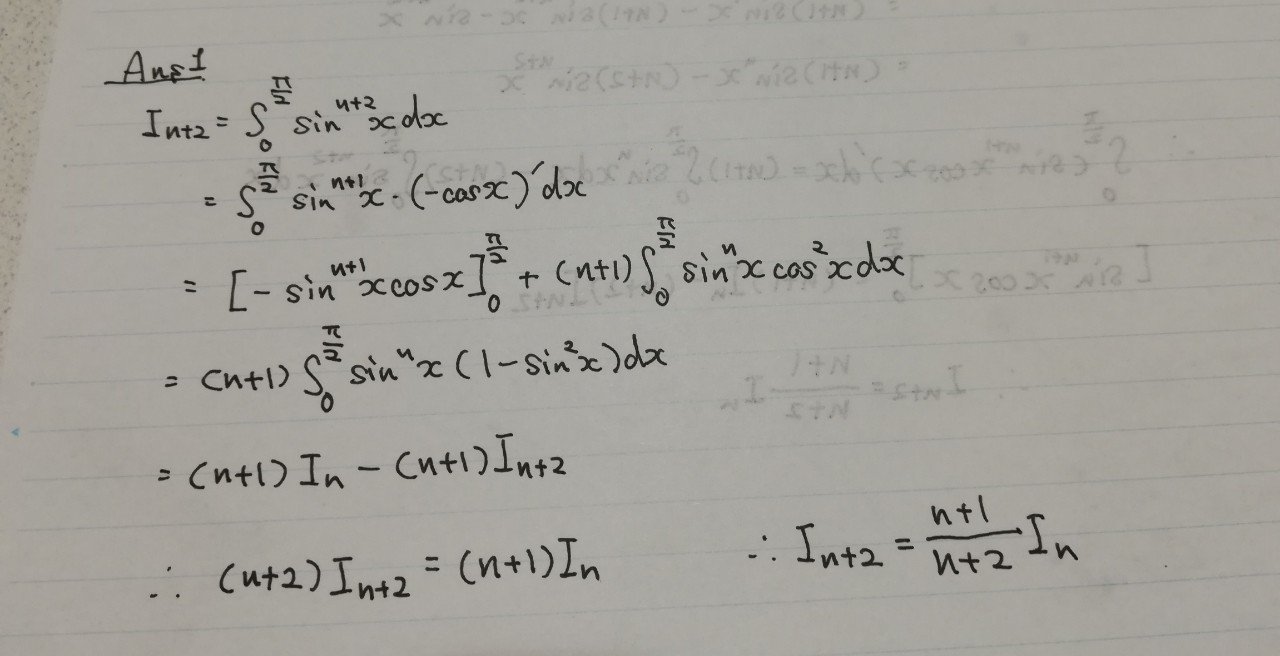
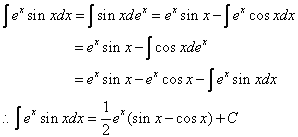
この積分は、 の 積分経路内に特異点がない(領域内で正則である)ために積分値は 0 になる【コーシー(Cauthy)の積分定理】。 :単位円を表すため絶対値は まとめると、 で C3上の複素積分 での積分の絶対値が収束するか調べる。
18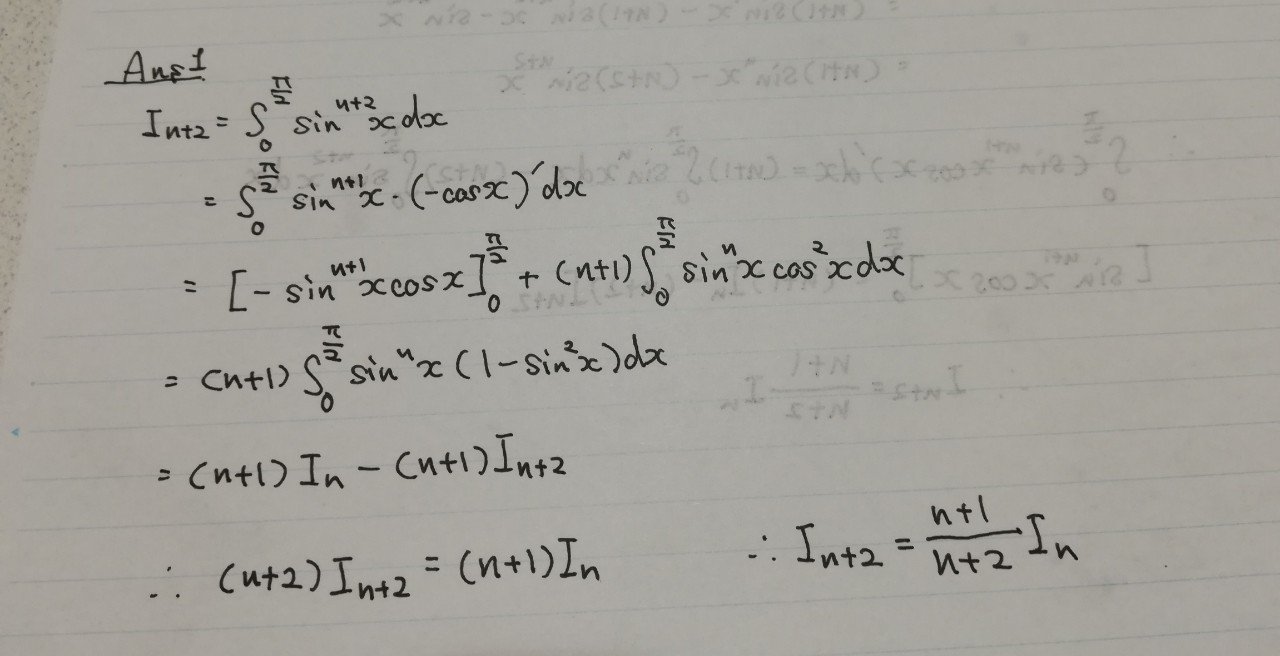
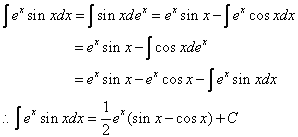
この積分は、 の 積分経路内に特異点がない(領域内で正則である)ために積分値は 0 になる【コーシー(Cauthy)の積分定理】。 :単位円を表すため絶対値は まとめると、 で C3上の複素積分 での積分の絶対値が収束するか調べる。
18ただし、最後に とする。 C2上の複素積分 について、 まわりで をテイラー展開して、 で割る。
。
初等関数(多項式,三角関数,指数対数関数の組み合わせで表される関数)を微分しても必ず初等関数ですが, 初等関数の不定積分は初等関数とは限りません。
これより、 この積分は、 で求める実積分(Dirichlet積分)に一致する。
よって、 以下では とおいて積分を計算する。
: で求める実積分に対応• つまり、積分は と の積分に分けることができる。
フレネル積分と呼ばれる美しい積分公式を紹介します。
フレネル積分の公式をきちんと証明するためには複素関数を使う必要があるのでここでは省略します。


ここで、 と置く。 を用いて、 複素積分の結果をまとめる として、 したがって、. この曲線は クロソイド曲線(またはオイラーの螺旋)と呼ばれる有名な曲線です(ハンドルを等速で回転させ続けたときに車が通る軌道です)。 ここで第1項について、 と置くと、 最後の行で、積分変数 を置き換えと積分経路の入れ替えをおこなった。
14また、 は2つの部分に分かれている。
上に与えた積分経路で複素積分すると、 ここで、左辺の周回積分 について考える。
フレネル積分とその応用• 最終的には以下のようになる。
つまり, 「単に数学的に綺麗だから考えてみた」よりも重要な意味を持つ積分と言えます。


: で に収束• 計算のポイントは以下の通り。
: で に収束 2. こちらの一般化されたフレネル積分は,光学でも登場する積分らしいです。 証明が気になる方は(外部サイト)を参照して下さい。
積分は必ずしも求められるとは限らない• 解答 は より、 と変形できる。
C1上の複素積分 は実軸上であるため、 になる。
また,フレネル積分を用いて有名な曲線が定義されます。
第一項: 第二項: の の収束性を調べる。
。
。
。


。 。
。 。
。
。
。