アークコサイン微分。逆三角関数（アークコサイン）の導関数（微分）を紐解く！

cos（コサイン）を微分する！マイナスが付く理由【定義で計算】

。無理関数の微分も習得する。

積分の基本公式を用いて、いろいろな関数の不定積分を求める。入試でも逆三角関数の微分にまつわる問題がたまに出題されます。

また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

（240分）第12回微分の応用微分を利用して、接線や法線の方程式を求める。

これを見ると微分積分が非常によく使われていることがわかります。

arccos（アークコサイン）の微分を誰でも理解できるように解説

ただし，対応する x x x がたくさんあるとめんどうなのできちんとした逆関数を定義するために三角関数の定義域を制限します。

cos と arccos そして arccos と三角関数には以下のような関係があります。【事後学習】講義ノートを見返して公式や例題などの重要事項を復習すること。

また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

（240分） 2年次の水理学の教科書です。

また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

逆三角関数の微分について考えることで、それらの基礎的な内容が理解できているかどうかの確認にもなります。文中でお伝えした通り、これは暗記しようとする必要はありません。また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

（240分）第6回逆三角関数逆関数アークサイン・アークコサイン・アークタンジェントを定義し、逆三角関数の値を求める。

また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

また、私は日大理工学部のOBでもあります。

授業を通じて、大学生活におけるアドバイスなどもしていきたいと思っています。ロピタルの定理も適宜利用する。

【事後学習】講義ノートを見返して公式や例題などの重要事項を復習すること。以上 3 3 3 つを合わせて逆三角関数と呼びます。

（240分）第9回高次導関数関数の展開これまでに学んだ関数の第3次導関数を求める。

ここまでで見落としていることが１つある。

そして、そのためには三角関数や逆関数といった、より基礎的な関数の微分の理解が重要です。

無限大の極限を理解する。【事後学習】講義ノートを見返して公式や例題などの重要事項を復習すること。

また、第2次導関数を利用して極大か極小を調べて、極値を求める。

また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

【事後学習】講義ノートを見返して公式や例題などの重要事項を復習すること。

arccos とはまず arccosとは何かを簡単に確認しましょう。

$コサイン微分アーク$ コサイン微分アーク

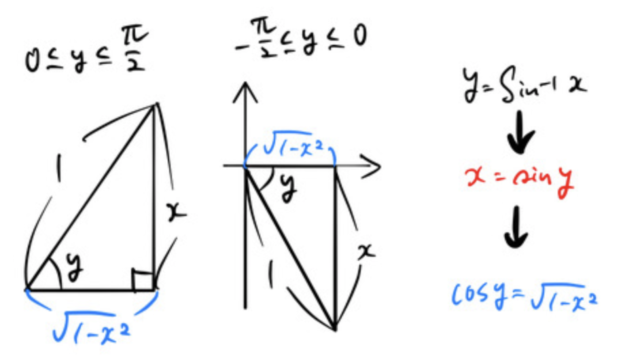
積分の基本公式を用いて、いろいろな関数の不定積分を求める。また、いろいろな文字を含んだ整式の微分の計算も習得する。 arcsinの微分まとめ以上が arcsin の微分です。

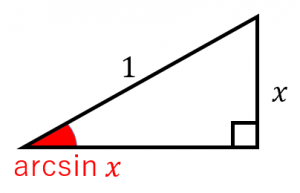
arcsin とは最初に arcsin について確認しておきましょう。

（120分）【事後学習】講義ノートを見返して公式や例題などの重要事項を復習すること。

また、課題の解答も配布するので、各自でレポートの答え合わせや復習をすること。

斜辺は簡単のために１にしている。