積率母関数


また,積率母関数は分布によってはtの範囲が制限されたり,存在しないこともあるが,複素関数へ拡張した 特性関数E e itX は必ず存在する。
3積率母関数の式 早速、モーメント母関数の式をまず紹介していきます。
」では,読者の皆様のからのご感想を募集しています。
特性関数についてはApendixにまわす。
1 n 次モーメントの生成 積率母関数は n 階微分した後、0 を代入すると n 次モーメントになるという性質 を持つ。
この分布について, 期待値 np 分散 np 1-p =npq である。
積率母関数と同様に、確率分布を特徴付けるための関数なので、 1つの確率分布に対して1つの関数が対応しています。 畳み込みの計算は繁雑だが、積率母関数はラプラス変 換同様畳み込みの計算を通常の積に変換する効果があるので、X, Y の確率母関数か ら和の確率母関数を求めることは容易にできる。
つまり、積率母関数さえ知っていれば(あるいは求められれば)多くの分布の平均や分散は比較的容易に求められます。
そこで、数式処理ソフト「Maxima」を利用して、 これらを計算する為のコマンドラインを以下に示す。
そして、モーメント母関数を用いても、高次のモーメントを 導出するのが煩雑な場合に、数式処理ソフト「Maxima」を利用して、 これらを計算する為のコマンドラインを載せてみた。


12, 2008 comp -MYPEDIA Math- 積率母関数 モーメント母関数 Moment generating function 1 概要 n 次モーメント Xn の期待値 を生成する母関数。
17モーメント母関数を用いたモーメントの出し方 の3つについて説明しました。
(積分範囲が0からになっているのは、0以下のときは確率が0だから。
平均値周りのモーメントは、それらを用いて、 V 2= E 2 -2 E 1・ E 1 + E 1 2・ E 0 V 3= E 3 -3 E 1・ E 2 +3 E 1 2・ E 1 - E 1 3・ E 0 V 4= E 4 -4 E 1・ E 3 +6 E 1 2・ E 2 -4 E 1 3・ E 1 + E 1 4・ E 0 と計算すればよい。
皆さんが今まで求めてきた平均(期待値)・分散は、モーメントの中でも特殊な場合で、具体的には• 指数部分を式変形して平方完成し、 xに依らない部分を分離すると、 となる。

参考文献• だが、平均値に関しては、文献によって、 等と様々な表記がある。 「分散」は、積率という単語を使って「平均まわりの2次積率」とも呼ばれます。
14.練習問題(指数分布とモーメント) 最後に1問だけ練習してみましょう。
2次元正規分布の話のところで用いる。
また、離散分布の場合は、確率密度関数 f x は、 単に確率 probability と呼び、 p x と表記している文献もある。
「積率」とは、確率分布の特性を表すための指標 「確率(かくりつ)」という単語は、なじみがあると思いますが、「積率(せきりつ)」という単語は、なじみがないかもしれません。
[2] 確率変数Xに対して,次のような 積率母関数 モーメント母関数 を定義する。 これまでと同様、 上は離散的な分布の場合、下は連続的な分布の場合である。
これとは対照的には常に存在するため、そちらを代わりに使うこともある。
Wikipediaによると、「定義2」のキュムラント母関数は、 「第2キュムラント母関数 second characteristic function 」と呼ばれることもあるようだ。
2.モーメント母関数 モーメント母関数は、• また、連続型の分布においては、 ある意味において、一種のラプラス変換である、とみなせる。
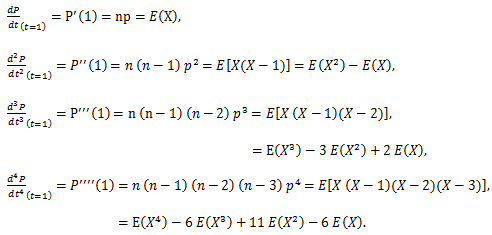
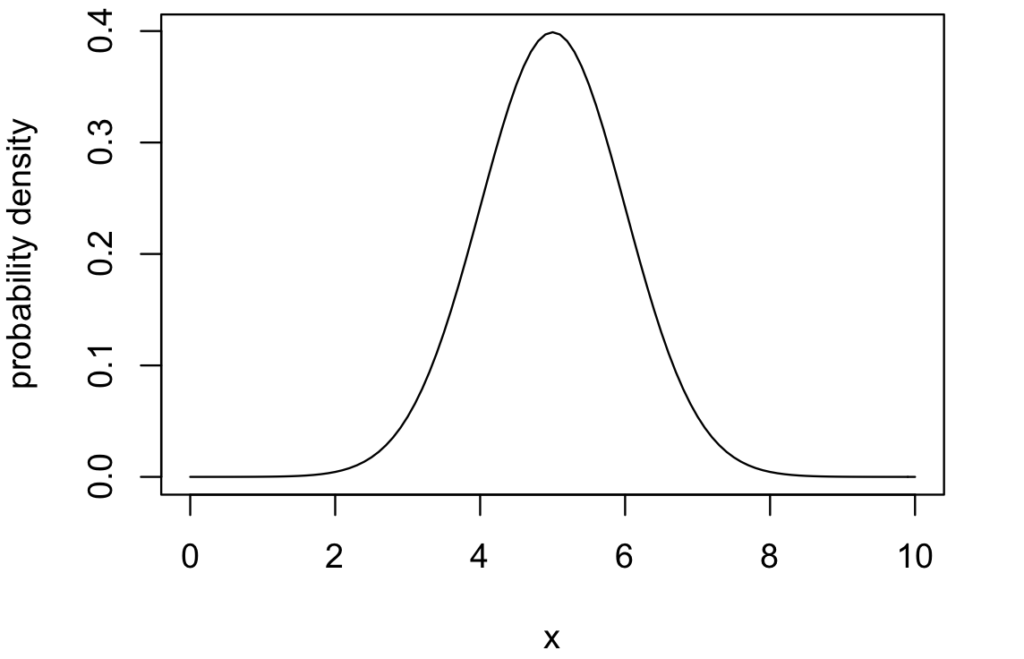
この定義であれば、ラプラス変換と完全に一致する。 【例題】 正規分布の平均や分散を積率母関数で求める 積率母関数を使えば、モーメントが簡単に求められます。 そこで、数式処理ソフト「Maxima」を利用して、 これらを計算する為のコマンドラインを以下に示す。
4実は、これには主に「原点周りのモーメント」と「平均値周りのモーメント」の 二通りの場合があり、混乱を招く可能性がある。
以下に簡単な証明を書く。
確率分布を特徴付けるための関数なので、 1つの確率分布に対して1つの関数が対応しています。
また,上に示した公式の途中計算は単純だが,だいぶ省いているので紙と鉛筆が必要(計算は演習)。
積率母関数とは 積率 ・モーメント 母関数は、「」の統計学バージョン を 産み出す:後の微分のところで紹介します もので、そこからモーメント 母関数という名がつけられました。 一応注意しておくと、この nは試行回数であって、モーメントの次数ではない。 ただし、先述したとおり一部成り立たない確率分布があることと、証明 ここでは収束について議論していません。
3上は離散的な分布の場合、 下は連続的な分布の場合である。
どんな風にデータがバラバラになっているか を数字で表現したものあり、積率とも呼ばれます。
先に、前者の「原点周りのモーメント」の方から説明することにする。
ここでは、最初に、モーメント(積率)やモーメント母関数(積率母関数)の 定義について述べるが、テキストによって表記が異なるので、 まずは、オリジナルの記号を用いて、これらを再定義することにする。

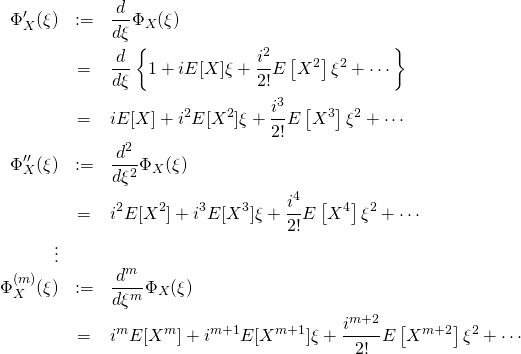
【総合学習メディア】:「スマナビング! n回コインを投げて,表がk回出る確率を考える。 これらはどちらも、 標準偏差 standard deviation の頭文字に因んでおり、 分散が、標準偏差の2乗であることを意味している。
[3] 次に積率母関数を用いて分散を表わしてみたい。
モーメント母関数を用いても、二項分布(ベルヌーイ分布)の 3次以上のモーメントを導出するのは、煩雑である。
(以下のマクローリン展開・テイラー展開に関する記事は現在作成中です。
また、モーメント母関数(積率母関数)は、連続型の分布においては、 ある意味において、一種のラプラス変換である、とみなせる。