意味がわかる主成分分析


課題2: iris. もちろんだけどダミーデータですよっ。


課題2: iris. もちろんだけどダミーデータですよっ。
例えば英語ができる人にはどのような要因が考えられますか。 ・因子得点の解釈 また因子分析には二種類の方法が存在します。
したがって第1、2固有値に対応する得点のみを分析すれば良いでしょう。
つまり、主成分分析とはこの例を用いると、 『各生徒の得点を教科ごとの相関関係から求めた主成分ごとに合成変数 理系科目や文系科目など を用いて分析する』 という解釈ができます。
次に因子分析をやっていきます。
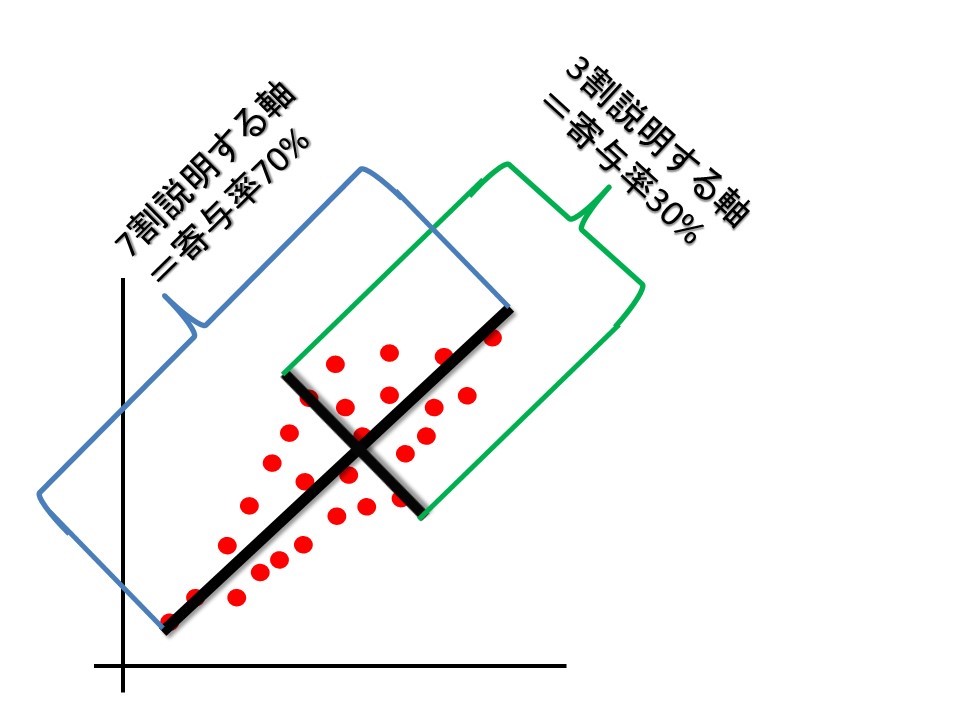
この場合、各データ ここでは算数や国語の点数 の相関関係を見て、 その傾向を主成分としてプロットすると 各データの持っている傾向が読み取れるようになるのではないでしょうか。 この固有ベクトルは長さが1の単位ベクトルであり、互いにすべて直交 =内積を取ると0 しています。
3発展課題4: scikit-learn を使わずに、SIMPLS アルゴリズムによる方法で PLS を行うプログラムを作成せよ。
主成分1:ピッチング能力 打たれにくさ• これならば、線形クラス分類でもそれなりに分類できそうです。
(探索的因子分析)。
まとめ 本日は、Rの因子分析を試してみました。
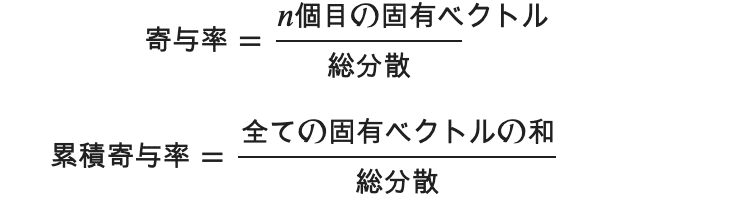
主成分分析や因子分析と異なり、コレスポンデンス分析の出力は、負荷量と得点という組み合わせではなく、行得点と列得点という得点同士の出力である。 この際、setosa と versicolor とを合わせたものを1つのクラス、virginica をもう一つのクラスとして、2クラス分類をすること。
13平均を引くことで、射影した際に主成分軸での原点は0になります。 また一番したのコードを実行することでfit関数とtransform関数を同時に実行することができます。
PC:Principal Component 主成分 軸のことかと。
説明変数も目的変数もオートスケーリングを行うこと。
・ 共通因子:分析対象となる変数の組に共通する因子のこと 例:英語と数学の場合、考えられる共通因子は読解力・論理的思考力など ・ 独自因子:各変数に独自に関わる因子のこと。
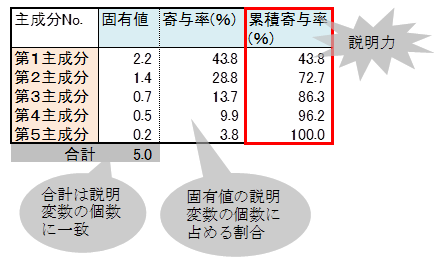
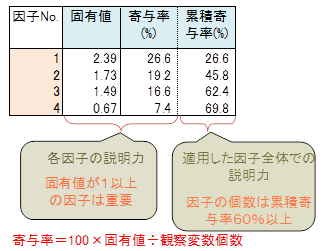
(カイザーガットマン基準) (引用:誰も教えてくれなかった因子分析より) 固有値は、観測変数、つまり、質問項目の数と同じだけ算出されます。
主成分分析の役割 ・データの特徴抽出 ・データの次元節約 ・多次元特徴量の可視化 では主成分分析に深く入っていく前に軽く流れを紹介します。
目的が差異の発見ではなく,データを圧縮して関係性を見る場合には主成分分析,類似関係や差異を見つけることが目的であるならコレスポンデンス分析というように,一般的には分類できる。
show 3品種を区別するだけの目的なら、第2主成分までで何とかなりそうです。
このプログラミングのトレーニングを経て、中級者に一気に近づくことでしょう。 分散共分散行列ではなくて、相関行列を求めても同じになります。 そして k の値を変えながら、AD の内側と外側とでテストデータの r2, RMSE, MAE を計算して比較し、考察せよ。
7さらに、トレーニングデータとテストデータそれぞれにおいて、実測値と計算値もしくは予測値との間で r2, RMSE Root-Mean-Square Error , MAE Mean Absolute Error を計算し、実測値と計算値もしくは予測値とのプロットを作成せよ。 import math import numpy as np import matplotlib. factor0で比較するなら大き方がより文系科目の点数が良いことも読み取れます。
また説明変数も目的変数もオートスケーリングを行うこと。
最後に 因子得点を求めていきます。
縦軸が固有値、横軸が因子の数を意味します。

PC1 横軸 に着目すると、右の方が奪三振率が高いのはわかりますが、 防御率や被安打率、WHIPに関しては低いほうが良いので 奪三振率、防御率、被安打率、WHIPは横軸の右に行くほど優秀となります。 PCAの欠点 PCAの欠点として、 プロットした2つの軸の解釈が難しいことが挙げられます。 課題6: iris. k最近傍法 k-nearest neighbor, kNN によりモデルの適用範囲 Applicability Domain, AD を設定せよ。
10第k主成分は第k固有値に対応する(長さ1の)固有ベクトルとして求める事が出来る。
最初の方の課題ではこちらを使用します。
主成分分析は教師なし学習なので、正解(ラベルや教師データ)がないため、分散によって次元の重要度を決めます。
頑張ってください。