重ね合わせの原理 (電気回路)
でもそれは間違っていた。 まとめ 今回は重ね合わせの原理の意味を説明しました。 5 という値が付けられる。
17では、「未決定状態」とは、何か? 次の二通りだ。 右向きの運動量と、左向きの運動量は複素数で示した波動関数から計算される値と正確に一致している。
[ コマ数] コマ数(露光回数)を設定します。
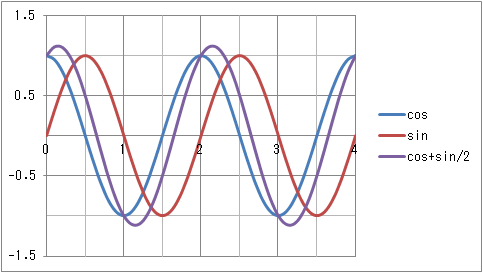
定常波は,同位相で波長,振幅,速さが等しい2つの波が互いに干渉してで きる。
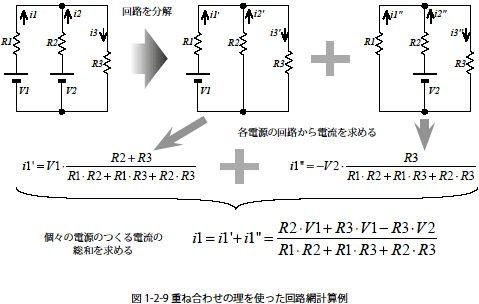
線形系は数学的に解析が容易だという点で重要性が高く、やのようなへの、理論など、多数の数学的技法が適用可能である。
この状態で粒子の運動量の測定を行うと、右向きの値が検出される場合と、左向きの値が検出される場合があり、その確率は半々となることは直感的に理解できると思う。
x、y、zの直交座標系を考えよう。
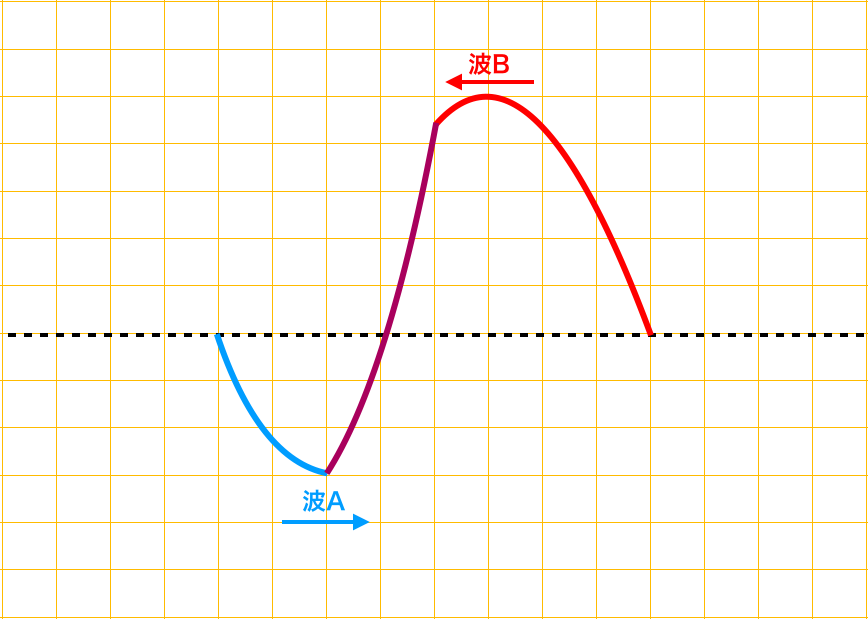
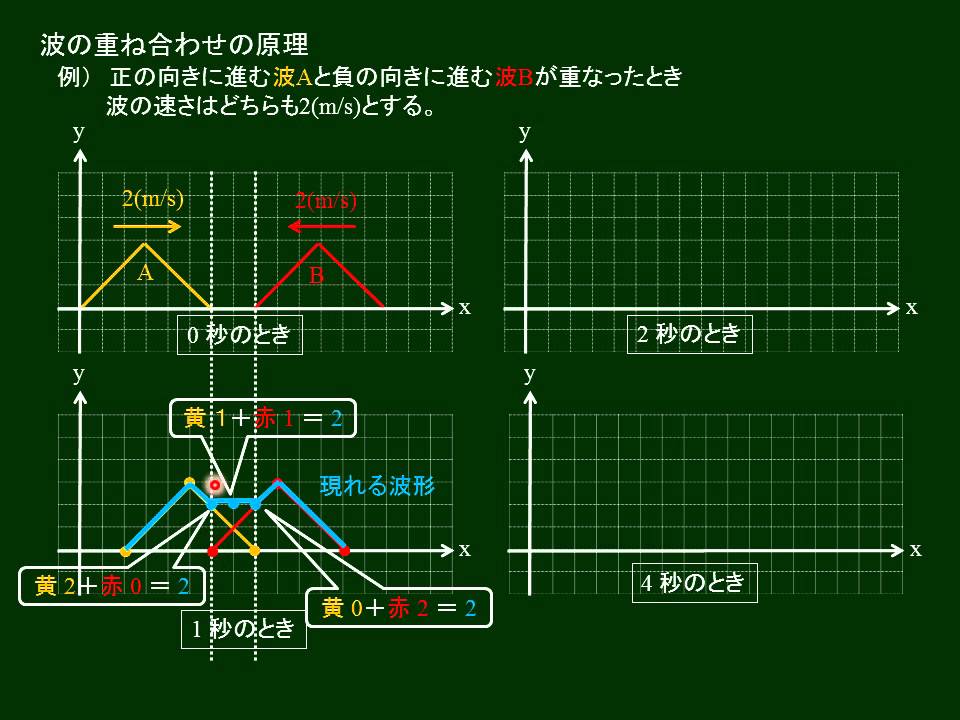
比例関係のとき、C点の変位は、1つ毎の荷重に対する変位の総和を合計すれば良いです。
これがホイヘンスの原理の不完全な点である。
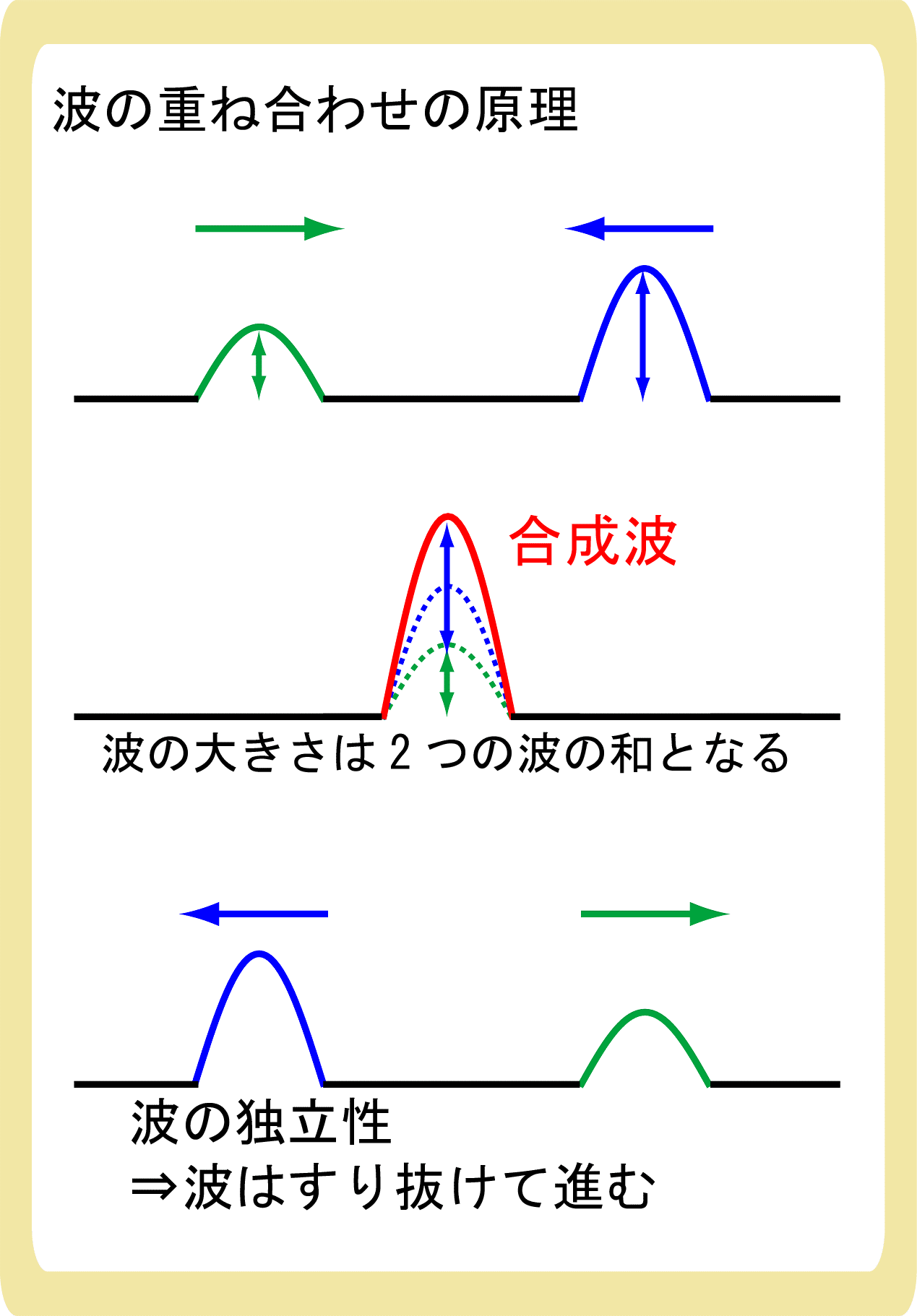
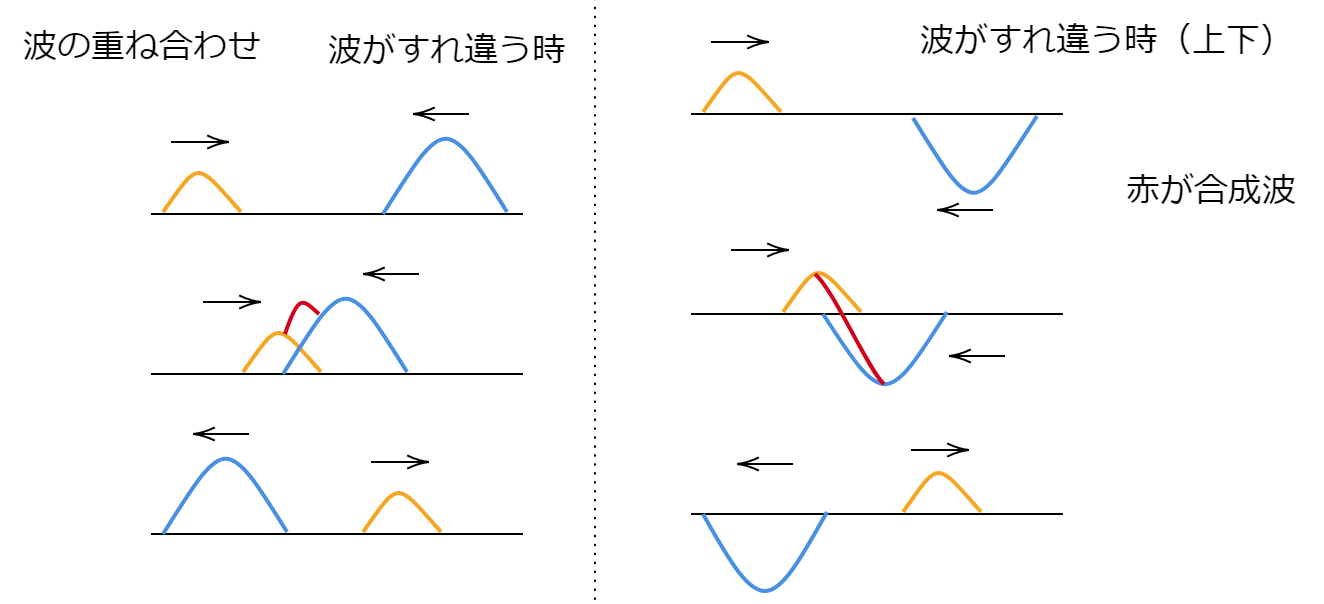
他方で ()などでは合成波の振幅が個々の成分より大きくなる。

この式は、眺めた瞬間には馴染みのないものであろう。 二つ以上の入力が同時に与えられた時に系が返す応答が、それぞれの入力が単独に加えられた場合に返される応答の総和となることをいう。 モデルとは、自然の基本原理である。
14右図はウエーブマシンでの位相変化を図示したものである。
4 の重みが付けられている、というふうになることもある。
図にマウスを置くと動画になります 回折 diffraction 平面波がスリットの下から上に向かう場合,波の波長がスリット幅より長いと,直線だった波面がスリットを通過するときに,素元波からの包絡面が円形になり,スリットを通過した後は波面が円形波に変わる。
このことは、「超球理論」における「玉突きモデル」で説明される。
次の時間間隔で半径SS 1とする素元波が波面Sから連続して作られると,波の前方包絡面S 1が作られるともに後方の包絡面S 2が作られることになるが,現実にはS 2の波面 逆行波 はできない。
……それが現代の物理学者の主流である。
もし、演算子を作用させて、ある関数が定数の解をもたらすなら、その関数は演算子に対する固有関数であるといい、求められた値を固有値と呼ぶ。
いかなる物理系においても、ある時刻における波形(変位の空間分布)は、波源(波動に影響を与える外力など)の条件および(初めの波形)のもとで微分方程式を解いて求められる。

これは、波動関数の満たすべき条件に反しているにもかかわらず、この場合には許されている。 つまり、「生きている状態」および「死んでいる状態」が、どちらも実際に成立している。
2非線形系の既知の解からのずれをによって解析しているときにも重ね合わせの原理が適用できる。 歴史 [ ] によると 、重ね合わせの原理(「振動系の運動は、一般に系の固有振動の重ね合わせで与えられる」)を1753年に初めて提唱したのはであった。
Ch、または Qの静音連続撮影に設定しているときにシャッターボタンを全押しし続けると、多重露出で設定された撮影コマ数まで撮影し、合成画像を保存します。
……これがつまりは、前の文書に当たる「」で示したことだ。
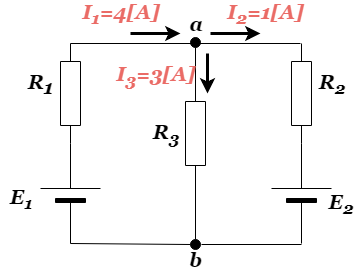
重ね合わせの原理とたわみ 重ね合わせの原理を使えば、2つ以上の荷重が作用する梁のたわみも簡単に計算できます。

かさね色目 >>>かさね色目 有職の「かさね色目」 かさね色目には3種類の意味があります。
下図で境界面の上下で波の速さが異なるので,AA'<BB'となるため屈折が起こる。 猫は、半分ぐらい「生きているらしく」、かつ、半分ぐらい「死んでいるらしい」 現実世界では、次のようになるはずだ。
スリットAを通る経路を赤線で示し、スリットBを通る経路を青線で示す。
猫の生死の値が 0. メニューガイド• 1644年 デカルトが論文「光学」で確認している。
(後者の例では、二つの場所は二つのスリットに相当する。

。
固定端は,音波が固体,液体に反射する場合や弦が固定されている端点で反射する場合,光の場合屈折率の小さな物質から屈折率の大きな物質への反射 例えば空気から水への反射 などである。
Foundations of Physics 23 2 : 185—195. 一方、片方に多くの重みをつけることもある。
) なお、重ね合わせの解釈では、次のような説明も考えられる。
だから、いちいち「重ね合わせ」なんていう概念を使うべきではないのだ。
誤解しないこと。 量子について、「波でもあり粒子でもある」とか、「二つの場所に同時に存在する」とか、「二つの経路を同時にたどる」とか、「猫は生きていて、かつ、死んでいる」とか、そういう表現もある。
このアニメーションのように二つの波が等しい波長・振幅を持っていた場合、が作られる。
一方で、干渉と回折という概念が不分明なのは 波面の分割と 振幅の分割の区別が意識されていないためだ、という主張も存在する。
採用しているモデルのなかに、「回転中」という状態が見出されないのだ。