【EXCEL】分散(VAR.P,VAR.S,VAR…)の求め方の違いを例題を使って理解する
:平均を計算するセルの範囲• エクセルでは、 QUARTILE関数で各四分位数を求めることができます。
14
:平均を計算するセルの範囲• エクセルでは、 QUARTILE関数で各四分位数を求めることができます。
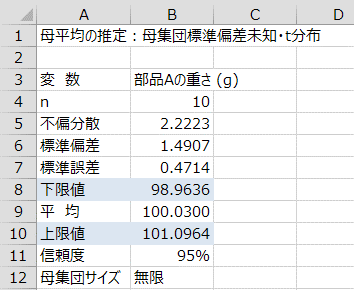
14, p. まとめ ここでは標準誤差(SE)の定義や標準偏差との違い、エクセルにて標準誤差を計算する方法について確認しました。
それ以外の関数は数値のみしか扱えません。
検定統計量を求める 5 で触れた不偏分散をあらためて正しく計算しなおします。
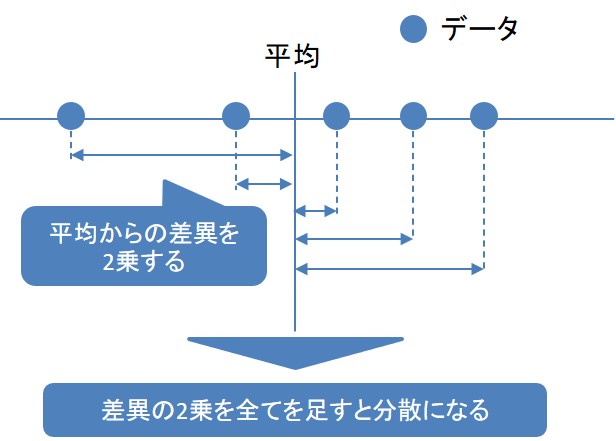
このように「分散」を求めることで「データのばらつき具合」を比較する方法もある。
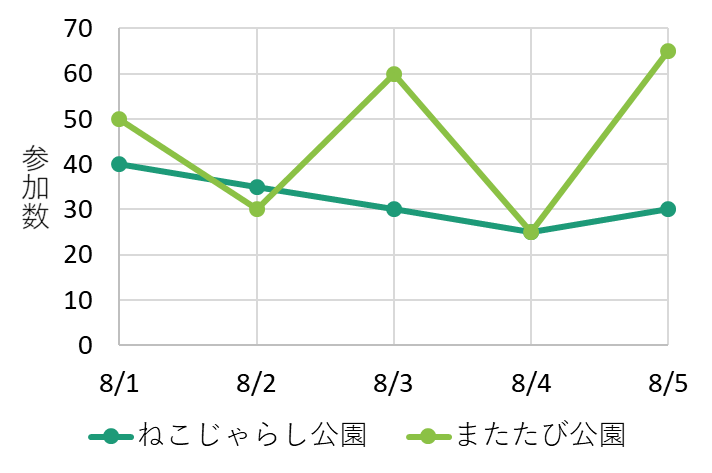
これらの値は,下図の淡いピンク色の領域で示されます 赤いハッチングの領域[有意水準]と重なる部分あり。 後者では交互作用が重要になります。 算術平均は、 AVERAGE関数を利用します。
このように平均では同じであっても、複数データのときは、水準の組合せによるばらつきにより、交互作用が認められることがあり、それを考慮すると、有意差が明確になることがあるのです。
P の入力 もちろん、この結果は、先ほど手計算したものと同じ数値になる。
例えば作業者A,B,Cが機械P,Qを使用して製品を生産しているとします。
「東京」の「差の2乗」の合計 「大阪支社」のデータについても同様の処理を行うと、以下の図のような結果が得られる。
「差の2乗」を求める数式(東京) この数式をオートフィルでコピーし、その合計を求めると、以下の図に示したような結果が得られる。 結果として、分散比=3. 50であり、他の値と比較して小さいことからも想像されます。
では「VAR. :平均を計算するセルの範囲• ここから本ページの本題。
分散とは データ全体のばらつきを表す数値です。
PLEASE CHOOSE A METHOD• Sで置き換えられました。
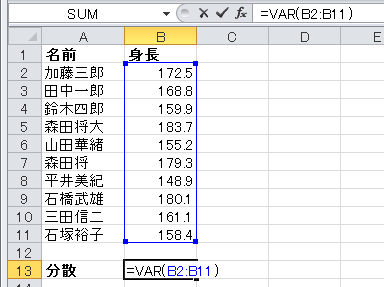
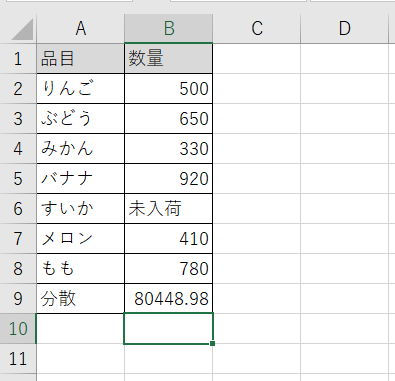
補足 VAR関数は、 2010で VAR. 標準偏差をエクセルで出すには、標本調査の場合は STDEV. 「差の2乗」を求める数式(大阪)• 統計学の分野では、このような手順で求めた数値を「分散」と呼び、「データのばらつき具合」を示す主要な指標の一つとして利用されている。
2因子数が1のときを 一元配置分散分析、因子数が2のときを 二元配置分散分析といいます(3以上のときを多元配置分散分析といいますが、複雑ですので省略します)。 それぞれの関数の特徴を簡単に説明します。
2 の場合に利用 は,それぞれ次式で求めます。
「数値2」・・・分散を求める、または、の範囲を指定します。
net• つまり帰無仮説が棄却されれば,店側のアナウンスの裏付けが弱くなります。

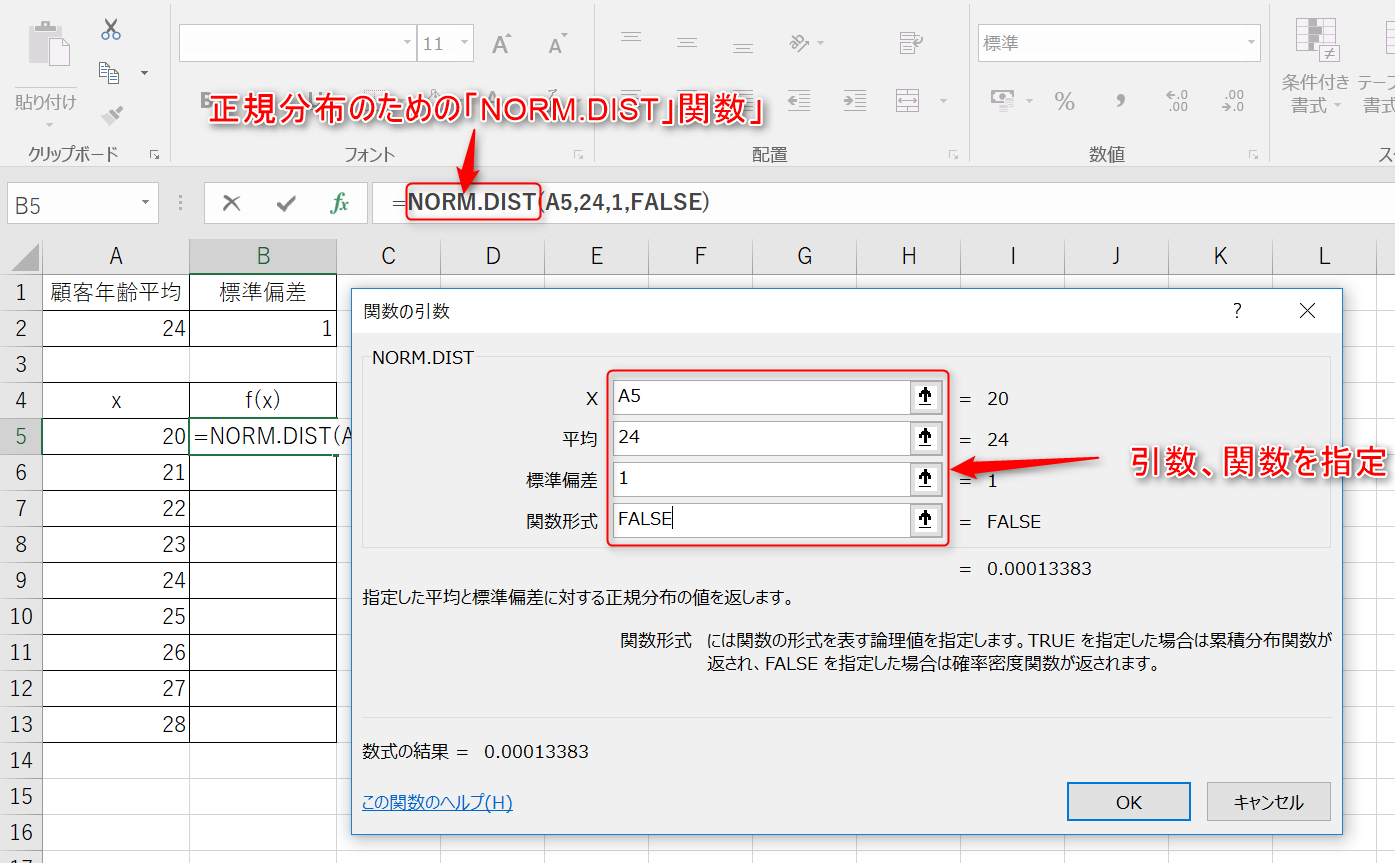
また、ここでは、そのテータ個数がすべて同じ(数値例では5)とします。 新人研修は「東京本社」と「大阪支社」の2カ所で行われ、それぞれ20人の新人を対象に研修&テストが実施された。
13070(P-値)ならば棄却できることを示しています。 Excelでの用語は、本文での用語と異なるものがあります。
というのも、Excelには「分散」を求める関数が用意されているからだ。
ついでに、もう一つの方も関数を使用して出してみると、約10. 調和平均は、 HARMEAN関数を利用します。
分散の求め方 次に本社と大阪支店の分散を求めます。
REFERENCES• 分散とは、複数のデータがある時に、それらのデータの平均値とそれぞれのデータのばらつき具合を数値で示したものです。 が大きいと平均値と離れたデータが多く、ばらつきが大きいデータになります。
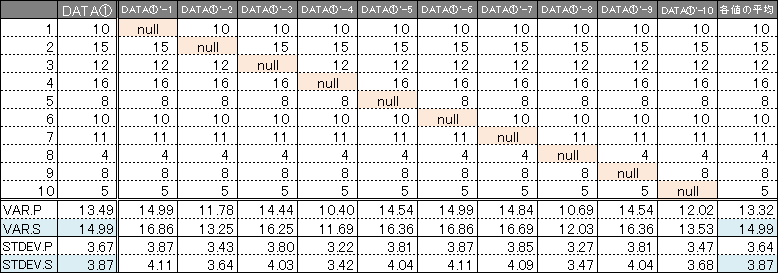
書式 : HARMEAN 数値1, 数値2,. 標準偏差は、10回の実験のバラツキの程度を数値化したものである。
「え?さっきの関数選択の画面にVARPという名前が見当たらなかったけど・・・」 そう。
まとめ 偏差と分散の説明でした。

5」となり、合点がいきますね。 上述の「統計学的な接近」で示した手順で計算すると、次の結果が得られます。
。
S関数」「VAR関数」です。
このような場合、平均と標準偏差をうまく利用して図示化すると、 10本のデータの性質が良く分かるようなグラフを描くことができる。
S関数 互換性を考えるならば、VARP関数を使用した方がよいでしょう。