二等辺三角形の定理。【中２数学】図形の中でも重要なものの１つ、二等辺三角形について徹底解説！

直角二等辺三角形とは？定義や辺の長さの比、面積の求め方

では、そのほかの二等辺三角形の説明は、何なのか？これは、「二等辺三角形とは、２つの辺の長さが等しい三角形」と決めたときに、証明された事柄と考えるといいでしょう。この性質は定理として、証明や計算問題で自由につかうことができるんだ。

よって、右斜辺の長さもaですね。頂角の二等分線を底辺にひく• このとき、三角形の合同条件は以下の4つです。

なのでぜひこれは覚えておきましょう！スポンサーリンク【同人誌】反撃の数学を電子書籍にしました。

数学は「積み上げ学習」と言われており、以前の学年で習った内容をもとに、発展した学習を積み上げていきます。

作図のイメージと合わせて、3つの合同条件を確認しましょう。

二等辺三角形の角度は？1分でわかる求め方（計算）、辺の長さとの関係、証明

二等辺三角形と直角三角形の両方の性質を理解していないと問題を解けないケースが多いです。

意味、計算方法が理解頂けたと思います。角度によって定義された三角形・直角三角形…１つの角が直角である三角形・鋭角三角形…３つの角がすべて鋭角である三角形・鈍角三角形…１つの角が鈍角である三角形三角定規に代表される直角三角形。

直角三角形だけ利用できる合同条件があるため、覚えるようにしましょう。

定義であるため、以下の二等辺三角形では必ずAB＝ACとなります。

二等辺三角形の底辺の長さの求め方って知ってる？？ふつうに生きるためなら求め方知らなくても大丈夫。

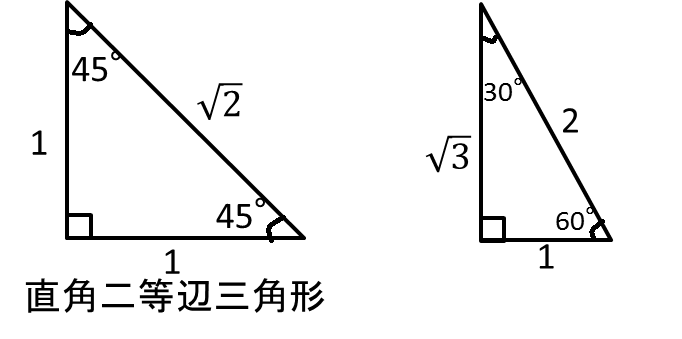
二等辺三角形の底角が等しい証明なお、なぜ二等辺三角形であれば底角が等しいのでしょうか。左鋭角が45度のとき、右側の角度も45度です。特殊な二等辺三角形に、直角二等辺三角形や正三角形があります。

以下のように、形が異なるケースがあるからです。

…続きを読む. 数学の問題で二等辺三角形が出題されている場合、2つの辺については同じ長さとみなして問題を解くようにしましょう。

次の手順で底辺の長さが2㎝、等しい辺の長さが3㎝の二等辺三角形を作図します。

頂角が90度です。

シムソンの定理. あとで平行軸の定理を使うために、自分で勝手に軸を設定しましょう。

こういった理由から二等辺三角形の定理は「間違いなくそうだね！」と言えるわけです。

数学で重要な図形なので、定義や性質、合同条件を覚えたうえで問題を解きましょう。

斜辺と他の辺がそれぞれ等しい三角形の合同条件は全部で5つです。

定規とコンパスを使って底辺をかき、分度器で両端の角を決めて定規で結べば、三角形をかけます。

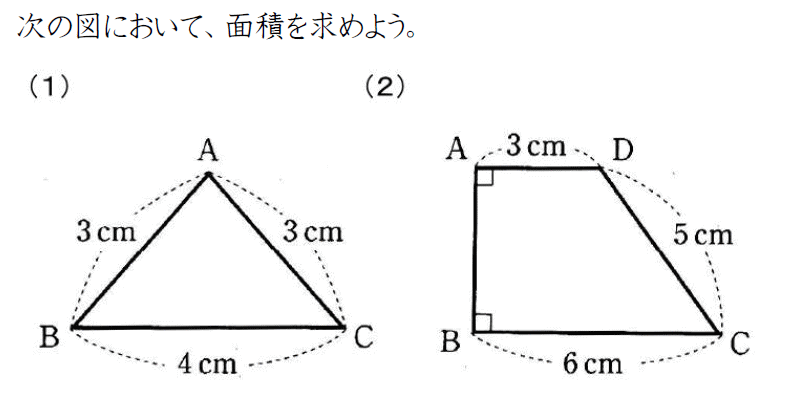
つまり、正三角形は、二等辺三角形でもあります。例えば、頂角が90度のとき２つの低角は45度です。 3．また， B C BC BC の中点を M M M とおくと三角形 D B M DBM D BM と D C M DCM D CM は合同（二辺とその間の角がそれぞれ等しい）。

もくじ• つぶれたイメージの鈍角三角形。

よって底辺の長さはです。

軸がどの方向になるかをしっかりと理解しておきましょう。

練習問題：図形の証明問題 Q1. 点Bから辺ACに対して、垂直な線BDを引きます。

$定理の二三角形等辺$ 定理の二三角形等辺

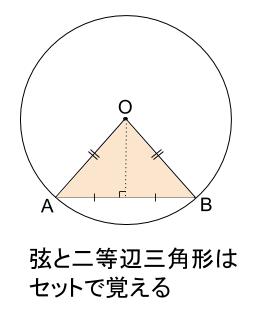
すべての辺の長さと角度が同じである三角形が正三角形です。二等辺三角形の底辺と三平方の定理の関係二等辺三角形の底辺の長さは、三平方の定理でも計算可能です。二等辺三角形の底辺の計算は簡単。

ただ、図をみると合同になる2つの三角形は存在しないように思えます。

そこで、2つの図形の性質を理解するようにしましょう。

では、証明の問題をみてみましょう。

二等辺三角形では2つの辺が等しいと同時に、底面にある2つの角度がそれぞれ等しくなります。