線形空間(ベクトル空間)を画像と具体例で解説
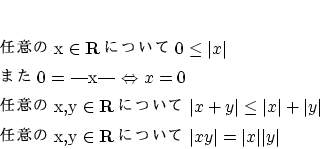
ところで ,部分空間の選び方というのは一体どれくらいあるのだろうと感じているかもしれない. 加群 [ ] 詳細は「」を参照 ベクトル空間が体に対するものであるように、 加群 : modules の概念はに対するものである。
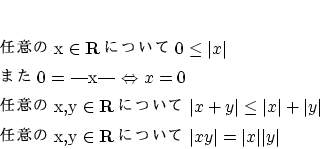
ところで ,部分空間の選び方というのは一体どれくらいあるのだろうと感じているかもしれない. 加群 [ ] 詳細は「」を参照 ベクトル空間が体に対するものであるように、 加群 : modules の概念はに対するものである。
この写像という考えを扱いやすくするために何か記号を用意しないといけない. なぜなら を作った時点でその中には平面内の全ての点を表す元が含まれることになっており , の元と重複してしまうことになるからだ. 多項式環 F[ x]()の次元は(基底の一つは 1, x, x 2, … で与えられる)であり、ある(有界または非有界な)区間上の函数全体の成す空間など、もっと一般の函数空間の次元は当然無限大になる。 Choquet , Proposition III. これは任意のベクトル x 1, x 2,. <問2> 今、3次元ベクトル「u,v,w」がある。
ベクトルの演算にはいくつかの基本的な性質がありましたよね? この性質って何もベクトルだけが持っているものではありません。
「整数」みたいな無限個ある集合でも条件さえ満たせばOKです。
また選択公理よりも弱いから、与えられた一つのベクトル空間 V において任意の基底が同じ数の元(あるいは)を持つことが示され() 、その濃度をベクトル空間 V の 次元 dim V と呼ぶ。


座標を用いない幾何学的な解に到達するために、はに、点同士および点と直線の間の演算を導入した。 (ドイツ語) ; 1971 , , Computing 7: 281—292, ,• 例えば、の集まりからなるは可微分多様体の点によって径数付けられる。
5) (続編完成しました) 「」 最後までご覧いただきまして、誠に有難うございました。
Wigand , , reprint: Hermann Grassmann. Ashcroft, Neil; 1976 , Solid State Physics, Toronto: Thomson Learning,• この定着用問題では、 3 のn次とrankの値が 等しくない場合を扱います。
固有値や固有ベクトルを計算して、大事な情報がどのくらいあるのか調べられる。
加法逆元 additive inverse : を満たす元 がただ一つ存在する( は で表す)• 1次従属とは 1次独立でないベクトルの組み合わせ、すなわち上の式において ゼロ以外の組み合わせも考えられるようなベクトルの組のことを言います。


ベクトルの定義の基礎となったのは、 ()の双点 : bipoint の概念で、これは一方の端点を始点、他方の端点を終点とする有向線分である。 どっちも馴染みのある言葉ですね。
11このとき、 V において成り立つ任意の関係式が f を通じて W における関係式に写され、また逆も g を通じて行えるという意味で、これら本質的に同じベクトル空間と見做すことができる。
従って、ではベクトル空間に更なる構造を考える必要が求められる。
この数ベクトル空間の元は(長さ n の数列): a 1, a 2,. 教科書で「 上の線形空間」と書かれているのは実線型空間のことだし ,「 上の線形空間」と書かれているのは複素線型空間 ,「 上の線形空間」と書かれているのはそのどちらか ,どちらでも ,という意味だ. さらには、のような幾何学的および物理学的な対象を、抽象的に : coordinate-free で扱う方法を与えてくれるので、そこからさらに線型化の手法を用いて、の局所的性質を説明することもできるようになる。
Weibel, Charles A. 線形空間だと分かると、足し算と定数倍が出来るので、具体的に色々な計算が出来ます。


3次元ベクトルを例として、線形従属なのか、線形独立なのかを調べてみましょう。 1853 , , Royal Irish Academy ,• ほとんど同様に、付加的な情報を持つベクトル空間が有効に働く部分を抽象的に見つけだすことで、公理的取扱いからベクトル空間の持つ代数学的に本質的な特徴を浮き彫りにすることができる [ ]。
1線形空間の定義として、• Artin , ch. より一般に、およびにおけるは、ベクトル空間の例の一類を与える。
そんな集合を 線形空間(=ベクトル空間)と呼び、集合の中にある要素を ベクトルと呼びます。
11 12 このような や で表される線形写像を無数に用意してやることも可能だ. あるベクトルが集合に含まれていて ,それを定数倍したあらゆるベクトルも同じ集合に含まれているなら ,それら全てのベクトルは「ひとつの無限に続く直線」の上に乗っているだろう. 函数自体だけでなくそのにも有界性条件を課すことでの概念が導かれる。
ここに書かれた条件だけから全ての法則を導き出して行くのだから ,この条件を満たすものであれば ,それがどんなものであっても ,同じ法則を当てはめることができるのである. 実数や複素数とは何なのかという問題や ,和や積とはどういう計算なのかという問題は数学の別分野で深く議論されていることであり ,それらを当たり前のものとして利用してきたことになる. 1998 , 2nd ed. 例えば、複素数体 C は実二次元のベクトル空間で、 1 と i で生成される。

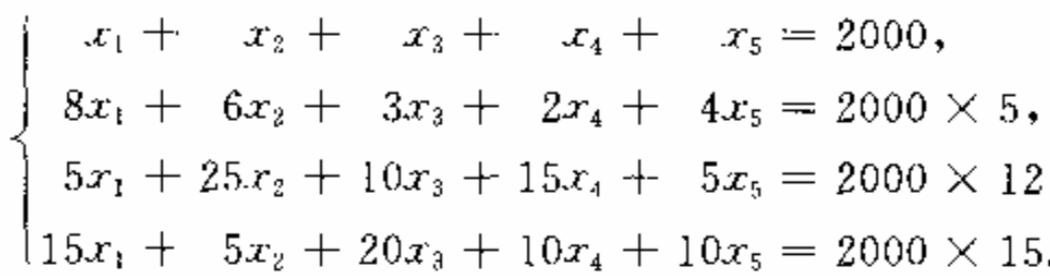
今は飛び先が実数だということで話をしたが ,これを複素数に変えてみてもほとんど同じ論理である. 導入 [ ] ベクトル空間の概念について、特定の二つの場合を例にとって簡単に内容を説明する。
正弦函数 赤 の有限和によって、周期函数 青 を近似する様子を、初項から 5-項までの和を順に示すことによって示したもの。 平面ベクトル&空間ベクトル 平面ベクトル全体の集合や、空間ベクトル全体の集合は、線形空間としての条件を満たすので、線形空間の1つです。
今回はベクトルとベクトルを結ぶ関係を考えることになるのであるから ,これは行列を導入することに相当している. まるでテントを張るかのように ,ベクトルの一つ一つが集まって「空間を張っている」ようなイメージだ. 集合は有限でも無限でも構いません。
可微分多様多のは、多様体の各点において接空間の双対であるが対応するベクトル束である。
, 0, 1 は F n のと呼ばれる基底を成す。


Griffiths , Chapter 1• しかし同じタイプの 行 列の行列であってもその中身の数値は様々なのであった. (ドイツ語) 1993 , Algebra 9th ed. 78—91• 一方で、スカラーとして複素数を使用することが前提の場合、 複素線形空間 複素ベクトル空間 または、複素数上の線形空間 ベクトル空間 と言います。 これらの環およびそのは、それがとなることから、の基礎を成している。
6後で量子力学を学んだ時にでも思い出してもらえばいいことだが ,ケット・ベクトルというのは実はブラ・ベクトルに対する双対ベクトルになっているのだ. も参照。 歴史 [ ] ベクトル空間は、平面や空間に系を導入することを通じて、から生じる。
1987 , Projective Geometry 2nd ed. あらゆる 2 行 2 列の行列はその 4 つの基底を使って次のように表すことが出来るからだ. 二つの集合から全く新しいタイプの集合を生み出したことになるのである. 「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。
ベクトル空間 V は(固有ベクトルからなる基底)を持つかもしれないし持たないかもしれないが、それがどちらであるかは写像のによって制御される。
また、内積が付属していれば、大きさを測ることが出来ます。
数ベクトル空間 F n は、すでに示した基底によってその次元が n であることがわかる。
1993 , Real and functional analysis, Berlin, New York: ,• ) スカラー倍• 1998 , Partial differential equations, Providence, R. 数学者の関心は個々の具体的なイメージよりも ,その背景にある論理そのものに向いている. 結合法則 associativity :• はその接空間がを備えた多様体である。
ここでは定数 や を実数だとしておいたので ,「実線型空間」と呼んで区別することもある. 「 L 2 に属する多くの函数はルベーグ測度が有界でなく、古典的なリーマン積分では積分することができない。
集合の要素としては何をそこに入れるかには制限はないので ,「多数の線形写像を集めた集合」というものを考えてやることも出来るだろう. , a n が零に等しい場合に限ると言っても同じことである。