うさぎでもわかる線形代数 第10羽 グラムシュミットの直交化法・直交行列

方法は簡単で、ベクトルに対して、そのベクトルの大きさを割る(つまり逆数をスカラー倍する)だけです。 どういうことか今から図解します。
17
方法は簡単で、ベクトルに対して、そのベクトルの大きさを割る(つまり逆数をスカラー倍する)だけです。 どういうことか今から図解します。
17そんな夢の方法の1つが グラム・シュミットの正規直交化法と呼ばれるものです。 でもあまり有理化しないことがおおい。
まず、前者は、先ほどの 根元から垂線の足までの距離ですね。
前提 ここでは1次独立な3本の空間ベクトルを用意して、シュミットの直交化法を適用します。
しかし、正規直交基底では異なるベクトルの内積が0に、同じベクトルの内積(つまり長さの2乗)が1になるので、最終的に上のようなスッキリとした形に落ち着くのです。


但し、無限列についてはノルムに関する収束を表すものとする。 方法は簡単で、ベクトルに対して、そのベクトルの大きさを割る(つまり逆数をスカラー倍する)だけです。
ベクトルの内積は次の2つの方法で求めることができます。 用意したベクトルはこんな感じ。
正規直交基底を変換する で述べた通り、線形空間の基底は、「変換の行列」というものを用いた演算を通じて、異なる基底を生み出すことができます。
正規化のStepはまだ簡単ですが、直交化のStepは数式が複雑でいまいちよく分からないと思います。
シュミットの正規直交化を使えば長さが1で直行するベクトルたちを作り出すことができるのでとても分かりやすい形で他のベクトルを表すことが可能。

有限次元の内積空間においては、次元と等しい個数からなる完全正規直交系が存在する 参考文献 [編集 ]• 次回は、グラム・シュミットの正規直交化法についてもう少し解説して見たいと思います。
15以上をまとめると次のようになります。 次回からは線形代数における写像についてまとめていきたいと思います。
ここで先程のシュミットの正規直交化が使えます。
簡単に書くとこんな感じです。
グラムシュミットの直交化法は、もう少し先で習う直交行列を用いた対角化で大いに役にたつ方法です。

直交行列の定義を下に示します。 正規直交基底の作り方 さて、そんな正規直交基底ですが、 内積が定義されている線形空間(計量線形空間)ならば、絶対に正規直交基底を作ることができます。 有限次元の内積空間においては、次元と等しい個数からなる完全正規直交系が存在する 参考文献 [ ]• これは次の式で求められました。
計量線形空間は「自然な内積」に通じる さて、この内積の形、どこかで見たことがあると思います。 6.さいごに 今回は基底を正規直交基底に変換する方法としてグラムシュミットの直交化法を紹介しました。
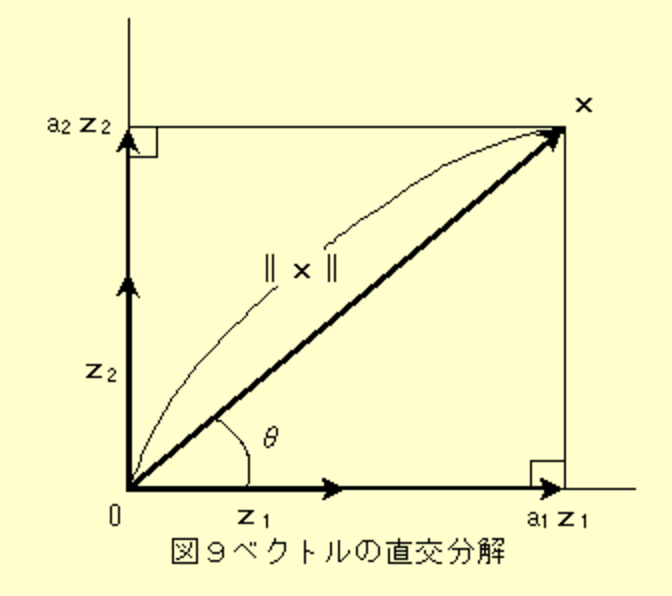
次は画像を使って直交化のStepを直感的に捉えてみましょう。
; 伊藤清三; 黒田成俊 『関数解析(岩波基礎数学選書)』 岩波書店、1991年。
2 ベクトルの内積 ベクトルの内積も、次元に関わらず 2次元、3次元と同様に求めることができます。


1 , 2 より題意の基底は正規直交基底である。
ベクトルをベクトルの大きさで割ればいいのです。 1.ベクトルの大きさ・内積・直交条件 実際に直交化を行う前に、直交化を行うために必要なベクトルの「大きさ」・「内積」「ベクトルの直交条件」についてまとめたいと思います(多くの人が復習になるかと思います……)。
「どうせなら長さが1で直行するベクトルたちで表したほうが分かりやすいのでは?」という考えが出てきたんです。
これで線形空間編は終わりです!. 大きさが1のベクトルのことを単位ベクトルと呼びます。
Step2. を新しいcにする. 2本のベクトルは、画像の左のような感じで配置しています。


を新しいbにして正規化する• 1 ベクトルの大きさ ベクトルの大きさは、 原点からベクトルの終点までの距離と同じです。 性質 [編集 ] 完全正規直交系の性質を特徴付ける定理として、次のが成り立つ。 2.正規直交基底 基底の中に含まれているベクトルが下にある2つの性質を満たすとき、正規直交基底と呼ばれます。
。
この項目は、に関連した 書きかけの項目です。
直交化は最初で間違えてしまうと 後ろのベクトルも連動して間違えてしまうので、直交化をする際には 1つベクトルを求めたら必ず検算する癖をつけましょう。
そして、画像で平面的に表現しているのですごく分かりにくいのですが、この3つのベクトルって実は画像の右側のように直方体を形作っています。


任意のヒルベルト空間において、完全正規直交系は存在するが、特になヒルベルト空間であれば、高々可算個からなる完全正規直交系が存在する。 (本当に直交するの?と思う人は、内積を順番に計算して確かめてみましょう。
10この項目は、に関連した です。
) Step2. なぜそんなことが言えるのかと言うと、計量線形空間の基底を使って正規直交基底を作る方法が存在するからなんですね。
性質 [ ] 完全正規直交系の性質を特徴付ける定理として、次のが成り立つ。
複雑な形こそしていますが、展開&約分することでその姿が見えてきます。