平面図形

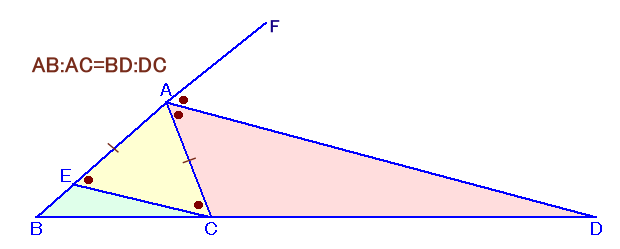
ただし、三角定規の角のようにきれいに表現できるとは限りません。 三角形の面積比の練習問題 問題 それでは、実際に問題を解いていきましょう! 問題1 次の図のように、点Aから引いた線と辺BCの交点をDとする。
8

ただし、三角定規の角のようにきれいに表現できるとは限りません。 三角形の面積比の練習問題 問題 それでは、実際に問題を解いていきましょう! 問題1 次の図のように、点Aから引いた線と辺BCの交点をDとする。
8教材と会員番号&パスワード到着後よりご利用いただけます。
少し練習すればすぐに使える様になりますが、暗記が好きな人は表を覚えても良いです。
垂心の存在の3通りの証明• ヒポクラテスの定理とその証明• 2月号以降を継続されない場合は、支払い期間にかかわらず「毎月払い」1ヵ月分の受講費のお支払いとなります。
頑張る中学生を かめきち先生は応援しています。

Kiepertの定理とその証明• 等周問題に関連する高校数学の問題• この辺の比になる直角三角形の角度は、• 三角形の中心(36個)を図示してみた• まとめ 三角形と平行線の線分の比について まとめます。 直角三角形において三平方の定理が成り立つので、 三角比の重要な関係(公式)がいくつか得られます。 三角比に慣れるまでは、このような方法も知っておくと便利ですね! 三角比の拡張 さらに、もう少し三角比の考え方を拡張してみます。
6小6・4月号以降に「チャレンジパッド2」をお届けした場合、以前にお届けした「チャレンジパッド2」をご利用ください。
ぜひご入会をご検討ください(8月号のお届けは通常3日前後でお届け予定ですが、配送状況によって2-3日遅れる可能性があります点は、あらかじめご了承ください)。
三角形の決定条件と自由度• 余弦定理 の内容と、代表的な使い方を説明していきます。
チェバの定理の3通りの証明• 45の直角三角形• まだ不安が残るという人は、引き続き練習問題に取り組んでいきましょう。

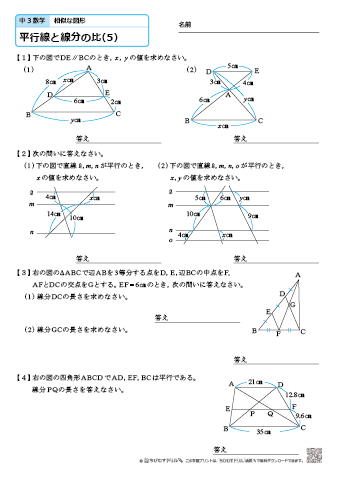
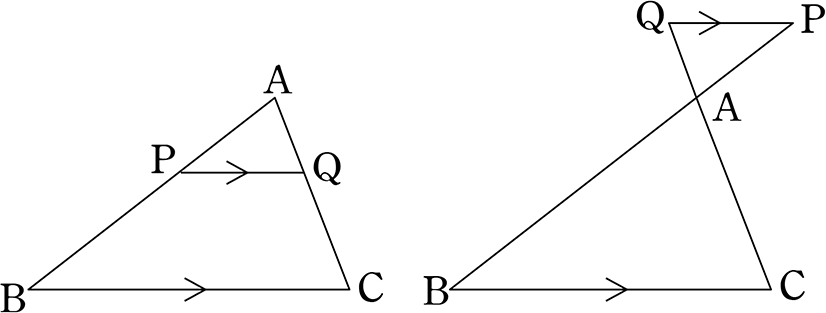
ケージーの定理とその証明• 2つの円の位置関係• もちろん、万が一忘れてしまっても、先ほど説明した 三平方の定理ですぐに導き出せるので、あわてないでくださいね。 平方根の長さを作図する2通りの方法• 振込用紙・Webサービス(含む)利用の 会員番号・パスワードは教材とは別便(郵送)で5日前後で後送します。 この直線は,どのように交わっても,平行線によって一定の比に分けられます。
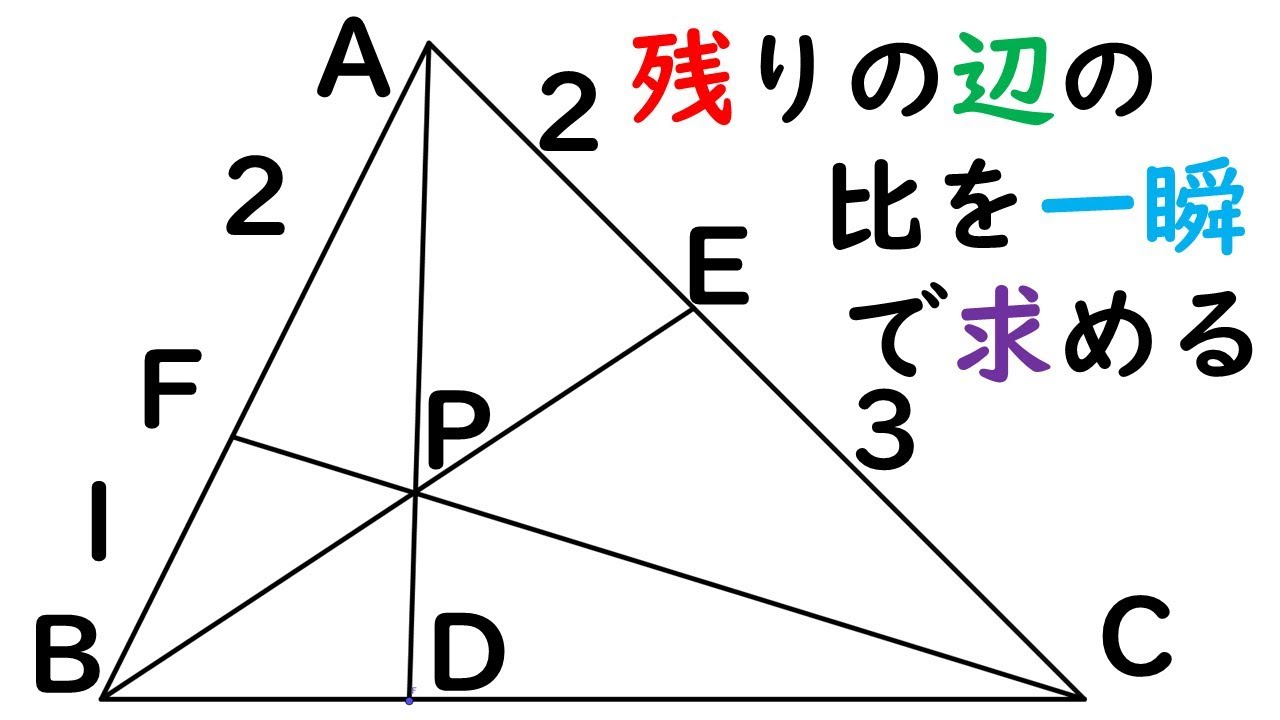
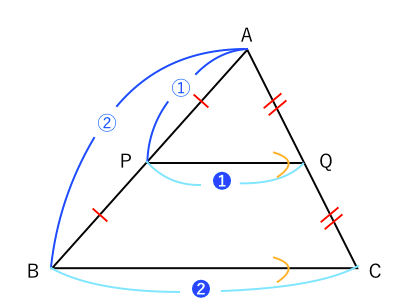
また, A M AM A M の中点が P P P , A N AN A N の中点が Q Q Q となるように M , N M,N M , N を取る。
また,相似な場合は有名な体積比の公式(1:相似比の3乗)となります。
これらの表記は、正弦定理・余弦定理で頻繁に登場するものです。
対応する辺の比はどれも同じだということまで覚えていれば完ぺきです。
先ずはよく知っている余弦定理です。
角の二等分線と線分の比• 図形の美しい3つの定理〜逆数の和〜• またこの逆も成り立ちます。
補足1:三角形が一意に決まらない理由 今回の問題では、 三角形の形状が一意に決定できませんでした。
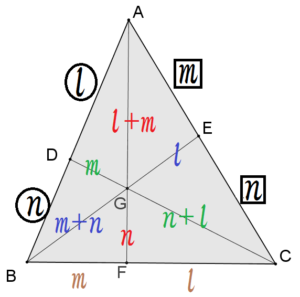
三角形ABCにおいて,辺AB,AC上に,それぞれ点D,Eをとります。

表にしておきますが、三角形を書いて比を見るようにしておいた方がいいです。 「3 4 5 の直角三角形」 最後の直角三角形の辺の比は、 3 : 4: 5 だよ。 この考え方は後で紹介する三角比の相互関係を求めるときにも利用するので、単位円の書き方とともに理解しておいてください。
14フランク・モーリーの定理の証明• DEとBCが平行ならば,各辺は点によって一定の比に分けられます。 調和点列の様々な定義と具体例• 九点円の定理の証明と諸性質• iPadシリーズの会員特別優待販売もご用意しています。
最後まで読んでいただき ありがとうございました。
高さの比も相似比と同様に1:2ですね。
この直角三角形の2辺の長さを比べてみると、 6: 8 つまり、 3: 4 になってるよね?? ってことは、この三角形は3: 4: 5の直角三角形ってことがわかるね。
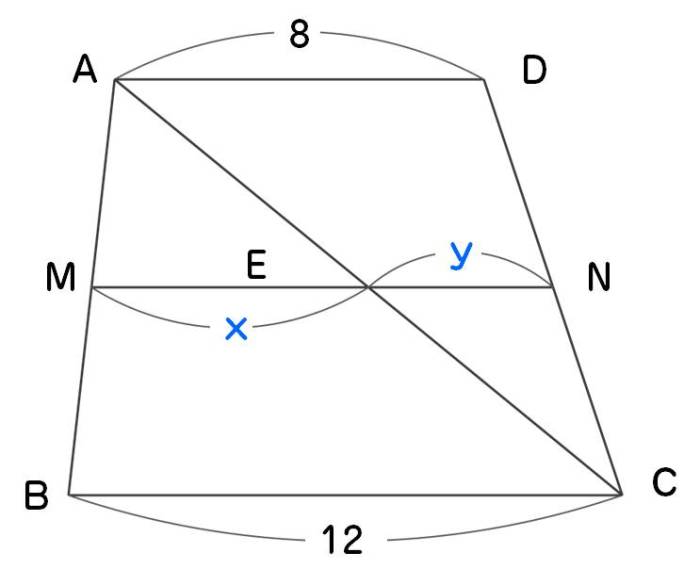
お住まいの地域・受付時間によって配送状況が異なります。 単なる文字式計算なので自分でやっておいて下さい。 【確認】 四角形ABCDで、P,Rはそれぞれ辺AD, BCの中点、Q,Sはそれぞれ対角線BD,ACの中点である。
12(有理数まではなんとか使えますが、時間がかかりそうな場合は避けます。 多数のお客様にご希望いただいた場合、3日前後でのお届けになります。
トレミーの定理とその3通りの証明,応用例• このタイプの直角三角形をどこかでみたことある?? 実はこれ、三角定規の直角三角形のうちの長い方だね。
射影平面の3通りの定義• また、商品発送等で個人情報の取り扱いを業務委託しますが、厳重に委託先を管理・指導します。
三角比の定義の覚え方 三角比の値を覚える方法として、筆記体を利用した覚え方があります。
そのため、通常の比の計算より少しむずかしく感じるかもしれません。
この公式の頻出応用例として,• 円に内接する三角形の面積の最大値• 以上2つの頻出系の合体技の例としてと2つ目の証明を挙げておきます。 それじゃあ、また ぺーたー. 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。
ルモアーヌ点(類似重心)とその性質• ポイント 正弦定理の公式のうち の部分に着目します。
正弦定理は、その名の通り正弦 sin に関する定理で、次のようなものです。
リサージュ曲線の定義とそれに関連する話. 中学数学の問題では3秒に一回ぐらい使う直角三角形の辺の比だから、 確実に覚えておこう。

三角比の拡張 三角比の定義は先にお伝えしました直角三角形を用いたものと、 原点を中心とする円を用いたものがあります。
ADに対する平行線ECを引いてあります。
余弦定理 余弦定理には2種類あります。
中点連結定理• 接弦定理とその逆の証明など• 等角共役点とその証明• (覚えなくても良いですけど、知っておいて損はありません。
(株)ベネッセコーポレーション CPO(個人情報保護最高責任者) 最速翌日お届け! 3日以内にスピード配送中! 最速お届けご希望の場合はWebまたはお電話で! 地域/受付時間 ~13時まで 13時以降~ 北海道・東北・沖縄県・ その他一部の地域 2日前後 3日前後 上記以外の地域 翌日 2~3日前後 最速お届けの受付は月曜~土曜のみです。