球対称な質量分布が作る重力ポテンシャル

回転楕円体の性質を考えれば、正規重力の値も緯度によってのみ決まり、経度にはよらない。
14a , b , c ではそれぞれどのようなことを行っているのでしょうか?解説をお願いします。 例えば原子では、正の電荷をもつ原子核の周囲に同じ電荷分だけの電子が集まります。
。
積分 ここで積分についておおざっぱに説明します。
「重力による位置エネルギー 地表近く 」を例として実際に積分してみましょう。

このように物体の「位置」によって決まるエネルギーを「位置エネルギー」といいます。
地球の半径を R とします。
276-279,• ですから両者を比べることはできません。
分子A、分子B の二つを考えた時、 Aの原子核-Bの原子核間、およびAの電子-Bの電子間の反発力 に比べ、 Aの原子核-Bの電子間 、およびAの電子-Bの原子核間の引力 の方が少し強い。
位置 にある質量 の質点が位置 に作る重力ポテンシャル は で与えられます(点を基準とする)。

GP はジオイドと直交してないから、「高さ」にならない• 重力ポテンシャル(: gravitational potential)とは、において、ある点における単位あたりのによるのことである。 でも水が下に向かって落ちるのは何で? いい質問です.それは,水が重力を受けているからで,重力の働く向きが下向きだからです.いま言いましたポテンシャルというのは,もうちょっと正確にいうと重力のポテンシャルです.重力のことは知っていますね? あー. 知ってるんですか,知らないんですか.どっちなんですか? 知ってる(聞いたことはある). 重力というのは,高い方から低い方に向かって働きます.上にあるものは下に落ちるでしょう? うんうん.上り詰めると後は堕落するか引きずり降ろされるかどっちかだからね. なんかヤな表現ですね. 重力以外にもポテンシャルはあるん? あります.重力の他にも「クーロン力」や「磁力」などのポテンシャルが存在します. はあ.「クーロンリョク」ヤ「ジリョク」ナドノポテンシャルガソンザイシマスカー. つまりですね,重力のポテンシャルがあるとそのポテンシャルが高い方から低い方に力を受けます.同じように,クーロン力のポテンシャルがあるとクーロン力のポテンシャルが高い方から低い方に力を受けます.磁力の場合も同様です. クーロンとか磁力とかはよくわかんないけど,まあいいや. そうですね.ポテンシャルの高い方から低い方に力を受ける,ということだけ覚えといてください. ところで,ポテンシャルを考えるときはどこを基準にとるかが大事です. えー? 滝の例でみたように,ポテンシャルはある点とある点の「差」に意味があります.「崖の上」と「崖の下」,「坂の上」と「坂の下」というふうに. 坂の上といえば,『坂の上の雲』って本を前に読んだよ.でも途中で挫折しちゃった. (無視.)ポテンシャルの大小を考えるとき,どこを基準とするかは自由です.普通は無限遠でゼロになるように基準点をとることが多いです. 眠くなってきちゃった. そうですね.ポテンシャルに興味が持てたら,本など読んで詳しく勉強してみると良いですね.では本日はこれにて. どんな本を読んだらいいん? 『坂の上の雲』なら持っているけど,途中で挫…… あ,その話はもう聞いたんでいいです. 冷たっ. ポテンシャルエネルギーについての説明は,力学の本ならどんな本でも載っていますよ.『 』や『 』なんかは分かりやすかったですね.. これは球体の内側の重力ポテンシャルを与えます: これは で上記の球体外のポテンシャルと連続的につながっています。
7どちらかというとで静電ポテンシャルの計算としてやった記憶の方が強いですが、まぁ全く同じ計算でした。
しかしこれですと、地表付近の物体の位置エネルギーを考えるときにはいいかもしれませんが、他の一般の物体について考えるときは不合理です。
関連項目 [ ]• ポテンシャルエネルギーは r の 1 乗 に反比例します。
となり、静電気力が圧倒的に大きいことがわかります。

今は M と m は定数とみなします。 10 c が、平板上の点に及ぼす引力である。 ある物体に 力 F がかかっている場の中で、 その物体を力に逆らう方向に、距離 x だけ移動させると その物体はエネルギー Fx を得ると考えてよいでしょう。
この補正を「単純ブーゲー補正」という。
第1項は に比例しているので、これは のポテンシャルに等しいことが分かります。
R より近い距離では位置エネルギーが負になり、 R より遠い距離では位置エネルギーが正になるなんて面倒です。
これを上式に代入します。

数学では、重力ポテンシャルは ()とも呼ばれ、の研究において基本的である。 3章 地球楕円体 地球の形は回転楕円体に近いはずだから、重力から地球の形を決める際にも、回転楕円体が作る重力を基準に考えるのがよい。 しかしこれら質量の小さいもの同士の間に働く重力は非常に小さいので、通常問題になることはありません。
19地球を物体A、地表付近の物体を物体Bとし、物体Aの質量を M 、物体Bの質量を m 、物体Aの半径を R 、地表面から物体Bの距離を h 、万有引力定数を G 、重力加速度を g とします。
どういうことか、以下説明します。
と の大小関係で形が変わるのはちょっと面倒そうだけど。
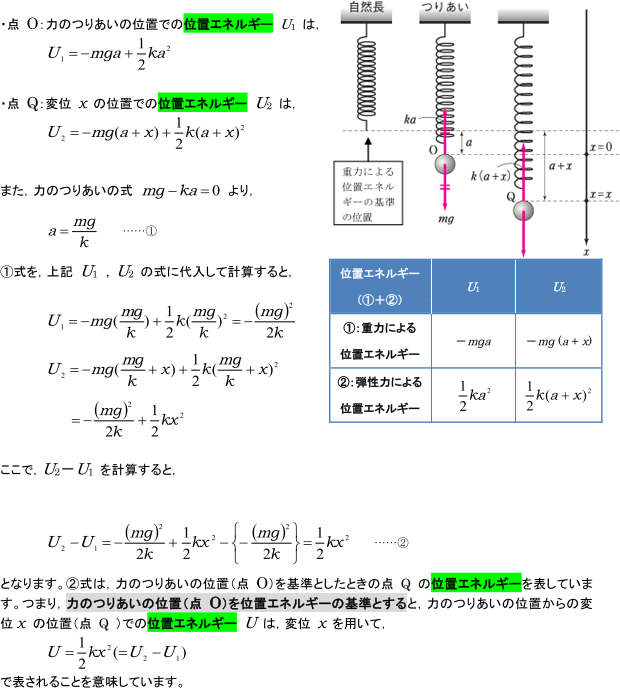
弾性力による位置エネルギーの大きさは、 kx という力を受けながら距離 x だけ移動したときの仕事の大きさです。


球体内に一様分布する質量分布原点を中心とし、半径が の球体内に一様に質量が分布している系を考えましょう。 上式の M に地球の質量、 r に地球の半径を代入すると は g 前項に出てきた重力加速度 になります。 基準位置を工夫する 位置エネルギーというものは主に、2つの地点における位置エネルギーの「差」が問題になるので、基準位置はのです。
h は地表を 0 として、「上」に行く方向を正としています。 保存力が発揮されている空間においては、位置だけで決まるエネルギーがあるとみなせます。
5章 重力を測定する目的の1つは、地下の構造やその時間変化を知ることにある。
77-79• リフシッツ『場の古典論』東京図書〈理論物理学教程〉, 1978年. 質量分布は以下で与えられます: 最後の式は階段関数(Heaviside 関数) を使って書いてみただけで特に深い意味はありません(この はの角度とは関係ないよ)。
力とエネルギーの符号について ここで、符号について説明しておきましょう。